Weekend Mathematics／問題／問題25

２５．１９９９年の問題

１９９９！を十進法で表すとき、末尾に何個の０が並ぶでしょうか？

(ただし、Ｎ！＝Ｎ(Ｎ−１)(Ｎ−２)・・・３・２・１です。)

解答・その１

（ペンネ−ム：ヤマさん）

p個の０が並ぶとおく。
このとき １９９９！＝ａｘ１０^ｐ （ａは１０で割り切れない整数） とおける。
１０^ｐ＝２^ｐｘ５^ｐ より、 １９９９！がいくつの２^ｐｘ５^ｐ を持つかを調べればよい。
１〜１９９９において５の約数を持つ整数の方が少ないことは明らかであるから、 ５の約数の個数を求める。
１〜１９９９の中で、 ５、２５、１２５、６２５で割り切れる数の個数はそれぞれ、
５・・・３９９
２５・・・７９
１２５・・・１５
６２５・・・３
となる。
ここで、２５・・・７９は、２５で割り切れる数が５で割り切れる数 にはない新たな５の約数を７９個持つことを表すから、 上記の個数には重複がないと言える。
よって１９９９！がもつ５の約数の個数は、
３９９＋７９＋１５＋３＝４９６
ゆえに１９９９！は、２^４９６ｘ５^４９６を約数に持つ。
だから、１９９９！＝ａｘ１０^４９６となり、末尾には０が４９６個並ぶ。

解答・その２

（ペンネ−ム：２丁目の山田）

ｎ個０が並ぶ⇔10ⁿで割れる
で、ここでは
⇔５ⁿで割れる
で、1999!何回５でわれるかで
[1999/5]+[1999/25]+[1999/125]+[1999/625]=399+79+15+3=496
[x]はxを越えない最大の整数

解答・その３

（ペンネ−ム：kiyo）

１９９９！のなかに５の素因数がいくらあるか調べる。
１９９９÷５＝３９９．．．４
１９９９÷２５＝７９．．．２４
１９９９÷１２５＝１５．．．１２４
１９９９÷６２５＝３．．．１２４
３９９＋７９＋１５＋３＝４９６
２の素因数はそれ以上であるから、末尾の０の個数は４９６個となる。
答え　４９６個。

解答・その４

（ペンネ−ム：みや）

１９９９！が１０の何乗で割り切れるかということだから ２×５の何乗かを考える。
２についてはたくさんあるから、 １９９９！に（×５）がいくつ含まれているかを考える。
１９９９以下の５の倍数は３９９個（１９９９÷５）
１９９９以下の５の２乗の倍数は７９個（１９９９÷２５）
１９９９以下の５の３乗の倍数は１５個（１９９９÷１２５）
１９９９以下の５の４乗の倍数は３個（１９９９÷６２５）
１９９９！に含まれる（×５）の個数は３９９＋７９＋１５＋３＝４９６
よって（２×５）が４９６個含まれている。
答え ４９６

解答・その５

（ペンネ−ム：ｙｕｕちゃん ）

１０^ｎ＝(２×５)^ｎ＝(２^ｎ)×(５^ｎ)となります
１９９９！＝１９９９×１９９８×１９９７×・・・・・・×３×２×１
１９９９！の式の中で、２で割れるものは、
１９９８、１９９６、・・・・、４、２であり、
除した商も同様に考えると、
（９９９＋４９９＋２４９＋１２４＋６２＋３１＋１５＋７＋３＋１）となります
また、同様に５で割れるものは１９９５、１９９０、・・・・、１０、５であり、
（３９９＋７９＋１５＋３）となります
これらより

　１９９９！
＝(２(９９９＋４９９＋２４９＋１２４＋６２＋３１＋１５＋７＋３＋１))×(５(３９９＋７９＋１５＋３))×・・・・
＝(２(３９９＋７９＋１５＋３))×(５(３９９＋７９＋１５＋３))×(２(９９９＋４９９＋２４９＋１２４＋６２＋３１＋１５＋７＋３＋１)−(３９９＋７９＋１５＋３))×・・・・
＝(１０(３９９＋７９＋１５＋３))×・・・・・

解答・その６

（ペンネ−ム：まめ ）

１９９９！を素因数分解した場合に、 ２と５が一組あるごとに、末尾に１０が増えていきます。
明らかに、２よりも５の方が個数が少ないですから、 いくつ５があるかを数えれば、それが答えです。
まず、１９９９を５で割って、 １９９９以下の５の倍数の個数を求めてみます。
１９９９÷５＝３９９・・・４
ですから、全部で３９９個あります。
しかし、５の数はこれだけではありません。
それは、２５や、１２５など、５のｎ乗で表されるものがあるからです。
５の２乗である２５の、１９９９以下の倍数は、
１９９９÷２５＝７９・・・２４
というわけで７９個。 これでさらに５の数は７９個増えます。
また、５の３乗である１２５の、１９９９以下の倍数は、
１９９９÷１２５＝１５・・・１２４
というわけで１５個。これでさらに５の数は１５個増えます。
最後に、５の４乗である６２５の、１９９９以下の倍数は、
１９９９÷６２５＝３・・・１２４
というわけで３個。これでさらに５の数は３個増えます。
以上の考察から、１９９９！を素因数に分解した場合にでてくる５の個数は、
３９９＋７９＋１５＋３＝４９６
となります。 これが、１９９９！を計算した場合に、末尾に並ぶ０の個数です。

図で描くともう少し分かりやすくなりそうです。
下のように、５がでてくるたびに、●をつけていきます。

　　　　　　　　５　　　　●
　　　　　　　１０　　　　●
　　　　　　　１５　　　　●
　　　　　　　２０　　　　●
　　　　　　　２５　　　　●　　　　●
　　　　　　　　・　
　　　　　　　　・
　　　　　　　５０　　　　●　　　　●
　　　　　　　　・
　　　　　　　　．
　　　　　　　７５　　　　●　　　　●
　　　　　　　　・
　　　　　　　　・
　　　　　　１２５　　　　●　　　　●　　　　●
　　　　　　　　・
　　　　　　　　・
　　　　　　２５０　　　　●　　　　●　　　　●
　　　　　　　　・
　　　　　　　　・
　　　　　　６２５　　　　●　　　　●　　　　●　　　　●
　　　　　　　　・
　　　　　　　　・
　　　　　１２５０　　　　●　　　　●　　　　●　　　　●
　　　　　　　　・
　　　　　　　　・
　　　　　１８７５　　　　●　　　　●　　　　●　　　　●
　　　　　　　　・
　　　　　　　　・
　　　　　１９９９　　　　−　　　　−　　　　−　　　　−
−−−−−−−−−−−−−−−−−−−−−−−−−−−
　　　　　　　　　　　　３９９　　　７９　　　　１５　　　　３

解答・その７

（浜田　明巳 ）

答は４９６個です。
ようするに１９９９！を素因数分解したときに、 何個の５が含まれているかを求めればよいわけです。
そのために、５から１９９５までの５の倍数の中で、 何個の５が含まれているかを、 次のVISUAL BASICのプログラムで求めてみました。

Option Explicit
Private Sub Command1_Click()
    '1999!を十進法で表すとき，末尾に何個の０が並ぶでしょうか？
    Dim kotae, j, jj As Integer
    kotae = 0
    For j = 5 To 1995 Step 5
      jj = j
      Do While jj Mod 5 = 0
        jj = jj \ 5
        kotae = kotae + 1
      Loop
    Next
    Picture1.Print "答＝"; kotae
End Sub
Private Sub Command2_Click()
    End
End Sub

解答・その８

（ペンネ−ム：水の流れ ）

解答　１０＝２×５より、１９９９！の中に１０の倍数は何個あるかは、 ５の倍数が何個あるかになります。 だから、
１から１９９９までに５の倍数がａ個で、
１から１９９９までに５^２＝２５の倍数がｂ個で、
１から１９９９までに５^３＝１２５の倍数がｃ個で、
１から１９９９までに５^４＝６２５の倍数がｄ個あるとします。 よって、

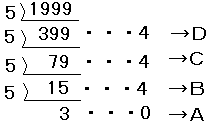
したがって、＝３９９＋７９＋１５＋３＝４９６（個）・・・（答え）
または、ガウス記号を［　　　］を使って、

ａ＋ｂ＋ｃ＋ｄ ＝［1999/5］＋［1999/25］＋［1999/125］＋［1999/625］
               ＝３９９＋７９＋１５＋３＝４９６（個）・・・（答え）

定理１
ｎ！に含まれる素数ｐのすべての個数をｎ(ｐ)とおくと、

ｎ(ｐ) ＝［ｎ/ｐ］＋［ｎ/ｐ2］＋［ｎ/ｐ3］＋［ｎ/ｐ4］＋・・・
　　　 ＝ａ＋ｂ＋ｃ＋ｄ＋・・・  　　　である。

そこで、自然数ｎをｐ進法で表して、これを用いて別の方法で解きます。
ｎ＝Ａｐ^α＋Ｂｐ^(α−1) ＋Ｃｐ^(α−2)＋ Ｄｐ^(α−3)＋・・・＋Ｇｐ＋Ｈ
ただし、Ａ≠０，０≦Ａ，Ｂ，Ｃ，Ｄ，・・・，Ｇ，Ｈ＜ ｐ とする。
また、Ｈは(α+1)番目とします。
すなわち、表記として、ｎ・・・（十進法）→ＡＢＣＤ・・・ＧＨ　＜ｐ進法＞
ここで、
ｎ／ｐ＝Ａｐ^(α−1) ＋Ｂｐ^(α−2)＋Ｃｐ^(α−3)＋・・・＋Ｇ＋Ｈ／ｐ
ですから、
ａ＝［ｎ/ｐ］＝Ａｐ^(α−1)＋Ｂｐ^(α−2)＋Ｃｐ^(α−3)＋・・・＋Ｇ
ｂ＝［ａ/ｐ］＝Ａｐ^(α−2)＋Ｂｐ^(α−3)＋・・・＋Ｆ
　　・・・・・・・・・・・・・・・・・・・
ｇ＝［ｆ/ｐ］＝Ａｐ＋Ｂ
ｈ＝［ｇ/ｐ］＝Ａ
したがって、これらα個を全部加えて

 ｎ(ｐ)＝ａ＋ｂ＋ｃ＋ｄ＋・・・＋ｇ＋ｈ  
　　　 ＝Ａ×（ｐα−１）/(ｐ−１)＋Ｂ×｛ｐ(α−1)−１｝/(ｐ−１)＋・・・＋Ｇ

  ｎ(ｐ)×（ｐ−１）
＝｛Ａｐα＋Ｂｐ(α−1) ＋Ｃｐ(α−2)＋Ｄｐ(α−3)＋・・・＋Ｇｐ｝−（Ａ＋Ｂ＋Ｃ＋・・・＋Ｇ）　　　　
＝｛Ａｐα＋Ｂｐ(α−1) ＋Ｃｐ(α−2)＋Ｄｐ(α−3)＋・・・＋Ｇｐ＋Ｈ｝−（Ａ＋Ｂ＋Ｃ＋・・・＋Ｇ＋Ｈ）
＝ｎ−（Ａ＋Ｂ＋Ｃ＋・・・＋Ｇ＋Ｈ）

定理２
ｎ！に含まれる素数ｐのすべての個数をｎ(ｐ)とおいて、
ｎ＝Ａｐ^α＋Ｂｐ^(α−1) ＋Ｃｐ^(α−2)＋Ｄｐ^(α−3)＋・・・＋Ｇｐ＋Ｈ
ただし、Ａ≠０，０≦Ａ，Ｂ，Ｃ，Ｄ，・・・，Ｇ，Ｈ＜ ｐ とする。
また、Ｈは(α+1)番目とします。　
　 すなわち、表記として、ｎ・・・（十進法）→ＡＢＣＤ・・・ＧＨ　＜ｐ進法＞
このとき、
ｎ(ｐ) ＝{ｎ−(Ａ＋Ｂ＋Ｃ＋・・・＋Ｇ＋Ｈ)}／(ｐ−１) ・・・（答え）

例　１９９９(10進法)は５進法で３０４４４<5進法>と表せます。
よって、前述の表記によると、
Ａ＝３，Ｂ＝０，Ｃ＝４，Ｄ＝４，Ｅ＝４　だから、
求める個数は
{１９９９−(３＋０＋４＋４＋４)}／(５−１)＝４９６　（答え）

まとめ

今回は、因数５の個数を数える、という問題でした。
そのためには、５で次々と割っていくわけですから、 １０進法表示されている１９９９を５進法表示に直す時の作業と全く同じです。

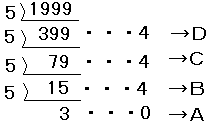
この時に、５で割った商を次々に足していって、４９６という答えを出したわけです。
それに対して１９９９を５進法表示に直す時は、商ではなく余りに注目して３０４４４と表記します。
その関連を「水の流れ」さんが見事に解明してくださいました。

関連した内容が コロキウム室のNO.297と NO.298と NO.315にあります。

戻る