
Weekend Mathematics�^�R���L�E�����^1998.7�`12�^NO.24
NO.184 �@�@�@ 11/1 �@�@���̗��� �@�@�@ 1998�{���̖��i�P�j
���̓��e�ł��B

NO.185 �@�@�@ 11/1 �@�@Hungry Bear �@�@�@ Alphabet�̖��i�P�j ��� �q���g�F
���́��ɓ���͉̂��ł��傤
(�ꕔ����11/1�17:40)

NO.186 �@�@�@ 11/2 �@�@Junko �@�@�@ �W���|�X�̖��i�R�j �����T���{�X���i�������A�����O�C�����O�Ȃ鐮���j�����̂悤�ɕό`���܂��B
�����T���{�X��
�@���T(���{��)�{�S��
�������A�����O�C�����O�Ȃ鐮��
���������T�̏�]�ށi�T�Ŋ������Ƃ��̗]��j�ŕ����܂��B
���̒l�͂��ꂼ��T�̏�]�ɍ��킹���Œ�̐���ݒ肵�Ă��܂��B
�ł�����A������菬�������ɂ��ẮA
���Ƃ����ǂ��Ƃ��Ă��s�\�ł���Ƃ������Ƃ������܂��B
�����O�Ƃ���B
�����T���ƂȂ�̂ŁA���ɓK���Ȑ���^���邱�ƂŁA���ׂĂn�j�B
�����S�Ƃ���B
�����T(�S�{��)�{�P�U
�@���R�U�{�T��
�ƂȂ�̂ŁA���ɓK���Ȑ���^���邱�ƂŁA�R�U�ȏ�̐��ɂ��Ă͂n�j�B
�����R�Ƃ���B
�����T(�R�{��)�{�P�Q
�@���Q�V�{�T��
�ƂȂ�̂ŁA���ɓK���Ȑ���^���邱�ƂŁA�Q�V�ȏ�̐��ɂ��Ă͂n�j�B
�����Q�Ƃ���B
�����T(�Q�{��)�{�W
�@���P�W�{�T��
�ƂȂ�̂ŁA���ɓK���Ȑ���^���邱�ƂŁA�P�W�ȏ�̐��ɂ��Ă͂n�j�B
�����P�Ƃ���B
�����T(�P�{��)�{�S
�@���X�{�T��
�ƂȂ�̂ŁA���ɓK���Ȑ���^���邱�ƂŁA�X�ȏ�̐��ɂ��Ă͂n�j�B
�ȏ�̂��Ƃ���A�\������Ă݂܂����B
| �P | �Q | �R | �S | �T |
| �U | �V | �W | �X | �P�O |
| �P�P | �P�Q | �P�R | �P�S | �P�T |
| �P�U | �P�V | �P�W | �P�X | �Q�O |
| �Q�P | �Q�Q | �Q�R | �Q�S | �Q�T |
| �Q�U | �Q�V | �Q�W | �Q�X | �R�O |
| �R�P | �R�Q | �R�R | �R�S | �R�T |
| �R�U | �R�V | �R�W | �R�X | �S�O |
| �E�E�E |
�ԂɂȂ��Ă���̂��A
�����T���{�X���i�������A�����O�C�����O�Ȃ鐮���j��
�\�����Ƃł��鐮���ł��B�O�p�`�Ɏc��̂��������낢�ł��ˁB
�]���āA�����\�����Ƃ̂ł��Ȃ��ő�̐����́u�R�P�v
�ł��邱�Ƃ��킩��܂��B

NO.187 �@�@�@ 11/4 �@�@���̗��� �@�@�@ �ŒZ�V���^�C�i�[���i�R�j ���āA�ŒZ�V���^�C�i�[���͂Q���̃A�N������B�ŏ�����Ԃ�
����āA�ł��t���܂��B��܉t�𐅂ŗn�����āA���̒��ɓ���āA
�����グ�܂��B����ƁA�������ł܂��B
�@���ʂ̂S�p�`�A���T�p�`�A���U�p�`�܂ł͎������H�R�m�搶��
�e���r�ŕ��f���Ă��܂����A�i�T�N�O�j
�d�S�͖��W�ł��B�ǂ��̓_�Ō���邩�H���ꂪ�������
�ŒZ�̋����͏o�܂��B���̉��p���S�p�`�A�T�p�`�A�U�p�`��
�Ȃ���܂��B

NO.188 �@�@�@ 11/4 �@�@Junko �@�@�@ ���ϕ����㏸���i�Q�j �S�O�N�ԁA�ψ�ɕ������㏸�����Ƃ��āA
���̕��ϕ����㏸�������Ƃ���ƁA ������umathematica�v�Ōv�Z���܂�����A0.0592537����Əo�܂����B
��5.9%�ł��ˁB
�P�O�~(�P�{��)40���P�O�O
(�P�{��)40���P�O
(�P�{��)���P�O(1/40)
�����P�O(1/40)�|�P

NO.189 �@�@�@ 11/5 �@�@naomi �@�@�@ Alphabet�̖��i�Q�j

NO.190�@�@�@�@ 11/7 �@�@���̗���@�@�ӎO�p�`�̏ؖ��i�R�j
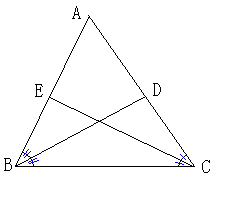
�P�R�Q�Œ�N�������ł��B
���
�O�p�`�`�a�b�ɂ����āA�ڂa�A�ڂb�̂Q��������
�Εӂƌ����_���c�A�d�Ƃ���Ƃ��A
�a�c���b�d�Ȃ�`�a���`�b�ł��邱�Ƃ��ؖ�����B
��
�a�b�����A�b�`�����A�`�a�����Ƃ����B

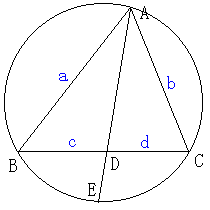
(**)
���p�̂Q�������̒����Ɋւ��āA���̊W�����藧���܂��B
���`�a�b�ɂ����āA�ڂ`�̓��p�̂Q�������ƕӂa�b�Ƃ̌�_
���c�Ƃ���B
���̂Ƃ��A�`�a�����A�`�b�����A�a�c�����A�c�b�����Ƃ����ƁA
�����`�c�̒����́A
�`�c2�������|�����Ƃ�����B
�ؖ�
��̐}�̂悤�ɁA���`�a�b�̊O�ډ~���l���A
�`�c�̉����Ƃ̌�_���d�Ƃ���B
�ڂa�`�d���ڂb�`�c�A�ڂa�d�`���ڂc�b�`���A
�Q�p���������̂ŁA
���a�`�d�䁢�b�`�c
�]���āA�Ή�����ӂ̔䂪���������Ƃɂ��A
�`�a�F�`�c���`�d�F�`�b
�`�c�~�`�d���`�a�~�`�b�������E�E�E�@
����A���ׂ��̒藝���A�`�c�~�c�d���a�c�~�b�c�������E�E�E�A
�@�|�A���A
�`�c�i�`�d�|�c�d�j�������|����
�`�c2�������|����

NO.191�@�@�@�@ 11/7 �@�@���̗���@�@�@�F������̏h��
���A�n���̏�ɂ���F����s�m�@�����H���A
���{�̐l�����Ɍ������āA�h����o����܂����B
�Z�̂̉��̋�ł��B
�u���Ԃ�@���x���ł���@���d�́v
�ڂ����́A�F���J�����ƒc�̂g�o���������������B

NO.192 �@�@�@ 11/7 �@�@naomi �@�@�@ ���߂łƂ� �ꖜ�l�˔j���߂łƂ��������܂��B

NO.193 �@�@�@ 11/7 �@�@Junko �@�@�@ �W���|�X�̖��i�S�j ��ʂɂ��A���̐������Ƃ����݂��ɑf�i�ő�����P�j�ł���Ƃ��A �������A���炩�ɂ��Ƃ����݂��ɑf�łȂ��Ƃ��͂��߂ł��B
���鐔�ȏ�̐������ɂ���
���������{�����i�������A�����O�C�����O�Ȃ鐮���j
�Ə����\�����Ƃ��ł������ł��ˁB
���������f�A���������f�i�����P�j�Ƃ���ƁA
���������{����
�@����(�����f)�{��(�����f)
�@����(�����f�{�����f)
�ƂȂ�A���̔{�����������\���Ȃ����ƂɂȂ邩��ł��B

 E-mail
E-mail
 �߂�
�߂�