NO.1840丂丂丂妋棪偼柺愊斾[3](4) 丂2010.2.20.丂丂DDT
NO.1817丆NO.1826偲丄偙偺庤偺栤戣偵傕姷傟偰偒偨偺偱丄崱夞傕挧愴偟傑偡丅2偮偺栤戣偱妛傫偩偺偼丄師偺傛偆側庤弴偱偡丅
応崌暘偗偑柍尷屄偁傞暘晍妋棪傪埖偆応崌丄
丂丂(1)傑偡妋棪嬻娫傪愝掕偟丄妋棪1偵側傞傋偒慡懱愊倁傪寛傔傞丏
丂丂(2)丂(1)偵婎偯偄偰丄婯奿壔掕悢傪寛傔傞丏
丂丂(3)媮傔偨偄妋棪偺忦審偐傜丄倁偺拞偺椞堟俼傪掕傔傞丏
丂丂(4)俼偺懱愊傪媮傔丄倁偲偺斾傪庢傞丏
丂丂(5)斾偵婯奿壔掕悢傪妡偗傟偽丄媮傔偨偄妋棪丏
偲偄偆庤弴偱偡丅扤傕尵偭偰偔傟側偄偲巚偆偺偱姼偊偰尵偄傑偡偑丄悢妛偺妝偟偝偲偼丄摴嬶憿傝乮庤朄憿傝乯偺妝偟偝偩偲帺暘偼巚偭偰偄傑偡丅傑偀丄姰慡偵岺妛宯偺姶妎側偺偱偡偑丄NO.1817丆NO.1826偲偱偼丄偙偺庤偺妝偟偝傪枴傢偊偨偲巚偆偺偱丄崱夞傕摨偠曽恓偱峴偒傑偡乮嵞傃僸儞僩柍帇両乯丅
侾丏妋棪嬻娫偺愝掕
丂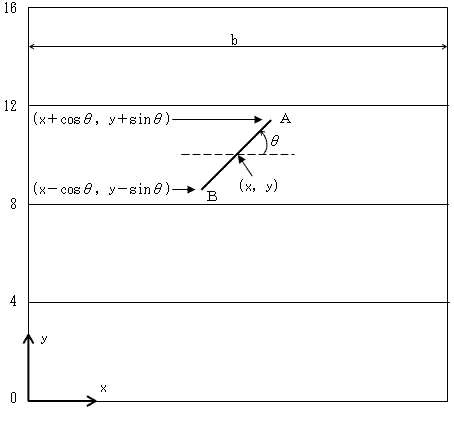
丂栤戣偵偼乽彴堦柺偵摍娫妘側暯峴慄孮偑傂偐傟偰丒丒丒乿偲偁偭偝傝彂偐傟偰偄傑偡偑丄彴偺戝偒偝偑桳尷偺応崌偲丄柍尷偵峀偄応崌偲偱丄偠偮偼栤戣偵側傝偦偆偱偡丅嵟弶偼丄桳尷偺応崌偐傜丅
丂彴偺墶亊廲傪b亊a偲偡傞丅偨偩偟a亖4倣偱丄倣偼0埲忋偺惍悢乮暯峴慄偺娫妘4乯丅
偦偆偡傞偲忋恾偺傛偆偵側傞丅偙偺偲偒恓偺椉抂揰偼懳徧偵埖偄偨偄偺偱丄恓偺拞揰傪(x丆y)偲偟偰丄
丂丂俙丗(x亄cos兤丆y亄sin兤)
丂丂俛丗(x亅cos兤丆y亅sin兤)
偱昞傢偣傞乮恓偺挿偝2乯丅兤偺斖埻偼丄0亝兤亙2兾丅
丂彴偺柺愊傪尷掕偟偰偟傑偭偨偺偱丄乽彴偵恓偑棊偪傞乿偲偄偆帠傕掕媊偟側偗傟偽側傜側偄丅
壗屘側傜棊偪偨恓偑丄彴傪偼傒弌偡応崌傕偁傝摼傞偐傜乮仼偙偺曈傝偼丄傑偝偵岺妛晹乯丅師偺傛偆偵掕媊偡傞丅
丂丂恓偺拞揰(x丆y)偑丄(x丆y) 伕[0丆b]亊[0丆a]偵棊偪偨帪丄恓偼彴偵棊偪偨偲掕媊偵偡傞丏
丂丂偙偙偱[0丆b]傗[0丆a]偼丄暵嬫娫丅
丂丒丒丒壗偐僸儞僩偵嬤偔側偭偰棃偨偧丒丒丒丅
傛偭偰妋棪嬻娫偼丄[0丆b]亊[0丆a]亊[0丆2兾]偲側傞丅x丆y丆兤曽岦偺婯奿壔掕悢偼丄
1/b亊dx丆1/a亊dy丆1/2兾亊d兤丅
俀丏岎傢傞忦審
丂恓偺挿偝偼暯峴慄偺娫妘傛傝抁偄偐傜丄恓傪偳偆搳偘偰傕丄暯峴慄偺1杮偲偟偐岎傢傟側偄丅
偪側傒偵偙偺曈傕岺妛晹偺姶妎偱偡丅
乮恓偑2杮埲忋偺暯峴慄偲岎傢傞側傜丄乽応崌傢偗傪傗偭偰偆傗傠偆偠傖側偄偐両乿偲偄偆婥偵側偭偰偟傑偆乯
丂廬偭偰丄恓偲暯峴慄偑岎傢傞忦審偼丄([恓偺俙揰偺y嵗昗]亅4値)偲([恓偺俛揰偺y嵗昗]亅4値)偑丄堎晞崋偺応崌偱偡丅
偙偙偱丄0亝値亝倣偱丄値偼惍悢丅偦傟偼丄
丂丂(y亄sin兤亅4値)( y亅sin兤亅4値) 亝0丂丂(1)
偲彂偗傑偡丅
丂傑偢x偑徚偊偨偐傜丄彴偺暆偼柍尷偵峀偔偰傕椙偄丅偦偟偰偙偺忦審偼丄(y丆兤)偱峫偊傟偽椙偄偺偱丄2師尦乮柺愊斾乯偵側偭偨両丅(1)傪揥奐偡傞偲丄
丂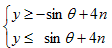
傑偨偼丄
丂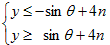
偲偄偆帠偩偐傜丄値亖1偺応崌偱僌儔僼偵偟偰傒傞偲丄壓恾偺傛偆偵側傞丅
丂僴僢僠晹偑媮傔傞柺愊丅僴僢僠晹偺柺愊偼丄
丂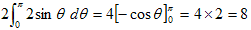
丂廬偭偰丄0亝y亝4倣偺帪偼丄1亝値亝倣亅1偵偮偄偰撈棫帋峴側傞偺偱丄8亊(倣亅1)偑媮傔傞柺愊丅
丂値亖0偲倣偵偮偄偰偼丄壓婰僴僢僠晹偺忋敿暘偲壓敿暘偑偦傟偧傟桳岠偵側傞偐傜丄寢嬊丄傕偆堦偮8傪懌偟偰8倣丅
丂傛偭偰媮傔傞妋棪偼丄婯奿壔掕悢傪峫椂偟偰乮a亖4倣乯丄
丂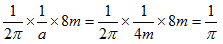
偲寁嶼偱偒傞丅偙偺寢壥偵傕廲暆偼娷傑傟偰偄側偄偐傜丄妋棪偼廲暆偵傕塭嬁偝傟偢丄
柍尷偵彴偑峀偔偰傕摨偠寢壥偵側傞丅偨偩偟廲暆偑偒偭偪傝4偺攞悢偱側偄帪偼丄傕偆彮偟暋嶨偵側偭偰丄
攞悢偱妱傝愗傟側偄抂悢偑晅偔偩傠偆偑丄偦傟偼a仺亣偺嬌尷堏峴偱0偵側傞偲梊憐偱偒傞偟丄偙傟偑媮傔傜傟偰偄傞寢壥巚偊傞丅
摎偊丗
丂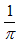
丂崱夞偼乽惓夝傪嫵偊偰壓偝偄丒丒丒乿側偳偲媰偒尵偼尵偄傑偣傫丅
僐儘僉僂儉幒偺僨乕儅暿偺晹壆偵丄價儏僢僼僅儞偺恓栤戣偑偁傞傕傫偹両丅丒丒丒偆傫丄惓偟偄傛偆偩丒丒丒^^丅傔偱偨偟丄傔偱偨偟丒丒丒^^丅
丂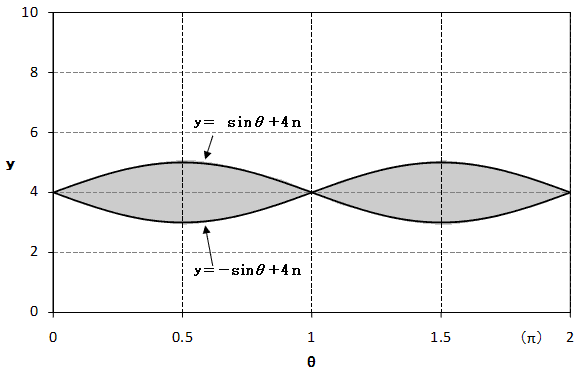
NO.1839丂丂丂栤戣157偺暍柺嶼(3) 丂2010.2.20.丂丂栭傆偐偟偺偮傜偄偍偠偝傫
仸 乽倢乮彫暥帤偺僄儖乯乿偼悢帤偺乽侾乿偲嬫暿偑偮偒偵偔偄偺偱丄乽値乿偱昞偡偙偲偵偟傑偡丅
仠丂偙偺寁嶼傪忋俀寘偲壓俀寘偵暘偗偰峫偊傑偡丅
丂丂忋俀寘偺寁嶼偺堦偺埵偼丄壓俀寘偺曽偐傜偺孞傝忋偑傝偑偁傞偐側偄偐傢偐傜側偄偺偱摎偊傪倣乫偲偟傑偡丅
丂丂壓俀寘偺寁嶼偺昐偺埵偼廫偺埵偐傜偺孞傝忋偑傝偑偁傞偐側偄偐傢偐傜側偄偺偱摎偊傪倣乫乫偲偟傑偡丅
丂丂乮倣乫乫偼侽偐侾偱偡乯
丂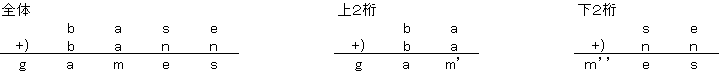
孞傝忋偑傝偺偙偲傪峫偊傞偲丄倗亖侾偱偡丅
仠丂壓俀寘偵偮偄偰
丂丂倱倕亄値値亖倣乫乫倕倱
丂丂乮侾侽倱亄倕乯亄侾侾亊値亖侾侽侽倣乫乫亄侾侽倕亄倱
丂丂俋倱亅俋倕亄侾侾値亖侾侽侽倣乫乫
丂丂俋乮倱亅倕乯亄侾侾値亖侾侽侽倣乫乫
丂丒丂丂倣乫乫亖侽偺偲偒
丂丂丂俋乮倕亅倱乯亖侾侾値
丂丂丂塃曈偼侾侾偺攞悢偵側傝傑偡丅
丂丂丂乮倕亅倱乯偺場悢偵侾侾偼側偄偺偱丄倕亖倱丆値亖侽偟偐壜擻惈偑偁傝傑偣傫丅
丂丂丂傛偭偰丄偙偺応崌偼晄揔摉偱偡丅
丂丂丂乮倕偲倱偼堎側傞偲偟偰乯
丂丒丂丂倣乫乫亖侾偺偲偒
丂丂丂俋乮倱亅倕乯亄侾侾値亖侾侽侽
丂丂丂偙偺幃傪枮偨偡偺偼丄値亖俆丄倱亅倕亖俆偺偲偒偟偐偁傝傑偣傫丅
丂丂
| 侾侾値 | 0 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99
|
|---|
| 俋乮倱亅倕乯 | 100 | 89 | 78 | 67 | 56 | 45 | 34 | 23 | 12 | 1
|
|---|
| 敾抐 | 亊 | 亊 | 亊 | 亊 | 亊 | 仜 | 亊 | 亊 | 亊 | 亊
|
|---|
偙偺昞偺俀峴栚偺悢偑俋偺攞悢偵側偭偰偄傞偺偼値亖俆偺偲偒偩偗偱偡丅
丂丂丂倱亅倕亖俆偲側傞偺偱丄倱偲倕偺壜擻惈偼師偺傛偆偵側傝傑偡丅
丂丂丂乮倱丆倕乯亖乮俈丆俀乯丄乮俉丆俁乯丄乮俋丆係乯
丂丂丂乮倗亖侾丄値亖俆傛傝丄侾偲俆偺側偄傕偺乯
仠丂忋俀寘偵偮偄偰
丂丂倐倎亄倐倎亖侾倎倣乫
丂丂俀亊乮侾侽倐亄倎乯亖侾侽侽亄侾侽倎亄倣乫
丂丂侾侽亊乮俀倐亅倎乯亄乮俀倎亅倣乫乯亖侾侽侽
丂丂偙偺幃偺嵍曈偺慜敿偼侾侽偺攞悢偱偡丅
丂丒丂丂嵍曈偺屻敿偺乮俀倎亅倣乫乯偑侽偺偲偒丄
丂丂丂乮俀倐亅倎乯偼侾侽偱偡丅
丂丂丂偩偐傜丄壜擻惈偼乮倐丆倎乯亖乮俇丆俀乯丄乮俈丆係乯偱偡丅
丂丂丂乮倗亖侾丄値亖俆傛傝丄侾偲俆偺側偄傕偺丅傑偨乮俉丆俇乯丄乮俋丆俉乯偼丄侾偺埵偺孞傝忋偑傝偑偁傞偺偱彍偒傑偡乯
丂
丂丒丂丂嵍曈偺屻敿偺乮俀倎亅倣乫乯偑侾侽偺偲偒丄乮俀倐亅倎乯偼俋偱偡丅
丂丂丂偩偐傜丄壜擻惈偼乮倐丆倎乯亖乮俉丆俈乯偱偡丅
丂丂丂乮倗亖侾丄値亖俆傛傝丄侾偲俆偺側偄傕偺丅傑偨乮俇丆俁乯偼孞傝忋偑傜側偄偺偱彍偔丅乮俋丆俋乯偼摨偠悢側偺偱彍偔乯
丂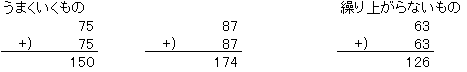
仠 埲忋偐傜丄乮倐丆倎乯偺壜擻惈偼丄乮俇丆俀乯丄乮俈丆係乯丄乮俉丆俈乯
丂丂丂乮倱丆倕乯偺壜擻惈偼丄乮俈丆俀乯丄乮俉丆俁乯乮俋丆係乯
丂丂丂傛偭偰丄乮倐倎倱倕乯偺壜擻惈偼丄摨偠悢帤偑廳側傜側偄傛偆偵乮俇俀俉俁乯丄乮俇俀俋係乯丄乮俈係俉俁乯丄乮俉俈俋係乯偱偡丅偙傟傜傪帋偟偰傒傞偲丄
丂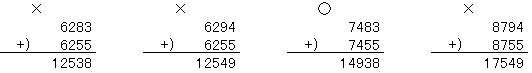
侾丄俀丄係斣栚偼摎偊偺昐偺埵偑俆偲側傝偆傑偔偁傝傑偣傫丅
傛偭偰丄倐倎倱倕亄倐倎倢倢亖倗倎倣倕倱偼
俈係俉俁亄俈係俆俆亖侾係俋俁俉偱偡丅
NO.1838丂丂丂丂丂桳柤側柍尷媺悢丂丂2010.1.15.丂丂悈偺棳傟
戞俀俁俈夞悢妛揑側墳曞栤戣
庴尡惗偱偁傞惗搆偐傜丄2010擭摨巙幮戝妛偺擖帋栤戣傪尒傞偙偲偑偱偒傑偟偨丅
1996擭嶥杫堛壢戝偵弌偨栤戣偲傛偔帡偰偄傑偡偐傜丄斾妑偟側偑傜夝偄偰傒偰偔偩偝偄丅
傑偢偼丄嶥杫堛壢戝偺擖帋栤戣偱偡丅

師偵摨幮戝妛偺栤戣偱偡丅

拲丗偙偺婰帠偵娭偡傞搳峞偺宖嵹偼丄2010擭3寧8擔埲崀偲偟傑偡丅
NO.1837丂丂丂妋棪偼柺愊斾[3](3) 丂2010.2.15.丂丂junko
乽價儏僢僼僅儞偺恓偺幚尡乿偲屇偽傟傞僔儈儏儗乕僔儑儞偵傛偭偰墌廃棪兾
傪嬤帡偡傞偲偄偆傕偺偱偡偹丅
偐偮偰丄僔儈儏儗乕僔儑儞僾儘僌儔儉傪嶌偭偨傕偺偑偁傝傑偡偺偱丄偍帋偟偔偩偝偄丅
丂丂價儏僢僼僅儞偺恓偺幚尡偵傛傞墌廃棪兾
暯峴慄偺娫妘30偵懳偟偰恓偺挿偝偲搳偘傞杮悢傪巜掕偟偰丄暯峴慄偲岎傢傞恓偺杮悢傪悢偊丄
偦偙偐傜墌廃棪兾傪嬤帡偡傞偲偄偆傕偺偱偡丅
NO.1836丂丂丂妋棪偼柺愊斾[3](2) 丂2010.2.15.丂丂栭傆偐偟偺偮傜偄偍偠偝傫
恓偑偳偙偵棊偪傞偐暘偐傜側偄偙偲偲丄摨偠忬懺偑孞傝曉偝傟傞偙偲偐傜
侾杮偺慄偺嵍塃俀cm乮寁係cm乯偺暆偺拞偱峫偊傑偡丅
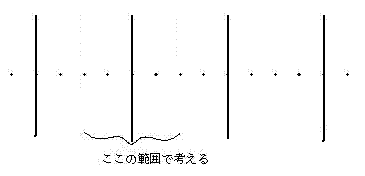
恓偺拞怱偼偳偙偵偱傕摨偠傛偆偵棊偪傞偲峫偊傜傟傞偺偱丄偦偺妋棪暘晍傪 倫乮倶乯亖侾乛係 偲峫偊傑偡丅
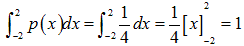
恓偺拞怱偑丄慄偐傜侾cm埲忋棧傟傞偲慄偲岎傢傞偙偲偼偁傝傑偣傫丅
恾偺愒偺晹暘偵拞怱偑偁傞偲岎傢傝傑偣傫丅
恾偺惵偺晹暘偵拞怱偑偁傞偲岎傢傞壜擻惈偑偁傝傑偡丅
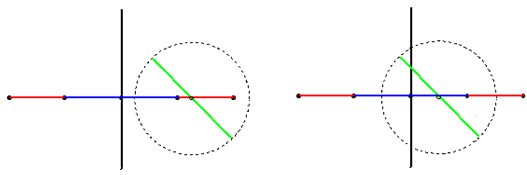
恓偺拞怱偑慄偲岎傢傞壜擻惈偑偁傞埵抲偺偲偒傪峫偊傑偡丅
恓偲慄偑偓傝偓傝偱嫟桳揰傪帩偮応崌偺妏傪塃廃傝偵偼偐偭偰兤偲偟傑偡丅
恓偺拞怱偑偦偺埵抲偵偁傞偲偒慄偲岎傢傞妋棪偼 倯亖4兤乛2兾 偱偡丅
慄偐傜恓偺拞怱傑偱偺嫍棧傪倶偲偡傞偲丄恓偺挿偝偑俀cm側偺偱丄cos兤亖倶偱偡丅
兤傪倶偱昞偡偲丄兤亖cos-1倶 偱偡丅
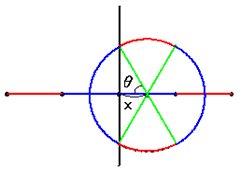
埲忋偐傜慄偺塃敿暘傪峫偊偰俀攞偟偰妋棪傪媮傔傑偡丅
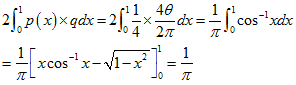
屘偵丄侾乛兾偲側傝傑偡丅
NO.1835丂丂丂栤戣157偺暍柺嶼(2) 丂2010.2.11.丂丂昹揷丂柧枻
7483
7455
-------
14938
Option Explicit
' BASE
'+ BALL
'------
' GAMES, 暥帤偼屳偄偵堎側傞. B,G亗0
Sub Macro1()
Sheets("Sheet1").Select
Dim B As Integer
Dim A As Integer
Dim S As Integer
Dim E As Integer
Dim L As Integer
Dim G As Integer
Dim M As Integer
Dim kuriagari(3) As Integer
Dim gyou As Integer
Cells(1, 1).Value = 0
Range("A1").Select
For E = 0 To 9
For L = 0 To 9
If E <> L Then
S = (E + L) Mod 10
If E <> S And L <> S Then
kuriagari(1) = (E + L) \ 10
If (S + L + kuriagari(1)) Mod 10 = E Then
kuriagari(2) = (S + L + kuriagari(1)) \ 10
For A = 0 To 9
If E <> A And L <> A And S <> A Then
M = (A + A + kuriagari(2)) Mod 10
If E <> M And L <> M And S <> M And A <> M Then
kuriagari(3) = (A + A + kuriagari(2)) \ 10
For B = 1 To 9
If E <> B And L <> B And S <> B And A <> B And M <> B Then
If (B + B + kuriagari(3)) Mod 10 = A Then
G = (B + B + kuriagari(3)) \ 10
If G > 0 And E <> G And L <> G And S <> G And A <> G And M <> G And B <> G Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
gyou = Cells(1, 1).Value * 4 - 3
Cells(gyou, 3).Value = B * 1000 + A * 100 + S * 10 + E
Cells(gyou + 1, 2).Value = "+"
Cells(gyou + 1, 3).Value = B * 1000 + A * 100 + L * 10 + L
Cells(gyou + 2, 3).Value = G * 10000 + A * 1000 + M * 100 + E * 10 + S
Call keisen(gyou + 1)
End If
End If
End If
Next B
End If
End If
Next A
End If
End If
End If
Next L
Next E
End Sub
Sub keisen(ByVal gyou As Integer)
Range("B" + strr(gyou) + ":C" + strr(gyou)).Select
Selection.Borders(xlDiagonalDown).LineStyle = xlNone
Selection.Borders(xlDiagonalUp).LineStyle = xlNone
Selection.Borders(xlEdgeLeft).LineStyle = xlNone
Selection.Borders(xlEdgeTop).LineStyle = xlNone
With Selection.Borders(xlEdgeBottom)
.LineStyle = xlContinuous
.Weight = xlThin
.ColorIndex = xlAutomatic
End With
Selection.Borders(xlEdgeRight).LineStyle = xlNone
Selection.Borders(xlInsideVertical).LineStyle = xlNone
Range("A1").Select
End Sub
Private Function strr(ByVal n As Integer) As String
strr = Right(Str(n), Len(Str(n)) - 1)
End Function
NO.1834丂丂丂栤戣157偺暍柺嶼丂丂丂 丂2010.2.11.丂丂柪巕偺梇擫
丂丂丂丂俛俙俽俤丂丂丂丂丂俈係俉俁丂
丂亄丂丂俛俙俴俴丂丂亄丂丂俈係俆俆
丂亅亅亅亅亅亅亅亅丂亅亅亅亅亅亅亅亅
丂丂丂俧俙俵俤俽丂丂丂丂侾係俋俁俉
俧亖侾丄俛亖俆乣俋傑偱偼娙扨丅
俴亖俆偵婥偯偄偨偲偒偼婐偟偐偭偨偱偡丅
NO.1833丂丂丂僲儖儉 丂 2010.2.7.丂丂俼倄倀1128
妛惗帪戙儀僋僩儖偲峴楍偺庼嬈傪寚惾偟偨偨傔崱偲偰傕嬯楯偟偰偄傑偡丅乮嵟嬤偵
側偭偰嵟彫擇忔朄傪巊偆昁梫偵敆傜傟恾彂娰偱嶲峫彂傪庁傝偰偒偨偲偙傠丄峴楍儀僋
僩儖偺棐偱偡乯
偦偙偱僂儘僂儘偟側偑傜怓乆側撉傒嫏傝傪偟偰偄偨傜僲儖儉偲偄偆尵梩偑弌偰偒傑偟
偨丅側偵傗傜嫍棧傪昞偡尵梩偺傛偆偱偡偑丄僷僜僐儞偱MAX偲偄偆娭悢傪巊偆偲嵟戝
抣偑娙扨偵慖傃弌偣傑偡偑丄壓婰偺P傪柍尷戝偵偟偨偲偒嵟戝抣偑弌傑偡丅柍尷戝僲儖儉偲尵偆偦偆偱偡丅
栚偐傜偆傠偙偱偟偨丅場傒偵P=2偺応崌暥帤捠傝嫍棧偱儐乕僋儕僢僪僲儖儉乮捈姶偵
偲偰傕嬤偄乯偲尵偆偦偆偱偡丅
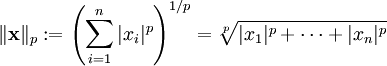
偦偙偱嵟戝抣偑嬌尷偱昞偣傞側傜丄嵟彫抣乮俵俬俶乯傗丄拞墰抣乮median乯偼偳偆偱
偟傚偆偐丅
NO.1832丂丂丂妏搙傪媮傔傞栤戣(3) 丂2010.2.1.丂丂栭傆偐偟偺偮傜偄偍偠偝傫
僄儗僈儞僩偱側偄夝摎傪堦偮丅
 恾偺傛偆偵A偐傜BD偵悅慄AH傪偍傠偟傑偡丅
恾偺傛偆偵A偐傜BD偵悅慄AH傪偍傠偟傑偡丅
AC偲BD偺岎揰E偐傜BC偵悅慄EF傪偍傠偟傑偡丅
仮ABD偼擇摍曈嶰妏宍偱偡丅
仮ABH偲仮CEF偼憡帡偱偡丅
曈AB偺挿偝傪侾偲偟傑偡丅
佢DCE亖倶丄佢CDE亖倷偲偟傑偡丅
AH亖sin 50亱丄AD亖侾丄BH亖DH亖sin 40亱
仮AHD偵偍偄偰丄AE偑妏偺擇摍暘慄側偺偱丄AH丗AD亖HE丗ED傛傝
HE亖HD亊AH乛乮AD亄AH)亖sin 40亱sin 50亱乛乮侾亄sin 50亱乯
ED亖HD亊AD乛乮AD亄AH)亖sin 40亱乛乮侾亄sin 50亱乯
BE亖BH亄HE亖sin 40亱亄sin 40亱sin 50亱乛乮侾亄sin 50亱乯
丂丂亖sin 40亱乮侾亄俀sin 50亱乯乛乮侾亄sin 50亱乯
EF亖侾乛俀亊BE亖sin 40亱乮侾亄俀sin 50亱乯乛俀乮侾亄sin 50亱乯
仮CEF偵偍偄偰丄CE sin 40亱亖EF傛傝
CE亖乮侾亄俀sin 50亱乯乛俀乮侾亄sin 50亱乯
仮BCE偺柺愊傪峫偊傞偲丄BC亊EF亖BE亊CE sin 70亱傛傝
BC亖BE亊CE sin 70亱乛EF亖sin 70亱乮侾亄俀sin 50亱乯乛乮侾亄sin 50亱乯
仮CDE偱惓尫掕棟傪峫偊傞偲丄
ED乛sin 倶亖CE乛sin 倷丂丒丒丒丂嘆
仮BCD偱惓尫掕棟傪峫偊傞偲丄
BC乛sin 倷亖BD乛sin乮倶亄40亱乯丂丒丒丒丂嘇
嘆丄嘇傪偐偗崌傢偣偰暘曣傪暐偆偲丄
ED亊BC sin乮倶亄40亱乯亖CE亊BD sin 倶傛傝
sin 40亱乛乮侾亄sin 50亱乯亊sin 70亱乮侾亄俀sin 50亱乯乛乮侾亄sin 50亱乯亊乮sin 倶 cos 40亱亄cos 倶 sin 40亱乯
丂丂丂亖乮侾亄俀sin 50亱乯乛俀乮侾亄sin 50亱乯亊俀sin 40亱亊sin 倶
sin 70亱乛乮侾亄sin50亱乯亊乮sin 倶 cos 40亱亄cos 倶 sin 40亱乯亖sin 倶
sin 70亱cos 40亱sin 倶亄sin 70亱sin 40亱cos倶亖乮侾亄sin 50亱乯sin 倶
乮sin 70亱 cos40亱亅侾亅sin 50亱乯sin 倶亖亅sin 70亱sin 40亱cos 倶
tan 倶亖亅sin 70亱sin 40亱乛乮sin 70亱cos 40亱亅侾亅sin 50亱乯
丂丂丂亖亅sin 70亱sin 40亱乛乮sin 70亱cos 40亱亅侾亅cos 40亱乯
丂丂丂亖亅cos 20亱sin 40亱乛乮cos 20亱cos 40亱亅俀cos2 20亱乯
丂丂丂亖亅sin 40亱乛乮cos 40亱亅俀cos 20亱乯
丂丂丂亖sin 40亱乛乮cos 20亱亅cos 40亱亄cos 20亱乯
丂丂丂亖sin 40亱乛乮cos 20亱亅cos 40亱亄cos 20亱乯
丂丂丂亖sin 40亱乛乮俀sin 30亱sin 10亱亄sin 70亱乯
丂丂丂亖sin 40亱乛乮sin 10亱亄sin 70亱乯
丂丂丂亖sin 40亱乛乮俀sin 40亱cos 30亱乯
丂丂丂亖侾乛併俁
亪倃亖俁侽亱
傛偭偰佢俛俠俢亖俈侽亱
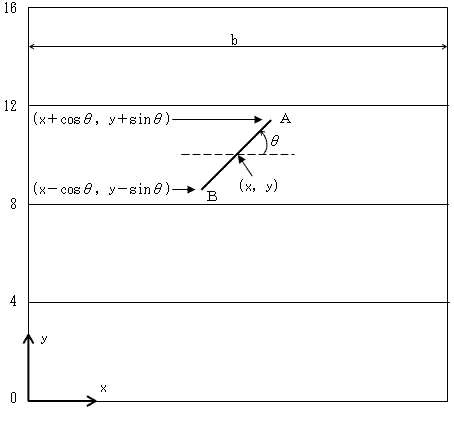
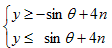
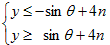
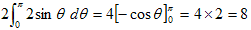
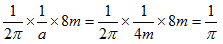
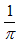
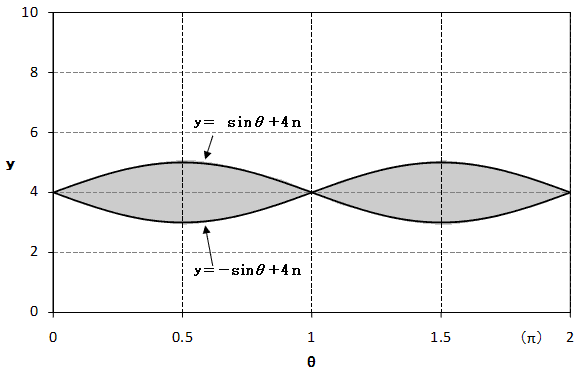
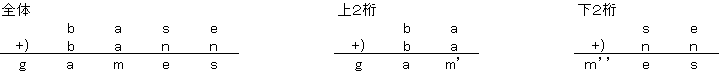

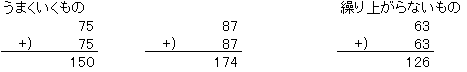
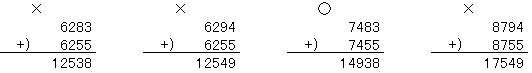



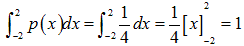


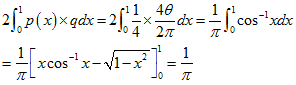
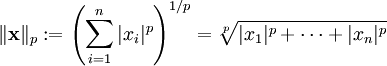
 恾偺傛偆偵A偐傜BD偵悅慄AH傪偍傠偟傑偡丅
恾偺傛偆偵A偐傜BD偵悅慄AH傪偍傠偟傑偡丅