NO.1819 ハイポサイクロイド(3) 2009.12.26. kohji
(1)
円Dの中心をQとおき; 複素数でQの位置をq、 P の位置をp で表す。
円Cと円Dとが接する部分の長さは等しいので、
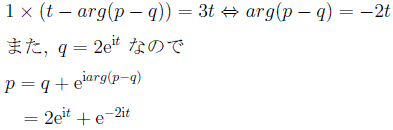
(2)
この曲線の長さL は、
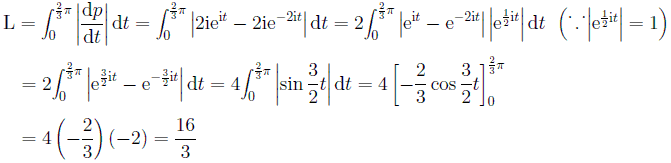
ColloquiumNO.250
|
(1)
円Dの中心をQとおき; 複素数でQの位置をq、 P の位置をp で表す。
円Cと円Dとが接する部分の長さは等しいので、
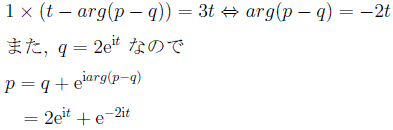
(2)
この曲線の長さL は、
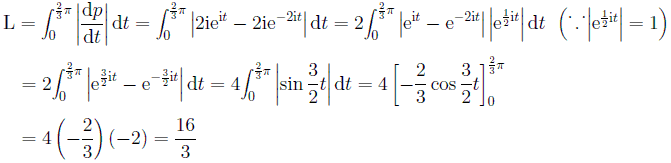
問題1.
平面(ユークリッド平面)は、1本の直線によって2個の領域に、2本の直
線によって最大4個の領域に、3本の直線によって最大7個の領域に、それぞれ分割
されます。n本の直線によって最大何個の領域に分割されるか、nを用いて式で表し
てください。
問題2.
球面は、1個の円(大円)によって2個の領域に、2個の円によって最大4
個の領域に、3個の円によって最大8個の領域に、それぞれ分割されます。n個の円
によって最大何個の領域に分割されるか、nを用いて式で表してください。
問題3.
空間(三次元空間)は、1枚の平面によって2個の領域に、2枚の平面に
よって最大4個の領域に、3枚の平面によって最大8個の領域に、それぞれ分割され
ます。n枚の平面によって最大何個の領域に分割されるか、nを用いて式で表してく
ださい。
皆さん、場合の数が無数にある確率の問題を考えたことがありますか。
ここで、問題です。
a,bを a<bである任意に与えられた正の数とする。
長さbの線分上に勝手に2点をとるとき,それら2点間の距離がa以上である確率を求めよ。
注:この記事に関する投稿の掲載は、2010年1月4日以降とします。
一部修正(12.18)
(1)
下の表のように自然数を横に6個ずつ並べていきます。
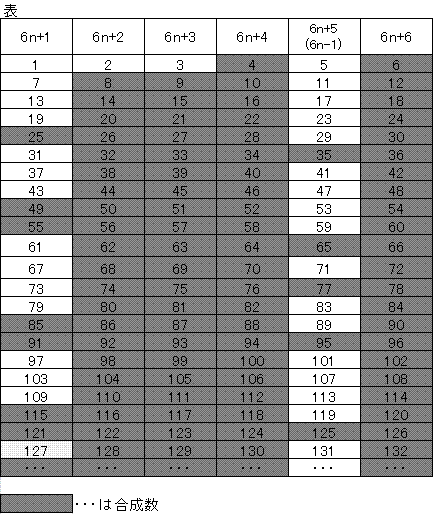
すると、
6n+2=2×(3n+1) ・・・ 2の倍数
6n+3=3×(2n+1) ・・・ 3の倍数
6n+4=2×(3n+2) ・・・ 2の倍数
6n+6=6×(n+1) ・・・ 6の倍数
のように、それぞれの倍数が縦に並びます。
だからその列の下に5以上の素数は現れません。
だから5以上の素数は、6n+1か6n-1の列にしか現れません。
(2)
6N-1が素数だとすれば、自分自身が6n-1の形の素数の倍数です。
6N-1が合成数だとすれば、pkを素数として分解ができます。
6N-1=p1×p2×・・・
さて、
6N-1=2×3×N-1
なので、2と3は素因数にありません。
だから、素因数は5以上なので、(1)より6n+1または6n-1の形です。
さて、6n+1の形の数は、
(6m+1)×(6n+1)=36mn+6m+6n+1=6×(6mn+m+n)+1
のようにいくつかけても6n+1の形にしかなりません。
だから、6n+1の形の素数だけで6n-1の形の数をつくることはできません。
また、6n-1の形の数は、
(6m-1)×(6n-1)=36mn-6m-6n+1=6×(6mn-m-n)+1
のように偶数個かけると6n+1の形になります。
以上から6N-1の形の合成数は、6n-1の形の素因数を奇数個もちます。
(3)
6n-1の形の素数が有限個だとします。
そのすべてのリストを、{q1,q2,・・・,qk}とします。
ここで次の形の数Aを考えます。
A=2×3×q1×q2×・・・×qk-1
(=6×N-1)
Aが素数だとすれば、Aはリストにない6n-1の形の素数です。
Aが合成数だとすれば、(2)より6n-1の形の素数を因数にもちます。
ところがこの数はやはりリストにありません。
以上から6n-1の形の素数は無限に多く存在します。
