
Weekend Mathematics/コロキウム室/テーマ別/38.ビュッフォンの針の実験
NO.441 '99 4/14 水の流れ ビュッフォンの針の実験
昔、ビュッフォン(Buffon)の針の実験をしたことがあります。
大きな紙に間隔がdの平行線をたくさん引き、
長さkの針をばらばらに落としたとき、
針が平行線と交わる確率pは
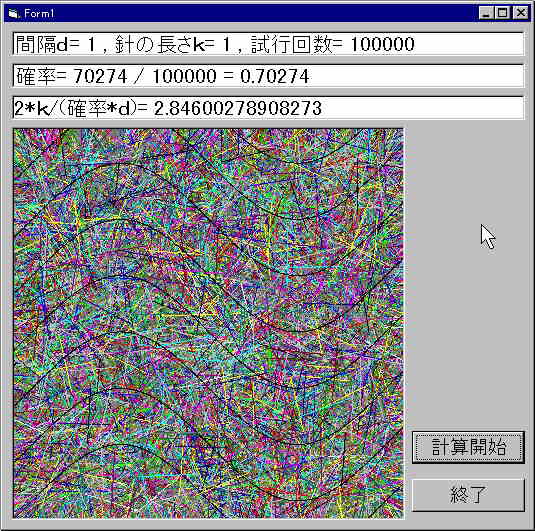
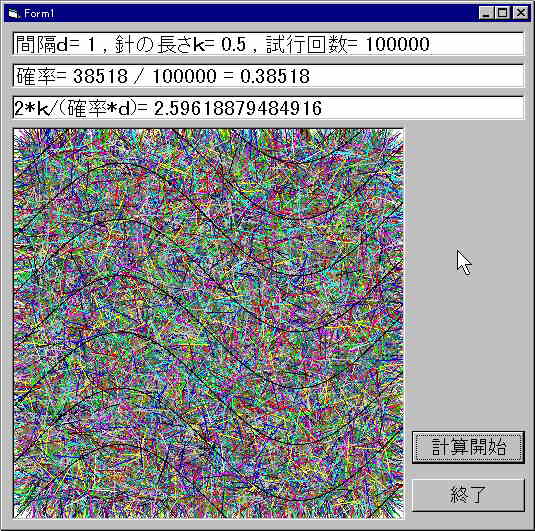
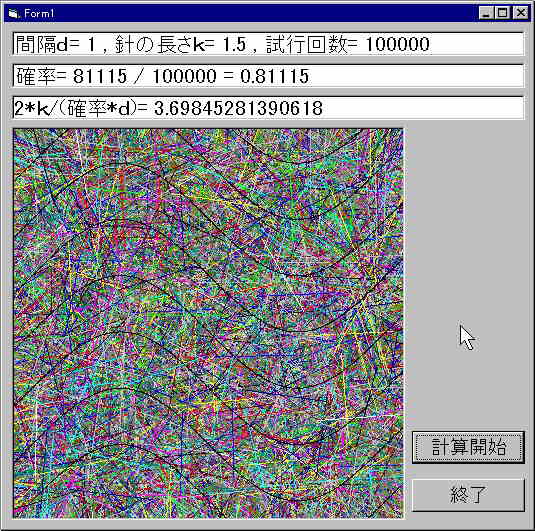
p=2k/πd
となることを証明してください。
実験では、多数の針を落として(もちろん、
針を使ってけがをしないように取り扱ってください)、
次の式からpを求めます。
p=(平行線にかかった針の数)÷(落とした針の数)
そこで、皆さん一度試してみてください。
準備するもの。
d=8cm 、k=4cm のとして、針を千本と大きなビー紙

NO.446 '99 4/21 水の流れ ビュッフォンの針の実験(2)
p=2k/πdとなることを証明しましょう。
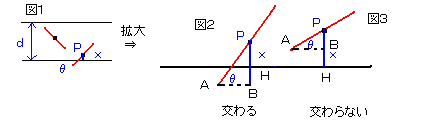 <考え方>
<考え方>
1本の針を任意に床に落としたときの図1を見てください。
針が平行線と交わるとしたら、針の中点Pから最も近い平行線の1本と交わる。
針の中点Pと平行線のうちの一番近い直線との距離をxとし、
針とその平行線のなす角をθとおく。(図2参照)
このとき、変数x、θの変域は、0≦θ<π、0≦x≦d/2…(*) である。
座標平面上に、変域(*)を図示し、また、針が直線と交わるθとxに関する条件を
求め、それを座標平面に図示し、両者の面積比を求める。
なお、針の端点が平行線上にある場合は「交わっている」ものとして扱っても
「交わっていない」として扱っても結果は同じである。
ここでは、「交わっている」ものとして扱うことにする。
 【解答】ただし、d≧kの場合を考えます。
【解答】ただし、d≧kの場合を考えます。
針が平行線の1つと交わる条件とは、針の中点から一番近い平行線と交わることである。
図2を見て下さい。
針が一番近い平行線と交わる方の端点をA、中点をP、点Pから一番近い平行線に垂線PHを引く。
また、Aを通り平行線を引き、垂線PHとの交点をBとおく。
さらに、∠PAB=θ とおく。
すると、PA=k/2,PB=(k/2)×sinθ
したがって、xとPBの関係より、交わる条件は x≦(k/2)×sinθ
交わらない条件は x>(k/2)×sinθ である。<図3を参照>
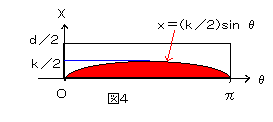
よって、交わる条件を座標平面で書くと、図4になります。
したがって、求める確率pは


| NO.473 | '99 5/15 | Junko | ビュッフォンの針の実験(3) |
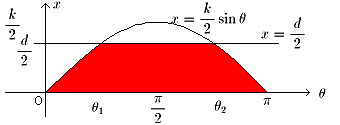
d<kの場合について考えました。
右の図の赤い部分の面積を求めればいいことになります。
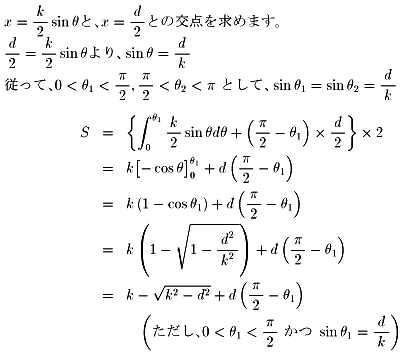

| NO.862 | 2000.10.1. | 月の光 | ビュッフォンの針の実験(4) |
NO.441のビュフォンの針の問題では間隔がdの平行線をたくさん引き、
長さkの針をばらばらに落としたとき、 針が平行線と交わる確率pを
求めますが、ではy=sinθ,y=sinθ+d,y=sinθ+2d,y=sinθ+3d・・・
と無限に線を引き、その上に長さkの針を落としたときに線と針が交わ
る確率はどうなるでしょうか。

| NO.869 | 2000.10.14. | 浜田 明巳 | ビュッフォンの針の実験(5) |
VBで実験したところ、以上のような結果になりました。精度が悪いせいか、いい結果とはいえないでしょう。

 戻る
戻る