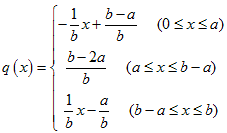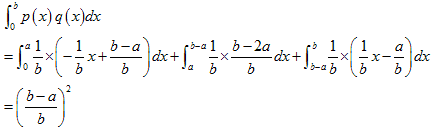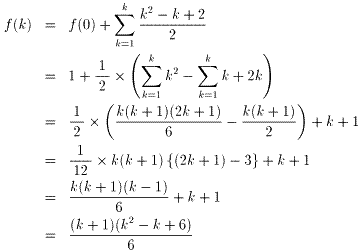NO.1828 角度を求める問題(2) 2010.1.24. RYU1128
AD及びBCを各々D,C方向に延長しその交点をEとする。
Cを通りABに平行な直線とAEの交点をFとする。
BFとACの交点をGとする。
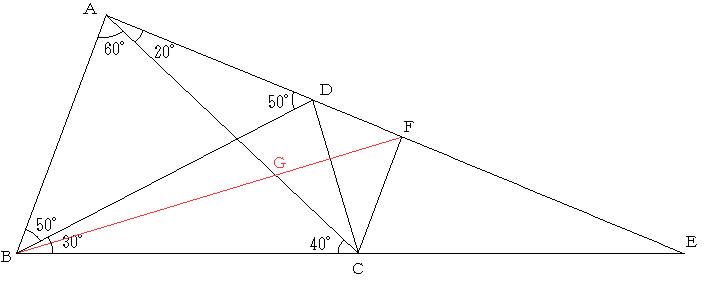
CFGは正三角形。
角GFDは40度
角ADB=角ABD=50度よりAB=AD、三角形ABGは正三角形なのでAB=AG故にAD=AG
よって角AGD=80度
CFGは正三角形なので、角DGFは40度
このことから、三角形DFGは底角40度の二等辺三角形。よってFGとCDは直交する。
CFGは正三角形だから角DCG=ACD=30度
角BCD=40+30=70度
この問題は三十数年前に数学セミナーの“エレガントな回答を求む”に出ていまし
た。
ただし条件として、初等的に解くこととあったと記憶しています。
私は、50度を55度と記憶違いして30年ほど解けませんでした。
ごく最近作図しなおして間違いに気づきやっと解けました。
当時も初等的なというところに引っかかって応募者が少なかったのを記憶していま
す。
NO.1827 角度を求める問題 2010.1.17. K.F.
過去の日記に、このような問題のメモがあるのを見つけました。
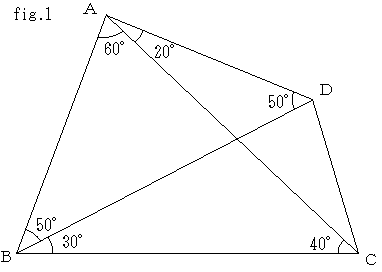
問題 ∠BCDの大きさを求めてください。
NO.1826 確率は面積比[2] 2010.1.4. 水の流れ
第235回数学的な応募問題
皆さん、場合の数が無数にある確率の問題を考えたことがありますか。ここで、問題です。
円周上に異なる3点A,B,Cを選び、三角形ABCを作る。このとき、
(1)直角三角形となる確率を求めよ。
(2)鋭角三角形となる確率を求めよ。
(3)鈍角三角形となる確率を求めよ。
ヒント:円の中心が三角形の周上または内部、外部にあるときを考えてください。
もちろん、他の解法を考えても構いません。
注:この記事に関する投稿の掲載は、2010年1月25日以降とします。
NO.1825 線形な(正直な?)エッセイ(?)其の1 2010.1.4. DDT
皆さん、擬ベクトルってご存知ですよね?。外積から生まれてくるベクトルの事です。
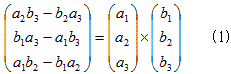
じつは工学部のほとんどの学生は、擬ベクトルの「擬」の意味もわからずに、外積を使っています。
というか、c=a×bのcは、ふつうのベクトル(極性ベクトル)と思っています。
実用上は、それでかまわないんですけど、たまに座標変換を行って、それが直交変換でない時に、いきなりぎょっとします。
変換行列をSとして、
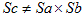
だからです。まぁ、直交でない座標変換ですらめったにやらないので、こんな事もめったに体験しないですが、
それだけに一度でも経験すると、「外積、恐ろしやぁ〜」という感覚に襲われます。
そこで初めて「擬」の文字が気になって来ます。しかし「擬」の文字を知ってるって事は、
それなりに擬ベクトルを教わったはずなんですよ。しかし何故か理解していない。
自分も最初は何の事やらさっぱりで、「擬」なんて無視してました。
その原因は、擬ベクトルは教わっても、擬ベクトル空間の説明を、ちゃんと受けていないからではないか?。
それには3重苦の理由がある、というのが、ここでのお題です。
最初に、いちおう正式な擬ベクトルの定義を行います。擬ベクトルとは、3次元における2階の反対称テンソルの省略記法です。
2階のテンソルとは行列の事です。それが反対称とは、反対称行列を意味します。特に3次元の場合、
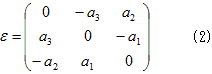
となり、反対称なεの独立成分は、上半分か下半分かの3個になります。
独立成分3個で3次元だから、εを3次元のベクトル、(a1,a2,a3)として略記すると便利だよなぁ〜、となって、擬ベクトルが導入されます。何故便利か?。
反対称行列は、無限小回転でのベクトルの移動を表す、というのがその理由です。
実際、回転行列(直交行列)をTとした時、Tが作用する位置ベクトルの移動は、Eを単位行列として、
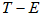
で表せます。回転が微小だとすると、T−E=εが微小なはずです。Eを移項してT=E+εとし、
Tが直交行列である事を使うと(tは、転置を表す)、
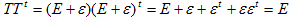
より、
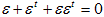
が得られます。ここでεが微小な事を使い、2次の微小量εεtを落とすと、
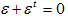
となって、εは反対称行列です。
εの独立成分の符号の取り方には任意性がありますが、例えばそれを(2)のように選ぶと、
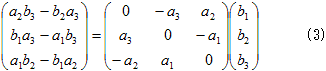
が得られ、(3)を(1)のように略記する、という訳です。
ε=(a1,a2,a3)=aは回転作用を表すので、これが回転の速度ベクトルです。
b=(b1,b2,b3)は、回転する質点の位置ベクトルに、
質量をかけたものと見なせるので、結局c=a×bが角運動量ベクトルという事になり、cはaにもbにも直交するので、回転軸の方向までわかります。確かに便利です。
そして(3)の形なら、cは普通のベクトルと、ちょっと違うかもしれないと、思いいたる事ができます。
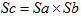
を想定していたが、本当は、
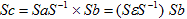
なので、成り立つかどうかわかりません。何故なら一般には、
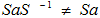
だからです。
(左辺は行列としての、右辺はベクトルとしてのaで、=は、右辺が左辺の省略記法として正しい、という意味です。
Sが直交変換の場合は正しい)
しかしこのような明解な説明に最初に出くわしたのは、数学関係の本ではありませんでした。
ゴールドスタインの古典力学で、剛体の運動学の部分を読んでいた時に知りました。
という事は、数学関係の本で、擬ベクトルの事をちゃんと説明しているものは、非常に少ないのではないか?、という事態になります。
いや現実は、もっと悪いです。数学(線形代数)では、擬ベクトルについて何か語る必要すらないからです。
何故なら、(3)によって擬ベクトルaを定義し、aを全て集めて集合V'(3次の反対称行列全体)を作ると、V'は線形空間の公理を全て満たして、
ベクトル空間になってしまいます。線形空間の公理は11個ありますが、擬ベクトルの単位元の存在とか明らかな事を除けば、
確認すべきは、次の2つです。
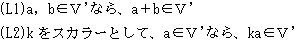
(L1)は、無限小回転の加法性から言えます。a,bが無限小回転なら、a+bも無限小回転を表す
(または、反対称行列の和は、反対称)。
(L2)も、aの実体が反対称行列という事から明らかです。
つまり線形代数の立場では、擬ベクトル空間も立派なベクトル空間です。
しかも擬ベクトル空間は3次元に特有なものなので、その次元は3で、もとのベクトル空間と見分けもつきません。同じ次元のベクトル空間は、全て同型だからです。
それは論点が違う!、という話はわかっています。擬(軸性)ベクトルは、極性(ふつうの)ベクトルと同じものか?、
で本質的に問われている事は、
極性ベクトル「空間」を土台にして作られた軸性ベクトル「空間」は、土台としたベクトル空間と、ベクトル空間として、はたして同じものか?.
だと思います。もう少し具体的に言うと、
極性ベクトル空間と軸性ベクトル空間は、同じ基底を持てるか?.
です。違いは、ベクトルとしての変換性の差として現れます(もともとはベクトルと行列なんだから、同じ基底なんか持てるわけない!)。次の一言は、自分も工学部の学生だったので、あえて言います。
「線形代数すらまともに理解しているとは思えない工学部の学生に、そんな話をして通じるのか?」です。そして数学科の学生は、擬ベクトルを意識する必要がありません。学生はどこに行っても、軸性ベクトル空間に関するちゃんとした説明を聞けない。これが現実だと思います。
最後にとどめを刺しましょう。ゴールドスタインの定式化が、数学的に正しいと自分は思いますが、この定式化は、次のようなものです。
[極性ベクトル]=[軸性ベクトル]×[極性ベクトル] (4)
ところが工学部の定式化は違います(方言だと思います)。
[軸性ベクトル]=[極性ベクトル]×[極性ベクトル] (5)
こうしないと(3)を、速度ベクトル×位置ベクトルのように見れないからですが、これは可能です。本当は、(4)の軸性ベクトルの変換性の違いから、
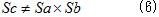
となりますが、(6)の結果を、左辺のcの変換性の違いだと見る事もできるからです。で、(5)で軸性ベクトルを定義しても、(4)は成り立ちます。逆も可能です。(5)を(4)に代入すると、
[極性ベクトル]=([極性ベクトル]×[極性ベクトル])×[極性ベクトル]
となりますが、これが有名な外積の3重積の公式、
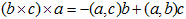
です。(,)は内積を表します。左辺でb,cは極性なので、b×cは軸性,aは極性。
それが右辺では、極性なb,cの張る平面内に戻って来るので、結局、軸性×極性の結果は、極性です。
これなどは、同じ表現((3))を二通りの意味に解釈すると、思わぬ結果が得られるという、
とっても数学らしい話だと思いますが、同じ表現を二通りの意味に解釈する時点で、学生はもう不安とパニックです。
(5)の方向で数学的に軸性を定義しようとすると、本一冊分の説明が必要になると気づかせてくれたのは、
やはり線形代数の大御所、伊理正夫先生でした。
シリーズ新しい応用の数学 1−1
ベクトル解析(ベクトルとテンソル第一部),伊理正夫/韓大舜,教育出版,1973年11月.
この本は多様体を意識して書かれているので、軸性,極性は内性,外性という言葉で区別され、擬ベクトル空間を一人前のベクトル空間として扱った、稀有な本です。なので見た目以上に、この本は難しいと思います。
以上の3重苦から、擬ベクトルってなかなかわからないよなぁ〜、って思います。
NO.1824 確率は面積比[1](4) 2010.1.4. kohji
線分上から任意の2 点を選び出したとする。このとき片方の端点と
この2 点からの距離をそれぞれx, y とすると、x, y は次の条件を満たす。
0≦x≦b, 0≦y≦b �・・・(*)
この2 点間の距離がa 以上の時x, y は次の条件を満たす。
|x − y|≧ a ・・・(**)
従って求める確率は、
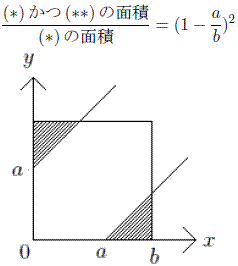
NO.1823 確率は面積比[1](3) 2010.1.4. DDT
1.ざっくり解答の試み
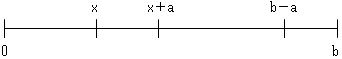 右図のように、座標を取って考えます。またここでは、Rを実数全体の集合として、Card(R)をたんにRと書きます。1点目をxに取った時、2点目はx以上と仮定しても、一般性は失わないので、2点目はx以上とします。そうすると、1点目の取り方は、閉区間[0,b]の中の点の数だから、R個。それに対して2点目は、[x,b]の中のどれかの点だから、R通り。従って、R×R=R2が全場合の数(数?。と言うか、本当はやっちゃいけません)。
右図のように、座標を取って考えます。またここでは、Rを実数全体の集合として、Card(R)をたんにRと書きます。1点目をxに取った時、2点目はx以上と仮定しても、一般性は失わないので、2点目はx以上とします。そうすると、1点目の取り方は、閉区間[0,b]の中の点の数だから、R個。それに対して2点目は、[x,b]の中のどれかの点だから、R通り。従って、R×R=R2が全場合の数(数?。と言うか、本当はやっちゃいけません)。
一方、長さa以上に2点目を取ろうとすると、1点目は[0,b−a] の中の点の数だから、R個。それに対して2点目は、[x+a,b]の中のどれかの点だから、R通り。従って、R×R=R2がこの場合の数(本当はやっちゃいけません)。
よって確率は、R2/R2(もっとやっちゃいけません)で1。1.0?・・・駄目だこれは・・・。
2.反則気味解答の試み
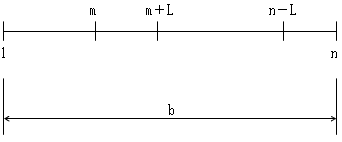 もう少しましに考えて、長さbの線分上に、有限個のn個の点が等間隔に並ぶとする。1点目をm番目の点とすると、2点目の取り方は、n−m+1通りあるから、
もう少しましに考えて、長さbの線分上に、有限個のn個の点が等間隔に並ぶとする。1点目をm番目の点とすると、2点目の取り方は、n−m+1通りあるから、
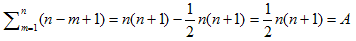
が全場合の数。一方、間隔L以上に2点目を取ろうとすると、n−m−L+1通りあって、1点目は、1〜n−Lの範囲だから、
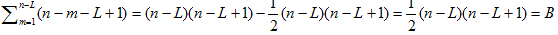
が、この場合の数。
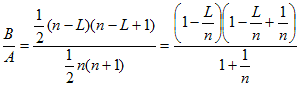
と変形して、n→∞(nにつられて、LもL→∞)の極限を取りたい。この時、
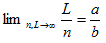
と仮定できるから、
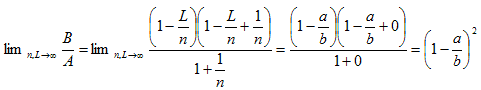
となる・・・今度はまともそう。以上は、長さbの線分を、可算無限分割したのと同じだから、少なくとも有理数までは行けた。後はこれを、実数まで延長してやれば良い。どうしたものか?。
3.大反則気味解答
2.の議論は、0≦a<bなる任意の有理数で成り立つ話で、関数、
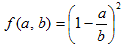
は、この範囲で連続だから、等式延長の原理より、実数範囲でも連続で、その収束先は唯一つ。
従って、任意の0≦a<bなる実数に対して、確率は、
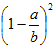
になる!。
・・・水の流れ先生、面積比を使う正解を教えて下さい。
NO.1822 確率は面積比[1](2) 2010.1.4. 夜ふかしのつらいおじさん
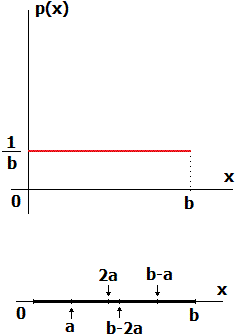
○長さbの線分上に1点をとるとき、どの点が選ばれるか差がないので、
点の取り方の確率分布p(x)は、一様で 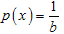 と考えられます。
と考えられます。
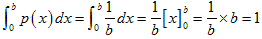
○長さbの線分上に2点A、Bを取ることを考えます。
点Aを先にとり、Bの位置によって2点間の距離が、a以上になる確率を考えます。
Aが座標(0)にあるときは、Bが(a)と(b)の間にあれば、2点間の距離がa以上になります。
確率は、長さに比例するとして、
その値は、 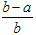 です。
です。
Aが座標(a)にあるときは、Bが(2a)と(b)の間にあれば、2点間の距離がa以上になります。
その確率は、 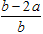 です。
です。
Aが座標(b-a)にあるときは、Bが(0)と(b-2a)の間にあれば、2点間の距離がa以上になります。
その確率は、 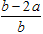 です。
です。
Aが座標(b)にあるときは、Bが(0)と(b-a)の間にあれば、2点間の距離がa以上になります。
その確率は、 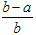 です。
です。
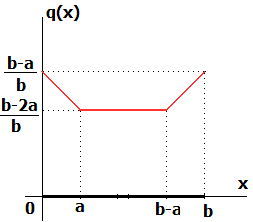 以上から、Aの位置ごとのBの取り方による確率分布q(x)は、
以上から、Aの位置ごとのBの取り方による確率分布q(x)は、
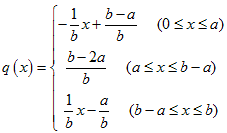
○よって求める確率は、
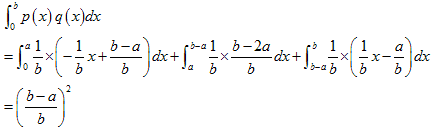
NO.1821 分割の問題(4) 2010.1.4. スモークマン
問題1
n本の直線で分けられる平面の数を f(n) で表わす。
f(0)=1,f(1)=2,f(2)=4,・・・
n本目の直線は (n-1)本の直線によって n個に分割され、その増加した直線に対応し
た分だけ新たな平面が増えているので...
f(n)=f(n-1)+n
f(1)-f(0)=1
f(2)-f(1)=2
・
・
・
f(n)-f(n-1)=n
つまり...
f(n)-f(0)=n(n+1)/2
f(n)=n(n+1)/2+1
=(n2+n+2)/2
問題2
同様に...
f(0)=1,f(1)=2,f(2)=4,f(3)=8,・・・
n個目の円は、それまでの (n-1)個の円と 2(n-1)個の交点をもち、2(n-1)個の線分に
分割されるので...新たな平面はその分だけ増える。
f(n)=f(n-1)+2(n-1)・・・n≧1
f(2)-f(1)=2
f(3)-f(2)=4
・
・
・
f(n)-f(n-1)=2(n-1)
つまり...
f(n)=2(1+2+3+・・・+(n-1))+2
=n(n-1)+2
=n2-n+2
f(0) は特異点・・・?
問題3
平面1枚で2分割
2枚で交線1本で平面は新たに2分割された分だけ増える+2
3枚目の平面は、2本の交線をもつので、最大で1個の交点をもち、
2*2分割される。+4
k枚目の平面は、k-1本の交線をもつので、
上から、k枚目の平面は
f(k-1)=((k-1)2+(k-1)+2)/2
=(k2-k+2)/2 に分割され、その分だけ空間の分割が増える。
f(0)=1
f(1)-f(0)=1
f(2)-f(1)=2
f(3)-f(2)=4
f(4)-f(3)=7
・
・
・
f(k)-f(k-1)=(k2-k+2)/2
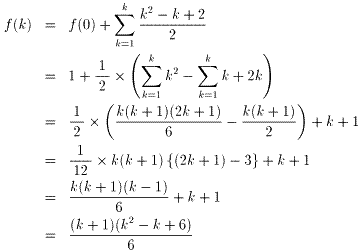
NO.1820 分割の問題(2) 2010.1.4. 夜ふかしのつらいおじさん
問題1
直線を増やすと領域の個数がどのように増えるか考えます。
どの2本の直線も平行でないように、直線を増やしていきます。
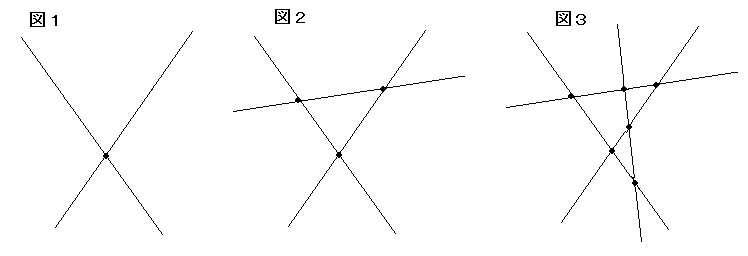
直線の個数をL、交点の個数をP、領域の個数をSで表します。
| L | P | S |
|---|
| 1 | 0 | 2
|
| 2 | 1 | 4
|
| 3 | 3 | 7
|
| 4 | 6 | 11
|
| 5 | 10 | 16
|
| ・・・ | ・・・ | ・・・
|
| n | 1/2×n(n-1) | 1/2×n(n+1)+1
|
直線が1本増えると、既にある直線すべてと交わるので交点は、既にある直線と同じ数だけ増えます。
直線が全部でn本あるときの交点の個数をP(n)とすると、
P(n)=P(n-1)+(n-1) ・・・ (A)
P(1)=0
P(2)=P(1)+1
P(3)=P(2)+2
・・・
P(n)=P(n-1)+n-1
∴ P(n)=1/2×n(n-1)
直線が1本増えると、既にある直線すべてと交わるので領域は、既にある直線より1つ多い数だけ増えます。
直線が全部でn本あるときの領域の個数をS(n)とすると、
S(n)=S(n-1)+(n+1)
S(1)=1+1
S(2)=S(1)+2
S(3)=S(2)+3
・・・
S(n)=S(n-1)+n
∴
S(n)=1/2×n(n+1)+1
問題2
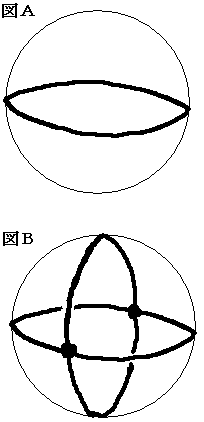
球面に1つの大円をかくと2個の領域に分かれます。(図A)
さらにもう1つ大円をかくと4個の領域に分かれます。
この2つの大円は2カ所で交わります。(図B)
すでにかかれた大円上の点から別の大円をかき始めます。
すると、その点にもどってきます。
すでにk個の大円がかかれているとします。
新たに大円をかけば、2k個の他の大円との共有点を持ちます。
f(k)をk個の大円がかかれているときの領域の個数とします。
f(1)=2+0×2
f(2)=f(1)+1×2
f(3)=f(2)+2×2
f(4)=f(3)+3×2
・・・・
f(n)=f(n−1)+(n−1)×2
これらを全部加え、左右で同じ値を消していくと、
f(n)=2+2×(1+2+3+4+・・・+n−1)
=n(n−1)+2
問題3
平面を増やすと領域の個数がどのように増えるかを考えます。
どの2つの平面も平行でなく
平面の交わりでできるどの2つの交直線も平行でないように、平面を増やしていきます。
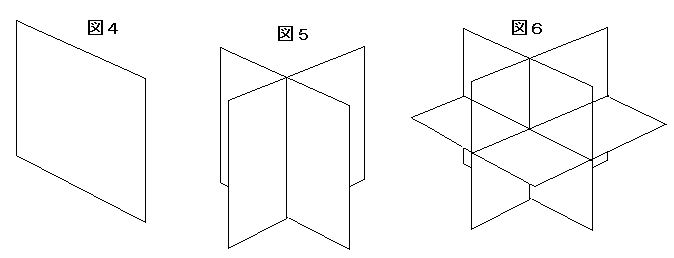
平面の個数をF、交直線の個数をL、交直線の交点の個数をP、領域の個数をTで表します。
| F | L | P | T |
|---|
| 1 | 0
| 0 | 2
|
| 2 | 1
| 0 | 4
|
| 3 | 3
| 1 | 8
|
| 4 | 6
| 4 | 15
|
| 5 | 10
| 10 | 26
|
| ・・・ | ・・・
| ・・・ | ・・・
|
| n | 1/2×n(n-1)
| 1/6×(n-2)(n-1)n | 1/6×(n+1)(n2-n+6)
|
平面が1枚増えると、既にある平面と交わるので、交直線は、既にある平面の個数だけ増えます。
平面が全部でn枚あるときの交直線の個数をL(n)とすると、
L(n)=L(n-1)+(n-1)
これは問題1の(A)と同じ漸化式なので、
L(n)=1/2×n(n-1)
平面が1枚増えると、既にある交直線と交わるので、交点は、既にある交直線の個数だけ増えます。
平面が全部でn枚あるときの交点の個数をP(n)とすると、
P(n)=P(n-1)+L(n-1)
P(1)=0
P(2)=P(1)+0
P(3)=P(2)+1/2×1・2
P(4)=P(3)+1/2×2・3
P(5)=P(4)+1/2×3・4
・・・
P(n)=P(n-1)+1/2×(n-2)(n-1)
∴ P(n)=1/6×(n-2)(n-1)n
さて、いよいよ領域の個数を数えます。
F=3のときまでは、苦労なく数えられます。
F=2からF=3にかけて、新たに追加した平面内に、交直線が2本、交点が1個あります。
これは図1の様子と同じです。
増えた領域は、図1の領域の個数(平面の)と同じです。
F=3からF=4にかけて、新たに追加した平面内に、交直線が3本、交点が3個あります。
これは図2の様子と同じです。
増えた領域は、図2の領域の個数(平面の)と同じです。
F=4からF=5にかけて、新たに追加した平面内に、交直線が4本、交点が6個あります。
これは図3の様子と同じです。
増えた領域は、図3の領域の個数(平面の)と同じです。
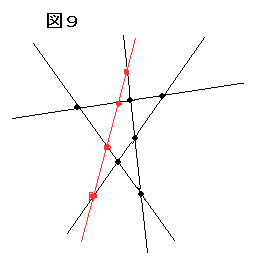
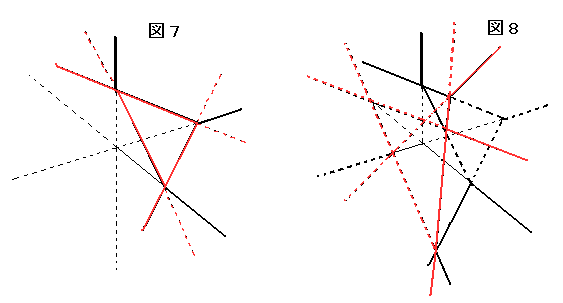
このあと平面を増やすと、その平面内で交直線と交点は図9のように増えます。
結果だけみると、既にある交直線のすべてと交わるように新たな直線を引いたようになります。
領域は、その図で分割された領域の個数増加します。
平面が全部でn枚あるときの領域の個数をT(n)とすると、
T(n)=T(n-1)+S(n-1)
T(1)=2
T(2)=T(1)+S(1)=T(1)+1/2×1・2+1
T(3)=T(2)+S(2)=T(2)+1/2×2・3+1
T(4)=T(3)+S(3)=T(3)+1/2×3・4+1
T(5)=T(4)+S(4)=T(4)+1/2×4・5+1
・・・
T(n)=T(n-1)+S(n-1)=T(n-1)+1/2×(n-1)・n + 1
∴ T(n)=1/6×(n+1)(n2-n+6)


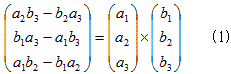
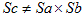
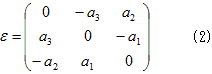
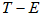
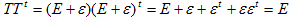
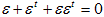
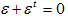
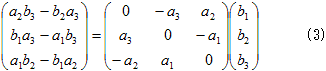
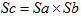
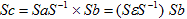
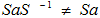
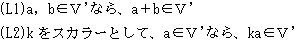
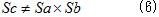
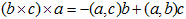

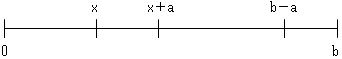 右図のように、座標を取って考えます。またここでは、Rを実数全体の集合として、Card(R)をたんにRと書きます。1点目をxに取った時、2点目はx以上と仮定しても、一般性は失わないので、2点目はx以上とします。そうすると、1点目の取り方は、閉区間[0,b]の中の点の数だから、R個。それに対して2点目は、[x,b]の中のどれかの点だから、R通り。従って、R×R=R2が全場合の数(数?。と言うか、本当はやっちゃいけません)。
右図のように、座標を取って考えます。またここでは、Rを実数全体の集合として、Card(R)をたんにRと書きます。1点目をxに取った時、2点目はx以上と仮定しても、一般性は失わないので、2点目はx以上とします。そうすると、1点目の取り方は、閉区間[0,b]の中の点の数だから、R個。それに対して2点目は、[x,b]の中のどれかの点だから、R通り。従って、R×R=R2が全場合の数(数?。と言うか、本当はやっちゃいけません)。 もう少しましに考えて、長さbの線分上に、有限個のn個の点が等間隔に並ぶとする。1点目をm番目の点とすると、2点目の取り方は、n−m+1通りあるから、
もう少しましに考えて、長さbの線分上に、有限個のn個の点が等間隔に並ぶとする。1点目をm番目の点とすると、2点目の取り方は、n−m+1通りあるから、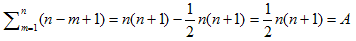
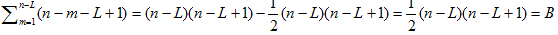
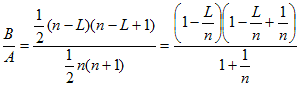
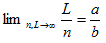
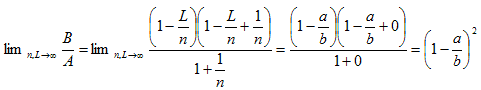
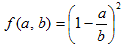
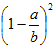
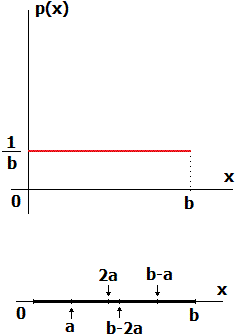
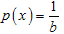 と考えられます。
と考えられます。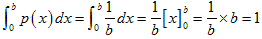
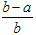 です。
です。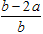 です。
です。 以上から、Aの位置ごとのBの取り方による確率分布q(x)は、
以上から、Aの位置ごとのBの取り方による確率分布q(x)は、