幅が一定値a(a=30)の平行線が何本かひいてあります。ここの長さl(lengthの頭文字)の針を落とします(l≦a)。針が平行線と交わる確率pは、
p=2l/aπ・・・(*)
となります。
ですから逆に、針が平行線と交わる確率pを統計的に求めれば、 円周率πの値が求められるというわけです。
(*)p=2l/aπ について
針が平行線と交わるのは、どういう条件が成立した場合なのかを考えてみます。
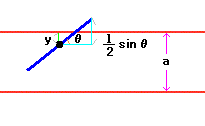
上の図のように、針を平行線のなす角をθ、 針の中心点から最も近い平行線までの距離をyとします。 このとき、
0≦y≦a/2、0≦θ≦π
であり、針と平行線が交わるのは、
y≦(l/2)sinθ
が成立するときです。
上のグラフでいうと、ブルーの部分が、針と平行線が交わる場合です。 ですからこのグラフの面積比から針と平行線が交わる確率を求めることができるわけです。
針と平行線が交わる確率p=(ブルーの部分の面積)/(長方形の面積)
(長方形の面積)=(a/2)×π=aπ/2
(ブルーの部分の面積)= 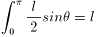
従って、
針と平行線が交わる確率p=2l/aπ・・・(*)
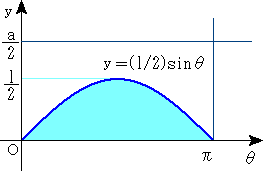
 戻る
戻る