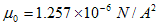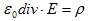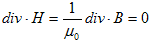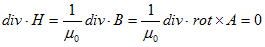NO.1761 電磁気学Minimum-2(磁気現象) 2009.1.10. DDT
以後、ベクトル解析Minimum-1,2,3,4の式は、無条件に使います。
磁気現象の研究が、磁石の研究、すなわち静磁気現象から始まったのは、まぎれもない事実です。そこでは静電現象におけるものと全く同じ、点磁荷に対するCoulombの法則が成り立ちます。当初磁力は、電気力とも重力とも違う力と思われ、静電気力の発生源としての電荷にC という独立な単位が与えられたように、磁荷にもwb(ウェーバー)という、他の単位とは独立な単位が与えられました。しかし後に、磁気現象は電気現象と無関係でない事が、 やBiot-Savartらによって発見されます。この時点で単位wbは、Cと供にある従来単位で書き換えられるべきものとなります。よって以下に述べる静磁気現象の項は、理論構成上は磁場の概念を与えるためだけに存在します。
やBiot-Savartらによって発見されます。この時点で単位wbは、Cと供にある従来単位で書き換えられるべきものとなります。よって以下に述べる静磁気現象の項は、理論構成上は磁場の概念を与えるためだけに存在します。
1.磁場の概念
経験的に磁極の存在はわかっています。磁極とは典型的には、棒磁石のN極とS極です。実験系のスケールに対して十分細長い棒磁石を用いる事により、棒磁石の両端の拡がりを持たない磁極、すなわち点磁荷の概念が得られます。
点磁荷に対する実験結果が、磁場に対するCoulombの法則です。
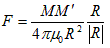 (1)
(1)
(1)で、MとM'は、位置ベクトルrとr'にある点磁荷で、R=r−r'です。μ0は、真空の透磁率と呼ばれる定数で、FはMとM'の間に働く力です。もちろん実際には、実験系のスケールに対して十分細長い棒磁石(もちろん動いてない)などを用意します。
磁力は当初、重力や電気力などとは違う力とみなされていました。そうすると磁荷は新しい力の発生源です。従って、力Fや距離R,電荷Qの単位の組み合わせで磁荷の単位を定義できません。磁荷に対して新しい単位wb(ウェーバー)を導入します。ただしwbの規格化、つまり何を1wb とするかは、任意に行えます。それが次の定義で、μ0の値は実験によって決まります。
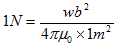 (2)
(2)
(2)より、透磁率の単位と値(実験による)が決まります。
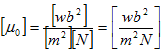
磁荷には符号のある事がわかっています。(1)のFをM'がMに及ぼす力とみなすと、ベクトルRの方向より、MとM'が同符号なら斥力,異符号なら引力です。電場のときに行ったのと同様に、(1)の力Fを磁荷Mで規格化し、M'による磁場を定義します。
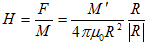 (3)
(3)
磁場の概念のもとでの相互作用のイメージも、電場の場合と同様です。MもM'も静止している場合、磁場Hを用いるか、Coulomb力Fを用いるかは、考え方の違いに過ぎません。しかし変動する磁気現象を扱うようになると、Coulombの法則は成り立ちませんが、磁場の概念は有効です。
磁場の単位は明らかに、
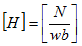
です。
2.ベクトルポテンシャルと磁場
電磁気学Minimum-1の伝で行くと、このあと静磁気現象を記述する静磁気ポテンシャルψ、
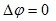
を導入し、これから静磁気ポテンシャル → 静磁気のCoulombの法則 → 点磁荷のCoulombの法則 → 静磁気ポテンシャルに戻る、という議論になります。ところで上式の右辺で、電荷密度に相当する磁荷密度が0になっているのは、物質としての磁荷は存在しないとわかったからです(少なくとも古典論では)。つまり静磁気ポテンシャル → 静磁気のCoulombの法則 → 点磁荷のCoulombの法則 → 静磁気ポテンシャルに戻る、という議論をしても、それは現象論に過ぎない事になります。この方向では、棒磁石の両端の磁極などを、現象論的に磁荷として扱いうるだけです。実験によれば、磁場は磁荷という実在から発生するのではなく、電流によって発生します。電流とは動く電荷なので、一般的に静磁気現象は動磁気現象の特殊ケースになります。これが静磁気現象を、これ以上やらない理由です。
実験によれば、電流によって発生する磁場は、ベクトルポテンシャルAと電流密度jによって記述でき、その法則は、
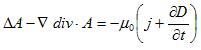 (1)
(1)
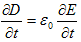
で与えられます。Aはベクトルです。(1)のμ0は真空の透磁率で、jは電流密度と呼ばれ、
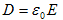
は、真空の電気変位と呼ばれます。ここでEは電場ですが、もはや静電場ではありません。Eは時間的に変動しうるので、
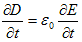
が意味を持ち、これは変位電流と言われます。Eは静電場でないにも関わらず、静電場の場合と同じように定義して良い事は、後で述べます。電流密度とは次のものを指します。電荷密度ρが速度vで移動するとき、
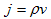
と書いて、電流密度と言います。ここでvはベクトルであり、jもベクトルです。jの単位は、
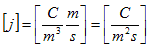
です。
Sをある曲面として、
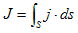
で定義されるベクトルを、Sから流れ出す電流と言います。Jの単位はC/sですが、この次元をAmpare(アンペア)と言い、以後単位Aで表わします。
Sを閉曲面とすると電流は、Sで囲まれた体積Vからの電荷の流出速度を表わしているので、これはVに含まれる電荷量の変化速度に等しくなります。
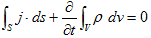
Gaussの発散定理を適用すれば、
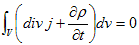
ですが、Vは任意に小さくできるので、
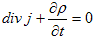 (2)
(2)
が必要です。(2)を電荷の保存則と言います。
ここでは、(1)の基になったBiot-Savartの法則を(1)から導き、逆にBiot-Savartがあれば、(1)に戻れる事を示します。最初に、ベクトル解析の公式、
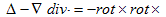
に注意すると、(1)は、
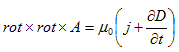
と書き直せます。磁束密度Bと磁場Hを、
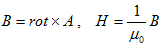 (3)
(3)
で定義すると、
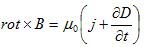 (4)
(4)
となります。これを (アンペール)の法則と言います。次に、これらの単位は、
(アンペール)の法則と言います。次に、これらの単位は、
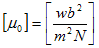 (5)
(5)
でしたが、
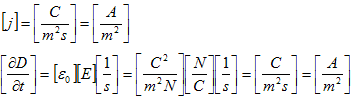
より、
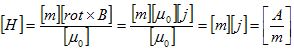 (6)
(6)
です。ところが、ここで定義した磁場Hは、電流の流れ方を調整する事で静磁場にする事ができ(できる事は後で示します)、その場合、1.で述べた静磁場と全く同じ性質を示すことも、実験的に確認されています。
従って、1.より、
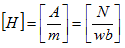
でなければなりません。これで、wbの次元が決まります。
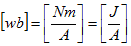
です。これを(5)に代入すれば、
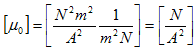 (7)
(7)
が得られ、透磁率の単位が決まります。さらに(7)から、
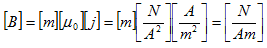 (8)
(8)
となって、磁束密度の単位も得られます。最後に、ベクトルポテンシャルの単位は、
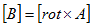
である事から、
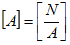 (9)
(9)
がわかります。一方、静電現象の場合、電場Eと静電ポテンシャルφの次元は、
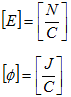
でした。静電現象と磁気現象とは、完全に同じではありませんが、[m]×B→E,[m]×A→φ,A→C という対比は可能です。[m]×B→Eより、磁気現象においては、静磁気現象を通じて定義された磁場Hより、電流との関連で定義された磁束密度Bの方がより本質的であり、[m]×A→φより、ベクトルポテンシャルは静電ポテンシャルと同じ立場にあり、A→C より電流(A)が真の磁荷に相当している(電流は電子の運動だから、磁荷は存在しないけれど)、という事が見て取れます。
3.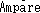 の法則からBiot-Savartの法則へ
の法則からBiot-Savartの法則へ
Biot-Savartは「ビオ・サバール」と読みます。実験的にBiot-Savartの法則は、電気変位が時間変化しない、すなわち定常電流の場合に導かれました。電気変位が時間変化しないとは、2.(1)の2つ目の式で、
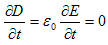
となる事を意味します。しかし電場Eが時間的に一定な静電場であっても、その中に置かれた荷電粒子e(電子)は加速します。何故ならCoulombの法則より、荷電粒子eは一定の力、
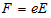
を受け続けるからです(電磁気学Minimum-1の結果)。電子の流れが電流になる事は、ご存知と思いますが、そうすると2.(1)の1番目の式の中で、
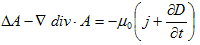 (1)
(1)
の電流密度jは時間的に変化し続け、とても定常電流とは言えない事態になります。j=ev だからです。ここでBiot-Savartの法則は、じつは電線に対して得られたものだった、という事実が登場します。

図-1
電線の中に時間的に変化しない電場Eを与える事は、電池を電線につなげば容易に実現できます。それによって電線(金属)の中の自由電子は加速しますが、電線の中には電子にとってみれば、走行を邪魔する原子や原子核がそこら中に存在します。それらへの衝突によって、電子は運動エネルギーを奪われ、電線全体としてはその摩擦によって発熱します。これがオームの法則です。そして摩擦力と電場による加速力が釣り合った時点で、電線の電子集団全体は、ほぼ一定の速度を(電流を)保ちます。これもオームの法則です。これが2.(1)において、j=一定,∂D/∂t=0 としても良い根拠です。そうすると(1)は、
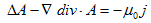 (1)
(1)
となりますが、上記を満たすAを求めるために、
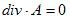 (2)
(2)
という付加条件を付けます。この条件を付けても一般性の失われない事は、後で述べます。
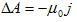 (3)
(3)
が、(2)の条件のもとでの(1)です。
Aはベクトルである事を強調しておきます。そしてΔは、スカラー作用素です。よって、ΔA=−μ0j とは、
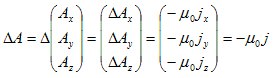 (4)
(4)
の事です。Aまたはjの各成分に対して、静電現象のΔφ=−ρ/ε0 と同じタイプの式になります。同じタイプの式なので、同じように処理できます。(4)の各成分を、Aα,jα で表わします。最初に、電場について行ったように、大きさ|J|の点電流J=(Jx(r'),Jy(r'),Jz(r'))を導入したいのですが、これでは不十分なのがわかります。何故なら、
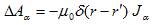
を考えると、μ0.δ,Jの単位は、N/A2,1/m3,A で、3つかけると、N/A/m3 となりますが、ΔAの単位は、N/A/m2 だからです。つまり長さの次元が一個足りません。電流密度の定義のせいです。そこで電流素、
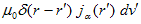
を考えます。これによって(4)の各成分は、
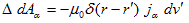
と書けます。ここでベクトルポテンシャルの成分に記号d をつけた事に悩まないで下さい。こんなのはただの記号です。後で見映えが良いので、こう書くだけですし、どんな記号を使おうと意味は変わりません。上記の解は、静電現象の点電荷の場合と全く同じく、
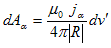 (5)
(5)
で得られます。ただしR=r−r' です。(5)をベクトル的にまとめれば、
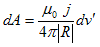 (6)
(6)
となるのは明らかだと思います。
後は電流密度j(r') が、そこら中に連続して分布する場合、Δの線形性から(6)を使って、
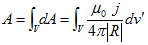 (7)
(7)
となるのに気づくだけです。ねっ!、見映えが良いじゃないですか?。
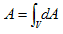
と書けるんですから。
一方、電線の断面積をa,そこを流れる電流密度をj,電線の線素をdL' とすると、
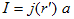
は、位置r'にある電線の断面上の電流ですが、電線が十分細いとすると、点電流とみなせます。線素dL' に存在する定常電流の合計IdL' を考えれば、それが上で定義した電流素、
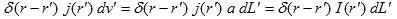
になるのは明らかです。これによって生じるベクトルポテンシャルは、(7)を使って、
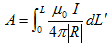 (8)
(8)
と書けます。ここでLは図-1の電線の長さです。これより磁場Hは、rotがrに作用する事に注意して、
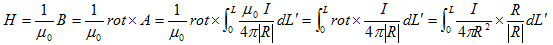 (9)
(9)
となりますが、これこそが実験的に得られるBiot-Savartの法則です。
ところで付加条件(2)より、
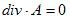 (10)
(10)
でなければなりません。このdiv もr に作用します。
(10)を示します。(8)より、
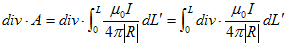 (11)
(11)
です。最右辺で、r' の関数であるI(r') は、電線上の定常電流なので、位置r' によらない定数である事、また|R|=|r−r'| が符号を除いて、rとr' に関して対称になっている事に注意すると、r' に作用するdiv をdiv' と書く事にして、
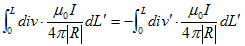 (12)
(12)
が成り立ちます。
(12)の右辺にGaussの発散定理を適用しますが、その際に、IdL' をj dv' の表現に戻し、積分領域V(ε)を、電線を内部に含むような半径εの十分大きな球とします。電線の外でj=0 と考えれば、こうしても問題ないはずです。すると、
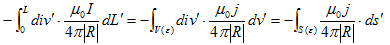
です。
上記の最右辺で、Rのr' はV(ε)の表面S(ε)に束縛されたベクトルで、|R|は、r からS(ε)までの距離によって変化します。しかしε→∞ の極限では(これは勝手に出来ます)、rの位置によらず、|R|→εとなり定数です。従って、
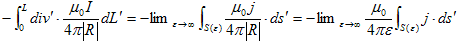 (13)
(13)
が得られます。(13)の最右辺に再びGaussの発散定理を適用し、さらに電荷の保存則2.(2)も適用すれば、
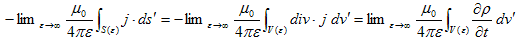 (14)
(14)
となりますが、V(ε)の電線領域内部ではρは定数(j=ρv で、jは定常電流密度,v=一定)で、電線外ではρ=0 でした。
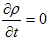
です。よって、
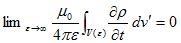 (15)
(15)
が得られます。以上より、(15),(14),(13),(12),(11)とたどれば、
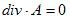
とわかります。以上により(1)の解(8)は、div・A=0 の必要十分条件になりますが、(1)の解が(8)以外にない事はまだ示していません。そこでdiv・A=0 を仮定しない場合の解を、
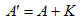 (16)
(16)
とします。右辺のAは(8)です。(16)を(1)に代入すれば、Δ,∇,div の線形性と、Aが(3)を満たす事から、
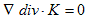 (17)
(17)
です。(17)を∇で積分すれば、
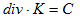
となります。Cはスカラーの積分定数です。上記を任意の体積で積分し、Gaussの発散定理を用いれば、
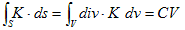 (18)
(18)
です。ここで最右辺のVは積分領域の体積を表わします。一方、積分領域の表面積Sは、外法線方向の単位ベクトルをn,面素をda として、
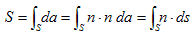
と書けます。これより(18)は、
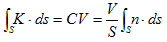
と変形でき、
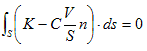
が得られます。積分領域Vは任意だったので、V→0 の極限で考えれば、
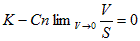
ですが、体積Vと表面積Sの間には、
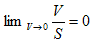
の関係があるので、
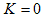
になります。(1)の解は、(8)だけです。
4.Biot-Savartの法則から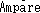 の法則へ
の法則へ
逆に3.(9)でIdL' はさっきやったように、電流密度と微小体積の積の電流素、j dv' と考えられます。
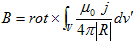 (1)
(1)
ここでVは、jが存在する体積で、jは定常電流密度です。両辺に、rに作用するrotをかけ、
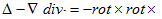
を考慮すれば、
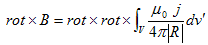 (2)
(2)
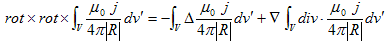 (3)
(3)
となります。
(3)の1項目は、静電ポテンシャルの時にやったように、
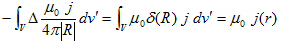 (4)
(4)
となり、2項目もさっきやったように、Vを含む十分大きな球V(ε)を考え、ε→∞の極限で計算すれば、jが定常電流密度という事から、
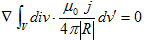 (5)
(5)
が得られます。
従って、(2),(3),(4),(5)から、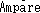 の法則、
の法則、
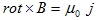 (6)
(6)
が再び出てきます。さらに、(1)のdiv をとれば、div・rot×=0 である事から、
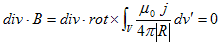
となるので、適当なベクトルポテンシャルAのもとに、
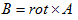
と書ける事になります。これを(6)に代入すれば、
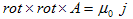
となるので、Δ−∇div・=−rot×rot×より、
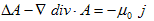
となり、変位電流がない場合の2.(1)、すなわちBiot-Savartの法則から直接導かれる、磁気現象の基本法則に戻れます。
5.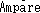 の法則への変位電流の導入
の法則への変位電流の導入
実験的に得られる 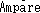 の法則は4.(6)であり、2.(4)ではありません。変位電流の存在はMaxwellにより、次のように予想されました。
の法則は4.(6)であり、2.(4)ではありません。変位電流の存在はMaxwellにより、次のように予想されました。
4.(6)において、変位電流が存在する場合の差を、
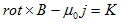 (1)
(1)
と書きます。両辺のdivをとる事により、
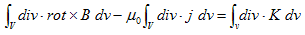
を得ますが、div・rot×=0 である事と、電荷の保存則2.(2)より、
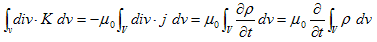 (2)
(2)
となります。電荷密度ρは速度vで動くし、時間的にも変化するとみなすにも関わらず、ここでも静電荷の保存則が有効だとすれば、(2)は、
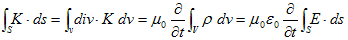
となりますが、Sは任意に小さくとれるので、
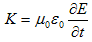
が必要になります。従って(1)は、
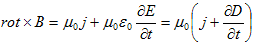 (3)
(3)
と予想されます。
(3)をそのまま受け入れるには、1つ問題があります。(3)の前提は、変位電流のない場合の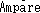 の法則2.(4),電荷の保存則2.(2),静電荷の保存則です。これらの内2.(4)は実験事実で、2.(2)は数学的定義に過ぎないので問題ないと思われます。問題なのは静電荷の保存則です。これも実験事実ではありますが、静電現象の実験事実に基づいて導かれたものでした。ところが変位電流の存在とは、
の法則2.(4),電荷の保存則2.(2),静電荷の保存則です。これらの内2.(4)は実験事実で、2.(2)は数学的定義に過ぎないので問題ないと思われます。問題なのは静電荷の保存則です。これも実験事実ではありますが、静電現象の実験事実に基づいて導かれたものでした。ところが変位電流の存在とは、
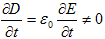
という事で、まさしく静電場(静電荷)ではない場合です。静電現象でない現象に、静電現象の結果を用いて良いかどうかは、実験を待つ必要があります。そのためには、変動する電場を含むような現象が必要でした。それこそが電磁場だったのです。実験はMaxwellを支持しましたが、これで、この自習ノートの決着も見えて来ます。つまり電磁場の存在を導けたら、そこで一応の完結です。しかし電磁場の存在を言うためには、Faradayの電磁誘導の法則が必要です。
6.磁石との関係,静磁気現象
現在では磁石の振る舞いは、磁石を構成する原子集団の電子の運動の集団的性質で説明されています。磁石も含めた安定した物質は、全て定常状態にあると考えられます。よって磁石の中の電子の運動も定常状態で、磁石の磁力は定常電流に基づいて説明できる事になります。定常電流なので、定常電流に基づいた実験結果Biot-Svartの法則を、そのまま適用できる事になります。
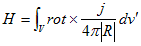 (1)
(1)
(1)の右辺に、rotの積の微分公式、rot×(kA)=∇k×A+k rot×Aを適用します。jはrot に対して定数なので、
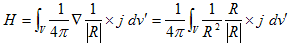 (2)
(2)
が得られます。ここで磁石を構成する原子の半径程度の球をV(ε)とし、電子eがその中の円軌道を回転していると考えます。原子半径は非常に小さく、電子eがVの中でつくる電流素の値 |j| dv' は、電子の電荷が離散値なので、その値はいかに小さかろうとやはり離散値です。これはδ関数で表わすべきものです。その値を、
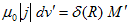
で表わすと、(2)はδ関数の性質から、
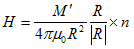 (3)
(3)
と表わされ、静磁気現象から得られるCoulombの法則、
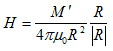 (4)
(4)
とほぼ同じものになります。(3)のnは、各瞬間の電子の運動方向の単位ベクトルです。(4)のHは等方的ですが、(3)はnに対して方向性を持ちます。しかし電子が円軌道を高速で回るとすれば、平均的には、(3)のnに関する方向性もなくなると予想できますが、完全な説明には、物質の構成理論(物性論)が必要です。真空の透磁率μ0の値は、1.(2)の定義を用いて(4)を実験にかければ求めることが出来きます。
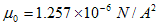
となります。
巨視的な磁石の性質から、重要な実験事実が導かれます。電荷の場合、単独の電荷が存在する事とCoulombの法則から、
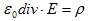
が導かれましたが、磁荷の場合は常に、
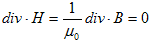
となります。この事は、単独の磁荷とは仮想的なものであり、磁気単極子が存在しない事を意味します。磁荷の概念が有効なのは、磁石のN極とS極といった巨視的現象においてのみです。これに対する実験事実は次のようになります。
ある棒磁石を際限なく分割しても、常にその両端にはN極とS極がペアで現れ、単独のN極やS極は決して存在せず、予想される分割の極限においても、それらは磁気双極子としてのみ現れる。
ベクトルポテンシャルを用いれば、
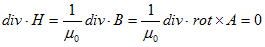
は恒等式なので、この事は磁場(磁束密度)の定義の中に含まれています。
7.まとめ
今回も、一般法則 → 実験事実 → 一般法則 というスタイルでやってみましたが、やってみて思いました。電磁気学って敷居が高いです。
まず冒頭のベクトルポテンシャルに関する法則を述べるだけで、変位電流の定義,電流と電流密度の定義,磁束密度と磁場の定義が必要になる上に、静磁場との関係も入ってきて、ここでは一回単位を整理しないと、前に進めない状態でした。
次に点電流に関するラプラス方程式を、静電現象にならって解こうと思ったら、今度は電流密度とδ関数の次元の相性の悪さが出てきて、電流素で考えないと上手くいかない事に気づくのに、しばらくかかりました。
しかもラプラス方程式にするためには、ベクトルポテンシャルに関する補助条件div・A=0 も必要でした。これは定常電流に関して導ける性質で、Biot-Savartの実験の前提になるのが後でわかりました。
参考文献ではこの点に関して、1行半くらいの説明で上手に身をかわしていて、ΔA=−μ0j を解き終わった後では2度とベクトルポテンシャルを使わないで、後は磁束密度Bだけで話を進めるという方針を採っていましたが、終始Aを前面に押し出してやってみると、div・A=0 は自明でない事がわかり、これを導くのにはけっこう考えました。まぁ、やり方が悪いのかも知れませんが・・・。
[参考文献]
[1] 現代物理学叢書,電磁力学,牟田泰三,2001年,岩波書店.
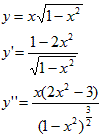
 やBiot-Savartらによって発見されます。この時点で単位wbは、Cと供にある従来単位で書き換えられるべきものとなります。よって以下に述べる静磁気現象の項は、理論構成上は磁場の概念を与えるためだけに存在します。
やBiot-Savartらによって発見されます。この時点で単位wbは、Cと供にある従来単位で書き換えられるべきものとなります。よって以下に述べる静磁気現象の項は、理論構成上は磁場の概念を与えるためだけに存在します。
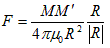 (1)
(1)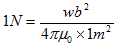 (2)
(2)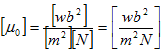
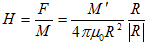 (3)
(3)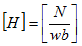
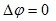
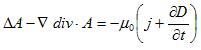 (1)
(1)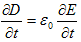
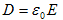
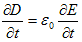
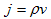
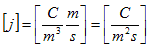
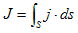
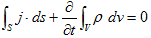
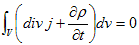
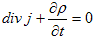 (2)
(2)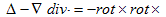
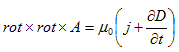
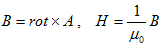 (3)
(3)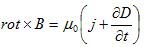 (4)
(4)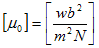 (5)
(5)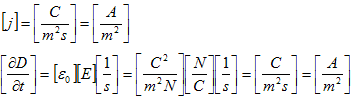
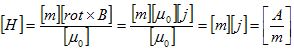 (6)
(6)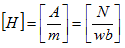
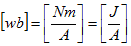
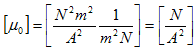 (7)
(7)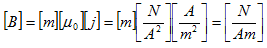 (8)
(8)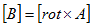
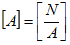 (9)
(9)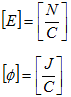
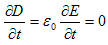
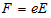
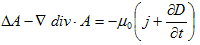 (1)
(1)
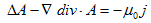 (1)
(1)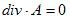 (2)
(2)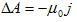 (3)
(3)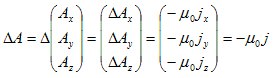 (4)
(4)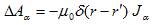
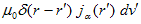
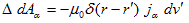
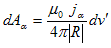 (5)
(5)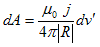 (6)
(6)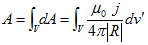 (7)
(7)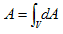
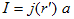
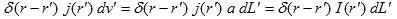
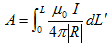 (8)
(8)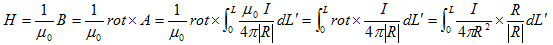 (9)
(9)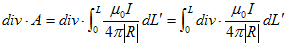 (11)
(11)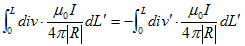 (12)
(12)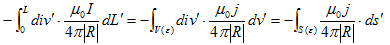
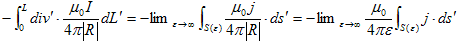 (13)
(13)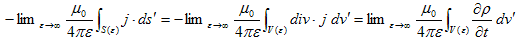 (14)
(14)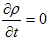
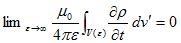 (15)
(15)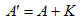 (16)
(16)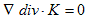 (17)
(17)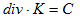
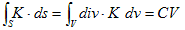 (18)
(18)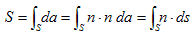
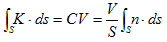
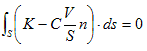
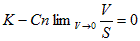
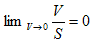
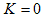
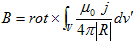 (1)
(1)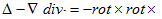
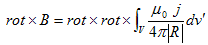 (2)
(2)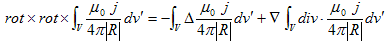 (3)
(3)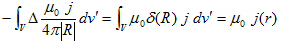 (4)
(4)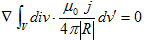 (5)
(5)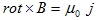 (6)
(6)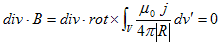
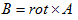
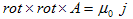
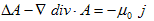
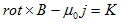 (1)
(1)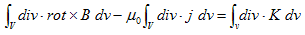
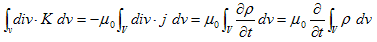 (2)
(2)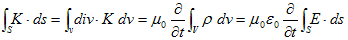
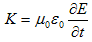
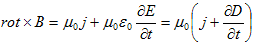 (3)
(3)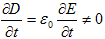
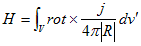 (1)
(1)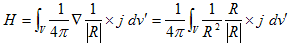 (2)
(2)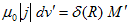
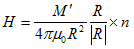 (3)
(3)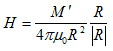 (4)
(4)