
Weekend Mathematics乛僐儘僉僂儉幒乛1998.7乣12乛NO.22
NO.168 丂丂丂 10/20 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮俋乯 崱擔偼堏摦擔偲偄偆偙偲偱丄擔杮僔儕亅僘偼偁傝傑偣傫丅
壗偲側偔椧偟偄側偁丒丒丒丅 偦偙偱丄巹偼偙傫側偙偲傪峫偊傑偟偨丅
偲偙傠偱崱夞偺擔杮僔儕亅僘偼丄
戞侾丄俀帋崌偑墶昹僗僞僕傾儉丄
戞俁丄係丄俆帋崌偑惣晲僪亅儉丄
偦偟偰戞俇丄俈帋崌偑嵞傃墶昹僗僞僕傾儉偱峴傢傟傞梊掕偩偦偆偱偡丅
乮枅擭丄偙偺僷僞亅儞偱椉僠亅儉偺儂亅儉媴応傪巊偆偺偱偟傚偆偐丠乯
傕偪傠傫戞俆帋崌埲崀偼丄帋崌偺棳傟偵傛偭偰偼傗傜側偄壜擻惈傕偁傞傢偗偱偡丅
扨弮偵帋崌悢偵斾椺偟偰僠働僢僩廂擖摍偑擖傞偲偟偰丄
墶昹僗僞僕傾儉偲惣晲僪亅儉偱偼偳偪傜偑摼偐丠
戞侾乣係帋崌傑偱偼妋幚偵峴傢傟傞傢偗偱丄偙偺晹暘偵偮偄偨偼俀帋崌
偯偮側偺偱暯摍偱偡丅幚巤偝傟傞壜擻惈偺崅偄戞俆帋崌傪侾偮偲傞偐丄
偦傟偲傕壜擻惈偼掅偔側傞傕偺偺戞俇帋崌偲戞俈帋崌偺俀偮傪偲傞偐丠
偁側偨側傜偳偆偟傑偡丠

NO.169 丂丂丂 10/21 丂丂悈偺棳傟 丂丂丂 1998僇亅僪偺栤戣乮侾乯 侾乣侾俋俋俉傑偱偺惍悢傪昞偵偐偄偨僇乕僪偑暲傋傜傟偰偄傞丅
偙偺僇乕僪偵慡偰昞偺忬懺偐傜偼偠傔偰師偺侾俋俋俉屄偺憖嶌傪
偡傞丅
憖嶌偑廔椆偟偨偲偒丄昞岦偒偵側偭偰偄傞僇乕僪偼壗枃偁傞偐丅
丒丒丒
丒丒丒

NO.170 丂丂丂 10/21 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮侾侽乯 崱擔偼塉偺偨傔偵擔杮僔儕亅僘偼偁傝傑偣傫丅巆擮丅
NO.168偱偺
墶昹僗僞僕傾儉偲惣晲僪亅儉偱偼偳偪傜偑摼偐丠偲偄偆榖偟偱偡丅
戞係帋崌傑偱偱寛拝偟偨応崌偲丄
戞俇帋崌傑偱偱寛拝偟偨応崌偼丄
偳偪傜偺媴応傕摨悢偺帋崌傪偙側偟偨偙偲偵側傞偺偱丄暯摍偱偡丅
戞俆帋崌傑偱偱寛拝偟偨応崌偼惣晲僪亅儉偑偍摼丄
戞俈帋崌傑偱傕偮傟偙傫偩応崌偼墶昹僗僞僕傾儉偑摼傪偡傞偲偄偆偙偲偵側傝傑偡丅
NO.163偱寁嶼偟偨傛偆偵丄
戞俆帋崌傑偱偱寛拝偡傞妋棪偼(1/4)丄
偦傟偵懳偟偰戞俈帋崌傑偱傕偮傟偙傓妋棪偼(5/16)偱偡丅
(1/4)亙(5/16)偱偡偐傜丄(1/16)偺嵎偱墶昹僗僞僕傾儉偺曽偑摼偩偲偄偆偙偲偵側傝傑偡丅
傕偪傠傫偙傟偼帋崌偑奐巒偝傟傞慜偺榖偟偱偡丅
偪傚偭偲堄奜偱偟偨丠
偟偐偟側偑傜媴応偺攝暘偼僩亅僞儖偱傒傞偲偐側傝懨摉側
暘偗曽偱偁傞偲偄偊傞偲巚偄傑偡丅

NO.171 丂丂丂 10/22 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮侾侾乯 偆亅傫丄巆擮丅
惣晲僪亅儉偵偆偮偭偰丄Bay Stars偼晄挷丄晧偗偪傖偄傑偟偨丅
巆擮丅 墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偱偡丅 廬偭偰丄墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偼丄
(1/4)+(1/4)+(3/16)=(11/16)偲側傝傑偡丅 師偵惣晲儔僀僆儞僘偑桪彑偡傞妋棪傪弌偟偰傒傑偡丅 廬偭偰惣晲儔僀僆儞僘偑桪彑偡傞妋棪偼丄
0+(1/8)+(3/16)=(5/16)偲側傝傑偡丅 師偵憤帋崌悢偺婜懸抣傪寁嶼偟偰傒傑偡丅
墶昹儀僀僗僞亅僘偑桪彑偡傞応崌偲惣晲儔僀僆儞僘偑桪彑偡傞応崌偲偑偁傝傑偡偐傜丄
偦傟偧傟偺妋棪傪懌偟偰丄帋崌悢偵偐偗偰懌偟偰偄偒傑偡丅
捠嶼惉愌偼儀僀僗僞亅僘偑俀彑丄惣晲偑侾彑偱偡丅
偙偺屻偺妋棪傪寁嶼偟偰傒傑偟偨丅
偙傟埲崀傕丄墶昹儀僀僗僞亅僘偲惣晹儔僀僆儞僘偺椡偑懳摍偲偟偰寁嶼偟傑偡丅
偍屳偄偵彑偮妋棪偼(1/2)偱丄晧偗傞妋棪傕(1/2)偱偡丅
帋崌悢係偺壜擻惈偼側偔側傝傑偟偨丅
乽仜仜亊仜仜乿偟偐偁傝傑偣傫丅
妋棪偼(1/2)2=1/4
乽仜仜亊仩仩仜乿偲側傝傑偡丅
俇帋崌栚偼昁偢仜偱丄俀偮偺仩偺拞偵侾屄偺仜偲侾屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)2亊(1/2)亊2俠1=1/4
乽仜仜亊仩仩仩仜乿偲側傝傑偡丅
俈帋崌栚偼昁偢仜偱丄俁偮偺仩偺拞偵侾屄偺仜偲俀屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)2亊(1/2)2亊3俠1=3/16
(11/16)=0.6875偱偡偐傜丄傑偩傑偩儀僀僗僞亅僘桳棙偱偡丅
偁傝偊傑偣傫丅
妋棪偼0
乽亊亊仜仜仜仜乿偟偐偁傝傑偣傫丅
妋棪偼(1/2)3=1/8
乽亊亊仜仩仩仩仜乿偲側傝傑偡丅
俈帋崌栚偼昁偢仜偱丄俁偮偺仩偺拞偵俀屄偺仜偲侾屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)3亊(1/2)亊3俠1=3/16
傕偪傠傫丄儀僀僗僞亅僘偑桪彑偡傞妋棪(11/16)偲
儔僀僆儞僘偑桪彑偡傞妋棪(5/16)傪懌偡偲1偵側傝傑偡丅
丂5亊(1/4+0)亄6亊(1/4+1/8)亄7亊(3/16+3/16)
亖5亊(1/4)亄6亊(3/8)亄7亊(3/8)
亖(1/8)亊(10+18+21)
亖(49/8)
亖6.125
偲側傝傑偡丅
帋崌偑屳妏偵恑峴偡傞偲丄憤帋崌悢偺婜懸抣偼憹偊傑偡丅

NO.172 丂丂丂 10/23 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮侾俀乯 俋夞棤丄儀僀僗僞亅僘偺峌寕偼偳偒偳偒傕傫偱偟偨偑丄
柍擮丄巆擮丅 墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偱偡丅 廬偭偰丄墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偼丄
(1/4)+(1/4)=(1/2)偲側傝傑偡丅 惣晲儔僀僆儞僘偑桪彑偡傞妋棪傕
乽亊亊仜仜仩仩乿
偲側傞偩偗偱丄摨條偱偡丅 師偵憤帋崌悢偺婜懸抣傪寁嶼偟偰傒傑偡丅
墶昹儀僀僗僞亅僘偑桪彑偡傞応崌偲惣晲儔僀僆儞僘偑桪彑偡傞応崌偲偑偁傝傑偡偐傜丄
偦傟偧傟偺妋棪傪懌偟偰丄帋崌悢偵偐偗偰懌偟偰偄偒傑偡丅
捠嶼惉愌偼儀僀僗僞亅僘偑俀彑丄惣晲傕俀彑丄崀傝弌偟偱偡丅
妋棪傪寁嶼偡傞昁梫偼偁傝傑偣傫偹丄屲暘屲暘偱偡丅
偱傕丄堦墳傗傝傑偟傚偆丅
偙傟埲崀傕丄墶昹儀僀僗僞亅僘偲惣晹儔僀僆儞僘偺椡偑懳摍偲偟偰寁嶼偟傑偡丅
偍屳偄偵彑偮妋棪偼(1/2)偱丄晧偗傞妋棪傕(1/2)偱偡丅
帋崌悢係丄俆偺壜擻惈偼側偔側傝傑偟偨丅
乽仜仜亊亊仜仜乿偟偐偁傝傑偣傫丅
妋棪偼(1/2)2=1/4
乽仜仜亊亊仩仩仜乿偲側傝傑偡丅
俈帋崌栚偼昁偢仜偱丄俀偮偺仩偺拞偵侾屄偺仜偲侾屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)2亊(1/2)亊2俠1=1/4
丂6亊(1/4+1/4)亄7亊(1/4+1/4)
亖6亊(1/2)亄7亊(1/2)
亖(1/2)亊(6+7)
亖(13/2)
亖6.5
偲側傝傑偡丅

NO.173 丂丂丂 10/24 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮侾俁乯 崱擔偺摼揰傪師夞偵巆偟偰偍偒偨亅偄両丂
偲偄偆埵偺妶桇偱儀僀僗僞亅僘偺埑彑偱偟偨丅(17-5) 墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偱偡丅 廬偭偰丄墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偼丄
(1/2)+(1/4)=(3/4)偲側傝傑偡丅 惣晲儔僀僆儞僘偑桪彑偡傞妋棪偱偡丅 師偵憤帋崌悢偺婜懸抣傪寁嶼偟偰傒傑偡丅
墶昹儀僀僗僞亅僘偑桪彑偡傞応崌偲惣晲儔僀僆儞僘偑桪彑偡傞応崌偲偑偁傝傑偡偐傜丄
偦傟偧傟偺妋棪傪懌偟偰丄帋崌悢偵偐偗偰懌偟偰偄偒傑偡丅
捠嶼惉愌偼儀僀僗僞亅僘偑俁彑丄惣晲偼俀彑偱偡丅
偙傟埲崀傕丄墶昹儀僀僗僞亅僘偲惣晹儔僀僆儞僘偺椡偑懳摍偲偟偰寁嶼偟傑偡丅
偍屳偄偵彑偮妋棪偼(1/2)偱丄晧偗傞妋棪傕(1/2)偱偡丅
乽仜仜亊亊仜仜乿偟偐偁傝傑偣傫丅
妋棪偼(1/2)
乽仜仜亊亊仜仜亊仜乿偲側傞応崌偱偡丅
妋棪偼(1/2)亊(1/2)=(1/4)
偁傝偊傑偣傫丅
妋棪偼0
乽亊亊仜仜亊仜仜乿偟偐偁傝傑偣傫丅
妋棪偼(1/2)2=(1/4)
丂6亊(1/2)亄7亊(1/4+1/4)
亖6亊(1/2)亄7亊(1/2)
亖(1/2)亊(6+7)
亖(13/2)
亖6.5
偲側傝傑偡丅
偙傟偼丄嶐擔偲曄傢傝傑偣傫丅
嶐擔偺抜奒偱怳傝弌偟偵栠偭偨傢偗偱偡偐傜丄
戞侾愴偑廔傢偭偨帪偲摨條偵憤帋崌悢偺婜懸抣偵偼曄壔偑偁傝傑偣傫丅
偝偁師偼偄傛偄傛桪彑傪偐偗偰墶昹僗僞僕傾儉偵栠偭偰偒傑偡丅

NO.174 丂丂丂 10/24 丂丂Junko 丂丂丂 1998僇亅僪偺栤戣乮俀乯 庼嬈偺拞偱丄廤崌俙亖{x|x偼係俉偺惓偺栺悢}偲偄偆傛偆側傕偺傪埖偆偙偲偑偁傝傑偡丅
偙偺廤崌偺梫慺傪嬶懱揑偵暲傋傞昁梫偑偁傞帪偵丄偙偆巜摫偟偰偄傑偡丅 偙偺栺悢偵偼昁偢偐偗偰丄
偦偺悢偵側傞儁傾偑懚嵼偡傞偲偄偆偺偑億僀儞僩偱偡丅
偮傑傝丄栺悢偺屄悢偼嬾悢偱偡丅 栤戣偵栠傝傑偡丅
n偑帺暘偺栺悢偺帪偺傒丄傂偭偔傝曉偝傟傞偙偲偵側傝傑偡丅
偲偙傠偑栺悢偼嬼悢屄側偺偱偡偐傜丄嵟廔揑偵偼昞岦偒偵側傝傑偡丅 侾乣侾俋俋俉傑偱偺拞偵暯曽悢偑偄偔偮偁傞偐丠丂偲偄偆偲丄
係係2亖侾俋俁俇偑嵟戝偱偡偐傜丄係係屄偱偡丅 摎偊丂侾俋俋俉亅係係亖侾俋俆係
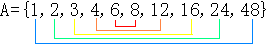
偲偄偆嬶崌偱偡丅
偙偆偡傟偽丄傕傟側偔扵偟弌偡偙偲偑偱偒傑偡丅
偦傟偱偼摎偊偼侾俋俋俉枃偐偲巚偄偒傗丄偦偆偱偼偁傝傑偣傫丅
椺奜偑偁傝傑偡丅
偦傟偼暯曽悢偱偡丅
暯曽悢偲偄偆偺偼丄壗偐帺慠悢偺俀忔偵側偭偰偄傞悢偱偡丅
椺偊偽丄廤崌俛亖{x|x偼俁俇偺惓偺栺悢}偲偄偆傛偆側傕偺傪峫偊傑偟傚偆丅
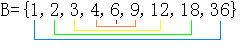
愜傝曉偡偲偙傠偱丄儁傾偑偄側偄偙偲偵婥偯偒傑偡丅
偦傟偼丄帺暘帺恎偩偐傜偱偡丅
偙偺応崌丄栺悢偺屄悢偼婏悢偲側傝傑偡偺偱丄嵟廔揑偵偼棤岦偒偵側偭偰偟傑偄傑偡丅

NO.175 丂丂丂 10/26 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮侾係乯 嵟屻傑偱偳偒偳偒偟偰偟傑偄傑偟偨偑丄偲偆偲偆傗傝傑偟偨両 偝偰丄崱夞偺擔杮僔儕亅僘偺彑偪僷僞亅儞偼丄
儀僀僗僞亅僘偺桪彑偱偡丅
崱擭偺栰媴偼丄墶昹丄墶昹丄墶昹偲偄偆傢偗偱丄壗偼偲傕偁傟偆傟偟偄偱偡偹偊丅
柧擔偺墶昹丄娭撪偁偨傝偼桪彑sale偱戝曄偐傕丒丒丒丅
乽仜仜亊亊仜仜乿偱偡丅
NO.157偺乽悈偺棳傟乿偝傫偺僨亅僞偵傛傟偽丄
夁嫀偵俁夞傕婲偙偭偰偄傞僷僞亅儞偱丄偙傟偱係夞栚偲側傝傑偡丅

NO.176 丂丂丂 10/26 丂丂悈偺棳傟 丂丂丂 捈墌拰偺栤戣乮係乯 NO.149偱採婲偟偨栤戣偱偡丅

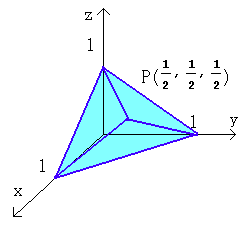
亙夝摎亜
俁偮偺暯柺偺岎揰俹偺嵗昗偼丄棫懱俲偑捈慄 x=y=z丒丒丒嘋
偵懳徧偱偁傞偙偲偵傛傝丄
嘋偲 x+y=1傪楢棫偟偰丄x=y=z=(1/2) 偱偁傞丅
偩偐傜丄棫懱俲偺戞侾徾尷偺晹暘偼塃偺恾偺傛偆偵側傞丅
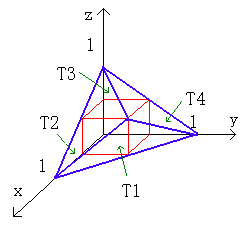
師偵丄塃偺恾偺傛偆偵丄棫懱俲偺戞侾徾尷偺晹暘傪係偮偺晹暘偵
俿1丄俿2丄俿3丄俿4偵暘妱偡傞丅
棫懱俿2丄俿3丄俿4偼丄恾宍偺懳徧惈偵傛傝丄
崌摨偱偁傞丅
棫懱俿1丄俿2偺懱愊傪偦傟偧傟
倁1丄倁2偲偡傞丅
偙偺偲偒丄棫懱俿偺懱愊傪倁偲偡傞偲丄
(倁/8)亖倁1亄俁倁2丒丒丒(仏)偱偁傞丅
俿1偼侾曈偺挿偝偑(1/2)偺棫曽懱偩偐傜丄
倁1亖(1/2)2亖(1/8)丒丒丒嘍
棫懱俿2偼丄掙柺偑侾曈偺挿偝(1/2)偺惓曽宍丄
崅偝偑(1/2)偺巐妏悕偱偁傞偐傜丄
倁2亖(1/3)亊(1/2亊1/2)亊(1/2)亖(1/24)丒丒丒嘐
廬偭偰丄媮傔傞懱愊倁偼丄嘍丄嘐傪(仏)偵戙擖偟偰丄
(倁/8)亖(1/4)傛傝丄倁亖俀丒丒丒(摎偊)
亙暿夝亜
恾宍偺懳徧惈偵傛傝丄棫懱俲偺戞侾徾尷偺晹暘偺懱愊傪俉攞偡傞偙偲偵傛偭偰丄媮傔傜傟傞丅
戞侾徾尷偵偍偄偰丄晄摍幃偼愨懳抣傪偼偢偟偰丄
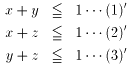
傪峫偊偰丄
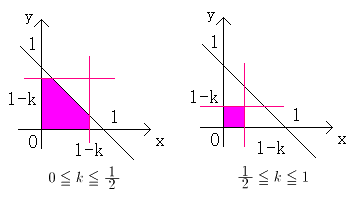 棫懱俲偺戞侾徾尷偺晹暘傪丄暯柺倸亖倠乮堦掕乯偱愗偭偨愗傝岥偼丄
塃偺恾偺幬慄晹偱偁傞丅
棫懱俲偺戞侾徾尷偺晹暘傪丄暯柺倸亖倠乮堦掕乯偱愗偭偨愗傝岥偼丄
塃偺恾偺幬慄晹偱偁傞丅


NO.177 丂丂丂 10/26 丂丂2擭4慻丂忣曬張棟壢 丂丂丂 悢棟僷僘儖(俀乯 偙傫偵偪偼丅
偙偺搙悢棟僷僘儖偺栤戣偺夝摎偵偮偄偰峫偊丄
偦偺寢壥(1)丄(2)丄(4)偺夝摎偑傢偐傝傑偟偨偺偱偙偺儊乕儖傪偍憲傝偟傑偡丅 侾丏偵偮偄偰 俀丏(1)偵偮偄偰
係俆側偳偺悢帤傪係丆俆偲偄偆傛偆偵暘夝偟偰峫偊傞丅
?偺偲偙傠偼俀丆侾偲俁丆俇傪偦傟偧傟懌偡偲侾俀偵側傞丅
姶憐
扨弮偵峫偊偰偄偨偺偱嵟弶偼偡偛偔擸傒傑偟偨丅
丂仩仩仩仩仩丂仼偙偙偵偼[41268] 枖偼[41286] 偑擖傝傑偡丅
乗丂仩仩仩仩丂仼偙偙偵偼[7935] [7953]
丂俁俁俁俁俁
係丏偵偮偄偰
[339]偲[19]傪撉傓偲乽偝傫傃傖偔偝傫偠傘偆偒傘偆乿丄
乽偠傘偆偒傘偆乿偲側傝傑偡丅
乽偝傫傃傖偔偝傫偠傘偆偒傘偆乿偐傜乽偠傘偆偒傘偆乿傪堷偔偺偱偡偐傜丄
寢壥偼乽偝傫傃傖偔偝傫乿丄偮傑傝[303]偲側傝傑偡丅

 E-mail
E-mail
 栠傞
栠傞