
Weekend Mathematics乛僐儘僉僂儉幒乛1998.7乣12乛NO.21
NO.158 丂丂丂 10/10 丂丂悈偺棳傟 丂丂丂丂悢妛偺僲乕儀儖徿乮侾乯 悽奅拞偺悢妛幰偵偲偭偰丅
傕偭偲傕傎偙傜偟偄徿偑乽僼傿乕儖僘徿乿偱偡丅
偙傟偼丄崙嵺悢妛幰夛媍偺奐夛幃偺応偵偍偄偰丄
悽奅揑偵妶桇偟偨悢妛幰偵偁偨偊傜傟傞側傜傢偟偵側偭偰偄傑偡丅
偙傟傑偱擔杮恖偱偼丄彫暯朚旻愭惗乮侾俋俆係擭庴徿乯丄
峀拞暯桽愭惗乮侾俋俈侽擭庴徿乯丄怷廳暥乮侾俋俋侽擭庴徿乯偺俁恖偑
庴徿偟偰偄傑偡丅
僲乕儀儖徿偵偼丄悢妛晹栧偑偁傝傑偣傫丅
偙傟偑丄僼傿乕儖僘徿偑乽悢妛偺僲乕儀儖徿乿偲屇偽傟傞備偊傫偱偡丅
僲乕儀儖徿偲偼堘偭偰丄僼傿乕儖僘徿偼係擭偵侾搙偟偐偁偨偊傜傟傑偣傫丅
傑偨丄僼傿乕儖僘徿偵偼乽庴徿幰偼係侽嵨枹枮偺庒偄悢妛幰偲偡傞乿
偲偄偆栺懇偑偁偭偰丄擭楊偑崅偄偲丄偄偔傜慺惏傜偟偄嬈愌傪偁偘偰傕傕傜偊傑偣傫丅
巹偑妛惗偺帪丄峀拞暯桽愭惗偑庴徿偝傟偰丄巚偄弌偑偁傝傑偡丅
堦搙偼挧愴偟偰傒傛偆偲丄扺偄柌傪帩偭偰丄妛栤偵椼傫偩婰壇偑偁傝丄
乽悢妛揑婣擺朄乿偵懳偟偰丄乽悢妛揑曎徹朄乿偲柤偮偗偰
杮傪撉傫偱丄棟榑偯偗傪偟傛偆偲尋媶偟傑偟偨丅
偦偺柌偺幚尰愭偑崱偺巹偵側偭偰偄傑偡丅丂
枹偩尒偸執戝側悢妛幰傊丄偙偺応傪棙梡偟偰丄僄乕儖傪憲傝傑偡丅
丂丂丂丂悈偺棳傟丂丂偐傜

NO.159 丂丂丂 10/11 丂丂儅僒儃乕 丂丂丂 偠傘偆偨傫偺栤戣丒偦偺屻乮俁乯 壢妛乮悢妛傪娷傔偰乯偵偲偭偰廳梫側傕偺偼丄
敪憐椡乮巚偄偮偒丄inspiration乯偲
偦傟傪徹柧偡傞偨傔偺抦幆乮抧摴側搘椡丄perspiration乯偩偲巚偄傑偡丅
僔儍乕僾巵偼帩偭偰偄傞悢妛揑抦幆偵傛傝徹柧偟傑偟偨偑丄
僞僢僋巵偼傎傏巚偄偮偒偵傛傝摎偊傪摼傑偟偨
乮偙偺巚偄偮偒偼悢妛揑偵徹柧壜擻偱偡偑丄
懡暘偁偺抜奒偱偼僞僢僋巵偼傎偲傫偳捈姶偱摎偊傪摼偨偺偱偟傚偆乯丅
壢妛幰偵偲偭偰廳梫側偙偲偼丄側偵偐暔帠傪峫偊傞偲偒偵丄
僞僢僋巵偺傛偆偵婛惉帠幚偵偲傜傢傟傞偙偲側偔
乮偄偒側傝夁嫀偺掕棟偵摉偰偼傔傞偺偱側偔乯丄
帺桼側敪憐偱傕偺偛偲傪峫偊傞偙偲偩偲巚偄傑偡丅
栜榑丄嵟廔揑偵偼徹柧偟側偗傟偽側
傝傑偣傫偐傜丄僔儍乕僾巵傛偆側棟楬惍慠側抦幆偼昁梫偱偡偑丅
巄偔偺娫僔儍乕僾巵偺峫偊偟偐晜偐偽側偐偭偨巹偵偲偭偰丄
側偐側偐捝偄偲偙傠傪撍偐傟偨栤戣偱偟偨丅

NO.160 丂丂丂 10/12 丂丂Junko 丂丂丂丂悢妛偺僲乕儀儖徿乮俀乯 僲亅儀儖徿偵偼俇偮偺庼徿晹栧
亙暥妛丄壔妛丄暔棟妛丄堛妛丒惗棟妛丄暯榓丄宱嵪妛亜偑偁傝傑偡丅
僲亅儀儖徿偵悢妛偺晹栧偑側偄偲偄偆偺偼丄抦傞恖偧抦傞榖偟偱偡丅
側偤丄悢妛偺晹栧偑側偄偐偲偄偆棟桼偵偮偄偰偼偆傢偝偑偄傠偄傠偁傞傛偆偱偡丅 僼傿亅儖僘徿偺晝丄J.C.Fields嫵庼(1863-1932,僇僫僟)偼丄
1924擭偵僇僫僟偺僩儘儞僩戝妛偵偍偄偰奐嵜偝傟偨戞俈夞崙嵺悢妛幰夛媍
傪墌妸偵塣塩偟偨偙偲偱崅偄昡壙傪庴偗偰偄傑偡丅
摉帪丄崙嵺悢妛楢崌偼戞堦師悽奅戝愴偱晧偗偨僪僀僣攈偲崙嵺悢妛楢崌攈偲
偺戝偒偔俀偮偺僌儖亅僾偵暘偐傟偰偄偰丄
崙嵺悢妛楢崌帺懱丄暘夝悺慜偺忬懺偱偟偨丅
偦傫側拞丄壗偲偐柍帠偵戞俈夞崙嵺悢妛幰夛媍傪廔椆偝偣偨棤偵偼丄
Fields嫵庼偺妶桇偑偁偭偨偺偱偡丅
敪柧壠僲亅儀儖偼悢妛偑戝偺嬯庤偱偁偭偨丄
弮悎悢妛偺壙抣偑傛偔傢偐偭偰偄側偐偭偨丄
暔棟妛偵娷傔偰峫偊偰偄偨丄
摉帪偺僗僂僃亅僨儞悢妛奅偺戝屼強Mittag-Leffler偲偺拠偑埆偐偭偨丄etc丅
杮摉偺偲偙傠偼傛偔傢偐傜側偄傛偆偱偡丅
偦偺屻丄Fields嫵庼偼昦偵搢傟傑偡偑丄偙偺帪偺帒嬥偺巆傝偺桳岠側巊偄摴傪
峫偊偰偄傑偟偨丅
偙傟偑屻偵側偭偰fields徿婎嬥偲側傝傑偡丅
傑偨丄僲亅儀儖偲摨條丄堦惗撈恎偱偡偛偟偨Fields嫵庼偵傕巕嫙偑偄傑偣傫偱偟偨丅
斵偺堚嶻傕傑偨偙偺婎嬥偵孞傝擖傟傜傟偰偄傑偡丅

NO.161 丂丂丂 10/14 丂丂悈偺棳傟 丂丂丂丂悢棟僷僘儖乮侾乯
丂丂丂
丂丂丂63丂39丂36丂28丂21
丂丂丂伀丂伀丂伀丂伀丂伀
丂45仺18仺21仺丠仺13仺7
丂
丂丂丂丂仩仩仩仩仩
丂丂丂亅丂仩仩仩仩
丂丂丂丂丳丳丳丳丳丂丂丂
丂丂丂丂俁俁俁俁俁
丂俀丆係丆俇丆俁侽丆俁俀丆俁係丆俁俇丆係侽丆係俀丆係係丆係俇丆
丂俆侽丏俆俀丆俆係丆俆俇丏俇侽丆俇俀丆俇係丆俇俇丆丠丄丠丄丒丒丒
僸儞僩丗傾儖僼傽儀僢僩偵拲堄偟傑偟傚偆丅
乽俁侽侽乿
乮偛傔傫側偝偄丄偙偺傛偆偵掶惓偟傑偡丅10/17乯
乽傛傠偟偄丅偱偼俁俁俋偐傜侾俋傪堷偔偲丠乿
乽俁俀侽乿
乽堘偄傑偡乿
乽僄僢乕乿
乽晛捠偵峫偊偰偼偄偗傑偣傫丅偝偁乕丄偄偔偮乿

NO.162 丂丂丂 10/15 丂丂Komatsu 丂丂丂丂墌偵娭偡傞旝暘乮侾俁乯 僐儘僉僂儉幒偺NO.130
傪攓尒偟傑偟偨丅
幬夞揮懱偺懱愊偺寁嶼朄偵偮偄偰偼巹偼愄丄嶲峫彂
乮搶嫗弌斉乽戝妛傊偺悢妛乿偺憹姧乽夝朄偺扵媮II乿乯
偱尒偨偙偲偑偁傝傑偡丅扐偟偦偺偲偒偼棟夝偱偒偢丄
寢嬊偦傟偭偒傝曻抲偟偰偟傑偄傑偟偨丅愭擔丄忋婰偺
倵倕倐儁乕僕傪攓尒偟丄夰偐偟偄巚偄偑偟傑偟偨丅
嵶偐偄帠偱偡偑丄忋婰倵倕倐儁乕僕偺愢柧偺拞偱
乽倁亖乧乿偺塃曈偵岆傝偑偁傝傑偡丅乽d(OP)/dx乿
偲彂偄偰偁傞偲偙傠偼丄惓偟偔偼乽d(OP)乿傑偨偼
乽(d(OP)/dx)dx乿偱偡丅
偦偺壓偺峴偺乽QP=h(x)乿偼丄惓偟偔偼乽QR=h(x)乿偱偡丅
傑偨丄偝傜偵嵶偐偄偙偲乮偲偄偆傛傝岲傒偺栤戣乯偱偡偑丄
嵟屻偵摼傜傟偨岞幃乽倁亖乧乿偺塃曈偵偁傞乽h(x)乿偼
乽f(x) - x tan兤乿偵栠偟偰偍偄偨曽偑椙偄傛偆偵巚偄傑偡丅
巹偺巜揈偺曽偑娫堘偭偰偄傞偐傕偟傟傑偣傫偑丄
壗偐偺嶲峫偵側傟偽岾偄偱偡丅

NO.163 丂丂丂 10/17 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮俇乯 NO.151
偺俀丏乽偙偺擔杮僔儕乕僘偺帋崌悢偺婜懸抣偼丠乿偲偄偆栤偵懳偡傞摎偊偲偟偰丄
NO.157偱乽悈偺棳傟乿偝傫偑夁嫀偺僨亅僞偵婎偯偄偰
俆丏俉俋俆俉俁丒丒丒偲弌偟偰偔偩偝偄傑偟偨丅 廬偭偰婜懸抣偼丄
巹偼丄墶昹儀僀僗僞亅僘偲惣晹儔僀僆儞僘偺椡偑懳摍偲壖掕偟偰寁嶼偟偰傒傑偡丅
偍屳偄偵彑偮妋棪偼(1/2)偱丄晧偗傞妋棪傕(1/2)偱偡丅
墶昹儀僀僗僞亅僘偑桪彑偡傞応崌偲惣晹儔僀僆儞僘偑桪彑偡傞応崌偲偑偁傝傑偡偐傜丄
偦傟偧傟俀攞偟傑偡丅
偙傟偼丄乽仜仜仜仜乿偟偐偁傝傑偣傫丅
侾捠傝丅
妋棪偼(1/2)4亊2=1/8
乽仩仩仩仩仜乿偲側傝傑偡丅
俆帋崌栚偼昁偢仜偱丄係偮偺仩偺拞偵俁屄偺仜偲侾屄偺亊偑擖傝傑偡丅
廬偭偰丄4俠1亖係捠傝
妋棪偼(1/2)4亊(1/2)亊4俠1亊2=1/4
乽仩仩仩仩仩仜乿偲側傝傑偡丅
俇帋崌栚偼昁偢仜偱丄俆偮偺仩偺拞偵俁屄偺仜偲俀屄偺亊偑擖傝傑偡丅
廬偭偰丄5俠2亖侾侽捠傝
妋棪偼(1/2)4亊(1/2)2亊5俠2亊2=5/16
乽仩仩仩仩仩仩仜乿偲側傝傑偡丅
俈帋崌栚偼昁偢仜偱丄俇偮偺仩偺拞偵俁屄偺仜偲俁屄偺亊偑擖傝傑偡丅
廬偭偰丄6俠3亖俀侽捠傝
妋棪偼(1/2)4亊(1/2)3亊6俠3亊2=5/16
丂4亊(1/8)亄5亊(1/4)亄6亊(5/16)亄7亊(5/16)
亖4亊(2/16)亄5亊(4/16)亄6亊(5/16)亄7亊(5/16)
亖(1/16)亊(8亄20亄30亄35)
亖(93/16)
亖5.8125
偲側傝傑偡丅
晄巚媍側偙偲偵夁嫀偺僨亅僞偲堦抳偟偰偄傑偡偹丅

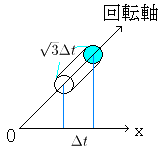
NO.164 丂丂丂 10/17 丂丂悈偺棳傟 丂丂丂丂僒僀僐儘夞揮懱乮俀乯 嵟屻偵丄彫棫懱偺岤傒偺曽岦偵懳偡傞拲堄偑昁梫偱偡丅
愗傝岥偺柺愊傪梌偊傞娭悢 倖(倲)偺曄悢倲偺曄壔検嚈倲偼丄
倶幉乮傑偨偼丄倷幉丄倸幉乯曽朄傊偺曄壔検偱偁傝丄
彫棫懱偺岤傒偺曽朄乮偙偺応崌偼夞揮幉乯偲偼堎側傞丅 偙偺栤戣偱偼丄曄悢倲偑倶幉偺惓偺曽朄偵嚈倲憹壛偡傞偲偒丄
彫棫懱偺岤傒偑幚嵺偵
夞揮幉曽朄偵偳偺偔傜偄偐傪媮傔偰傒傞偲丄
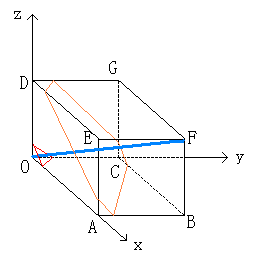
夞揮懱偺懱愊傪媮傔傞栤戣偱偡偑丄
堦斒偵夞揮懱傪夞揮幉偵悅捈側暯柺偱僗儔僀僗偡傞偲丄
偦偺愗傝岥偼墌斅丄傑偨偼丄墌娐乮僪乕僫僢僣乯偵偟偐側傜側偄偐傜丄
愗傝岥偺柺愊偼斾妑揑梕堈偵媮傔傞偙偲偑偱偒傑偡丅
偦偙偱丄偙偺栤戣偱偼丄夞揮幉俷俥忋偺揰俹傪捠傝丄
俷俥偵悅捈側暯柺兛偱
棫懱俷俙俛俠亅俢俤俥俧傪僗儔僀僗偟偨愗傝岥傪峫偊傑偡丅
偡傞偲丄暯柺兛偵傛傞棫曽懱偺愗傝岥偼丄嶰妏宍傑偨偼榋妏宍偲側傝傑偡丅
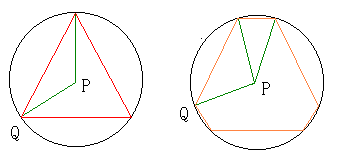
偙偙偱丄恾偺懳徧惈傪峫偊偰丄嶰妏宍傑偨偼榋妏宍偵偍偄偰丄揰俹偐傜丄
愗傝岥偺奺捀揰傊偺嫍棧偼丄偡傋偰摍偟偄丅
偙傟傜偺恾宍傪夞揮幉偺傑傢傝偱夞揮偝偣偨偲偒墌斅傪嶌傞偑丄
偦偺墌斅偺嫬奅慄傪昤偔偺偼丄夞揮偐傜嵟傕墦偄揰丄
偡側傢偪丄偙傟傜偺恾宍偺捀揰偱偁傞丅
偙偺墌斅偑丄棫懱俿偺愗傝岥偱偡丅
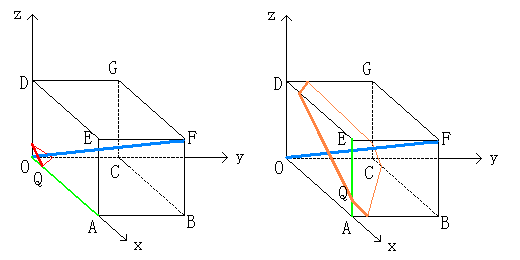
師偵丄偙偙偱摼傜傟偨墌斅偺柺愊傪揔愗側曄悢傪梡偄偰娭悢偲偟偰昞偟傑偡丅
崱弎傋偨傛偆偵丄揰俹偐傜愗傝岥偵尰傟傞惓嶰妏宍
乮傑偨偼榋妏宍乯偺奺捀揰傑偱偺嫍棧偼摍偟偄丅
備偊偵丄捀揰偺侾偮偺傪揰俻偲偡傞偲丄
揰俻偼棫曽懱俷俙俛俠亅俢俤俥俧偵偍偄偰偼丄
愜傟慄俷俙俤俥忋偵偁傞偲偟偰峫偊偰傕堦斒惈傪幐傢側偄丅
偙偺傛偆偵丄揰俹丄俻傪掕傔丄揰俹偺嵗昗傪乮倲丄倲丄倲乯丄
慄暘俹俻偺挿偝傪倖(倲)偲偡傞偲丄愗傝岥偺墌斅偺柺愊俽(倲)偼丄
俽(倲)亖兾俹俻俀亖兾{倖(倲)}俀偱梌偊傜傟傞丅


NO.165 丂丂丂 10/18 丂丂悈偺棳傟 丂丂丂 墌偵娭偡傞旝暘乮侾係乯 偛巜揈偁傝偑偲偆偛偞偄傑偟偨丅
偨偩丄h(x)=乥f(x)亅倶倲倎値兤乥偲愨懳抣傪擖傟偰偍偄偰偔偩偝偄丅

NO.166 丂丂丂 10/18 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮俈乯 偄傛偄傛擔杮僔儕亅僘偑巒傑傝傑偟偨丅
戞侾愴偼墶昹儀僀僗僞亅僘偺儅僔儞僈儞懪慄偑敋敪丄俋亅係偱彑偪傑偟偨丅
巹偼丄摿暿傋僀僗僞亅僘僼傽儞偲偄偆傢偗偱偼偁傝傑偣傫偑丄
傗偼傝抧尦僠亅儉偺妶桇偼偆傟偟偄傕偺偱偡丅 傑偢偼墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偱偡丅 廬偭偰丄墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偼丄
(1/8)+(3/16)+(3/16)+(5/32)=(21/32)偲側傝傑偡丅 師偵惣晲儔僀僆儞僘偑桪彑偡傞妋棪傪弌偟偰傒傑偡丅 廬偭偰惣晲儔僀僆儞僘偑桪彑偡傞妋棪偼丄
0+(1/16)+(1/8)+(5/32)=(11/32)偲側傝傑偡丅 師偵巆傝憤帋崌悢偺婜懸抣傪寁嶼偟偰傒傑偡丅
墶昹儀僀僗僞亅僘偑桪彑偡傞応崌偲惣晲儔僀僆儞僘偑桪彑偡傞応崌偲偑偁傝傑偡偐傜丄
偦傟偧傟偺妋棪傪懌偟偰丄帋崌悢偵偐偗偰懌偟偰偄偒傑偡丅
偝偰丄崱偺忬懺乮儀僀僗僞亅僘偑侾彑乯偱丄
偙偺屻偺妋棪傪寁嶼偟偰傒傑偟偨丅
戞俀愴埲崀丄墶昹儀僀僗僞亅僘偲惣晹儔僀僆儞僘偺椡偑懳摍偲偟偰寁嶼偟傑偡丅
偍屳偄偵彑偮妋棪偼(1/2)偱丄晧偗傞妋棪傕(1/2)偱偡丅
乽仜仜仜仜乿偟偐偁傝傑偣傫丅
妋棪偼(1/2)3=1/8
乽仜仩仩仩仜乿偲側傝傑偡丅
俆帋崌栚偼昁偢仜偱丄俁偮偺仩偺拞偵俀屄偺仜偲侾屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)3亊(1/2)亊3俠2=3/16
乽仜仩仩仩仩仜乿偲側傝傑偡丅
俇帋崌栚偼昁偢仜偱丄係偮偺仩偺拞偵俀屄偺仜偲俀屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)3亊(1/2)2亊4俠2=3/16
乽仜仩仩仩仩仩仜乿偲側傝傑偡丅
俈帋崌栚偼昁偢仜偱丄俆偮偺仩偺拞偵俀屄偺仜偲俁屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)3亊(1/2)3亊5俠2=5/32
傕偪傠傫丄(21/32)亜(1/2)偱偡丅
偁傝偊傑偣傫丅
妋棪偼0
乽亊仜仜仜仜乿偲側傝傑偡丅
妋棪偼(1/2)4=1/16
乽亊仩仩仩仩仜乿偲側傝傑偡丅
俇帋崌栚偼昁偢仜偱丄係偮偺仩偺拞偵俁屄偺仜偲侾屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)4亊(1/2)亊4俠1=1/8
乽亊仩仩仩仩仩仜乿偲側傝傑偡丅
俈帋崌栚偼昁偢仜偱丄俆偮偺仩偺拞偵俁屄偺仜偲俀屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)4亊(1/2)2亊5俠2=5/32
傕偪傠傫丄儀僀僗僞亅僘偑桪彑偡傞妋棪(21/32)偲
儔僀僆儞僘偑桪彑偡傞妋棪(11/32)傪懌偡偲1偵側傝傑偡丅
丂4亊(1/8+0)亄5亊(3/16+1/16)亄6亊(3/16+1/8)亄7亊(5/32+5/32)
亖4亊(1/8)亄5亊(1/4)亄6亊(5/16)亄7亊(5/16)
亖(1/16)亊(8亄20亄30亄35)
亖(93/16)
亖5.8125
偲側傝傑偡丅
偙傟偼丄帋崌慜偲曄傢傜側偄悢抣偱偡丅摉偨傝慜偱偡偹丅
戞侾帋崌傪徚壔偡傟偽丄昁偢偳偪傜偐偺僠亅儉偑彑偪丄
偳偪傜偐偺僠亅儉偑晧偗傑偡丅
偱傕丄巆傝帋崌悢偵偼娭學偁傝傑偣傫傕偺偹丅

NO.167 丂丂丂 10/19 丂丂Junko 丂丂丂 擔杮僔儕亅僘乮俉乯 惸摗慖庤偺戝妶桇偱傑偨傑偨儀僀僗僞亅僘偑彑偪傑偟偨丅係亅侽偱偡丅
傗偭偨亅両 墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偱偡丅 廬偭偰丄墶昹儀僀僗僞亅僘偑桪彑偡傞妋棪偼丄
(1/4)+(1/4)+(3/16)+(1/8)=(13/16)偲側傝傑偡丅 師偵惣晲儔僀僆儞僘偑桪彑偡傞妋棪傪弌偟偰傒傑偡丅 廬偭偰惣晲儔僀僆儞僘偑桪彑偡傞妋棪偼丄
0+0+(1/16)+(1/8)=(3/16)偲側傝傑偡丅 師偵憤帋崌悢偺婜懸抣傪寁嶼偟偰傒傑偡丅
墶昹儀僀僗僞亅僘偑桪彑偡傞応崌偲惣晲儔僀僆儞僘偑桪彑偡傞応崌偲偑偁傝傑偡偐傜丄
偦傟偧傟偺妋棪傪懌偟偰丄帋崌悢偵偐偗偰懌偟偰偄偒傑偡丅
壗偲尵偭偰傕俁俉擭傇傝丄墳墖偺婥崌偄偑堘偆両
偝偰丄儀僀僗僞亅僘偑俀彑偱偡丅
偙偺屻偺妋棪傪寁嶼偟偰傒傑偟偨丅
戞俀愴埲崀丄墶昹儀僀僗僞亅僘偲惣晹儔僀僆儞僘偺椡偑懳摍偲偟偰寁嶼偟傑偡丅
偍屳偄偵彑偮妋棪偼(1/2)偱丄晧偗傞妋棪傕(1/2)偱偡丅
乽仜仜仜仜乿偟偐偁傝傑偣傫丅
妋棪偼(1/2)2=1/4
乽仜仜仩仩仜乿偲側傝傑偡丅
俆帋崌栚偼昁偢仜偱丄俀偮偺仩偺拞偵侾屄偺仜偲侾屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)2亊(1/2)亊2俠1=1/4
乽仜仜仩仩仩仜乿偲側傝傑偡丅
俇帋崌栚偼昁偢仜偱丄俁偮偺仩偺拞偵侾屄偺仜偲俀屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)2亊(1/2)2亊3俠1=3/16
乽仜仜仩仩仩仩仜乿偲側傝傑偡丅
俈帋崌栚偼昁偢仜偱丄係偮偺仩偺拞偵侾屄偺仜偲俁屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)2亊(1/2)3亊4俠1=1/8
(13/16)=0.81ゥ艂穫﹤鐏A儀僀僗僞亅僘抐慠桳棙偱偡丅
偁傝偊傑偣傫丅
妋棪偼0
偁傝偊傑偣傫丅
妋棪偼0
乽亊亊仜仜仜仜乿偟偐偁傝傑偣傫丅
妋棪偼(1/2)4=1/16
乽亊亊仩仩仩仩仜乿偲側傝傑偡丅
俈帋崌栚偼昁偢仜偱丄係偮偺仩偺拞偵俁屄偺仜偲侾屄偺亊偑擖傝傑偡丅
妋棪偼(1/2)4亊(1/2)亊4俠1=1/8
傕偪傠傫丄儀僀僗僞亅僘偑桪彑偡傞妋棪(13/16)偲
儔僀僆儞僘偑桪彑偡傞妋棪(3/16)傪懌偡偲1偵側傝傑偡丅
丂4亊(1/4+0)亄5亊(1/4+0)亄6亊(3/16+1/16)亄7亊(1/8+1/8)
亖4亊(1/4)亄5亊(1/4)亄6亊(1/4)亄7亊(1/4)
亖(1/4)亊(4+5+6+7)
亖(11/2)
亖5.5
偲側傝傑偡丅
堦曽偺僠亅儉偑楢彑偡傟偽丄憤帋崌悢偺婜懸抣偼尭傞傢偗偱偡偹丅
偝偰師偼強戲媴応偱偡丅

 E-mail
E-mail
 栠傞
栠傞