
Weekend Mathematics/コロキウム室/1998.7〜12/NO.19
NO.141 9/1 Idaho Potato 世界一周
8月の「飛行機の問題 」を見て、
次のようなパズルを思い出しました。
確か、カッパブックスのパズルの本に載っていました。 「世界一周」を「地球上のすべての緯線・経線を横切ること」と定義する。
このとき、世界一周に要する移動距離の最小値は?
ただし、地球は完全な球体で、周は40000キロとする。
答えは、「20000キロ+数メートル」です。
北極点から南極点まで1本の経線に沿って移動した後に、
南極点のまわりを1周する、というわけです。

NO.142 9/1 うじちゃん くまの色
8月の「飛行機の問題 」と
「よく似た問題」です.
「熊がえさを求めて南へ2km, 東へ2km, 北へ2km歩いたら
元も場所へ戻りました.さて熊の色は何色でしょう?」
これも何かの本に載っていたものです.
「熊の色は?」というが気に入ってます.

NO.143 9/2 みかん 飛行機の問題・その後(1)
問題1(8月の「飛行機の問題 」) 問題2 問題3
地球上のある一点から、北に100キロ行き、東に100キロ行ったところから
さらに南に100キロ行ったら元に戻ったという。
どこから出発したのでしょうか?
またその場所は何ヶ所ありますか?
地球上のある一点から、北に向かって出発し100キロ行ったところで、
東に向きを変え100キロ行った。
そこからさらに進路を北にとり100キロ行ったら元に戻ったという。
どこから出発したのでしょうか?
またその場所は何ヶ所ありますか?
問題1と問題2の場所はどちらが多いですか?

NO.144 9/2 ヴァー 飛行機の問題・その後(2)
飛行機の問題についての質問があります。
「南に100キロ」というのは、経線にそって100キロ移動するわけですが、 そもそも、緯線と経線って性質の違うものですよね。 (経線の一周分の様に、球面上の円でその円周が最大の円は「大円」と呼ばれます。)
南に行くときも東に行くときもそれぞれ「大円に沿って」移動することを考えるのではないでしょうか。
間違っていたらすいませんので、どなたか返答をしてください。
「東に100キロ」というのは、緯線にそって100キロ移動するのでしょうか。
というのは、その考え方はおかしいのではないかと思っているからです。
つまり、経線はどの経線を考えてもその一周分の長さは同じです。
しかし、緯線はそうではないと思うのです。

NO.145 9/3 Idaho Potato 連続体仮説
8月の「飛行機の問題 」の解説で、
濃度に関する記述の中に、
見過ごすことのできない重大な誤りを見つけましたので、
謹んで申し上げます。 「可算濃度と連続体濃度の中間の濃度は存在しない」という命題を、
連続体仮説(Continuum Hypothesis)といい、CHと略記します。 という記述は、「CHは真である」ということと同じなので、
「誤り」と言わざるを得ません。 一般連続体仮説(GCH: Generalized Continuum Hypothesis)についても、
同様のことが証明されています。 なお、手前味噌ながら、現在、
公理的集合論ってなあに?
というページで、ZF集合論についての解説を連載していますが、
実は、この連載の最終目標が、まさしく、
「連続体仮説のZFCからの独立性」に言及することなのです。
今のところ、そこにたどり着くには、あと半年はかかりそうですが。
CHの真偽について、歴史的には次のような経緯があります。
最初に、カントールはCHは真であると信じ、証明しようと試みました。
しかし、これは成功しませんでした。
1938年、「不完全性定理」で有名なゲーデルは、
「通常の数学の範囲では、CHの否定命題を証明することはできない」
ということを証明しました。
しかし、これは、CHが真であることを意味するわけではありません。
「通常の数学」が持つ証明能力の範囲では、CHもCHの否定命題も
どちらも証明できない、という可能性があるからです。
そして、1963年にコーエンという数学者が、
「通常の数学の範囲では、CHを証明することはできない」
ということを証明しました。
したがって、CHの真偽は、
「通常の数学の範囲では、判断することができない」
という結論になるわけです。
「これを連続体問題といい、後に濃度aなる集合は存在しないことがわかっています。」
上述の「通常の数学の範囲」という言葉について、詳しく述べると、
「ツェルメロ-フレンケルの集合論の公理系」(ZFと略記される)
というものがあり、通常の数学のほとんどは、
「ZFに選択公理を付け加えた体系」(ZFCと略記される)の内部で
展開できることが知られています。
ところが、CHはZFCの証明能力を超えた命題である、というのが、
ゲーデルとコーエンによって示された結果なのです。

NO.146 9/6 ヴァー 直円柱の問題(1)
No.114の
直円柱を2つ直交させたときの共通部分の体積を求める問題の類題です。
次の図のように、半径10の直円柱を3つ直交させたときの、
この交わりの部分の体積を求めてみてください。 注:No.114の解答は、
No.131にあります。
注:図もヴァーさんの提供です。
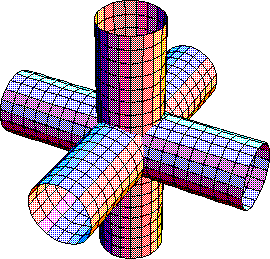

NO.147 9/7 Junko 飛行機の問題・その後(3)
飛行機の問題の中にある
「東に進む」という表現についてです。 ところが、「東に進む」というのはまたちょっと違うような気がします。 刻々と変化する中で、常に進行方向が東を向いているという風に
考えれば、それは緯線に沿って進むことになります。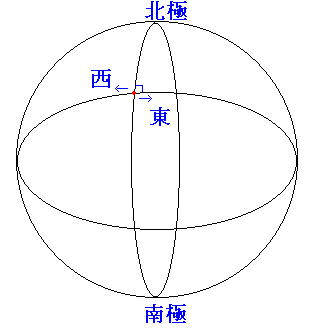
地球上で、南北というのは北極と南極の方向だということはいいかと思います。
さて、地球上のある地点での東西というのは、どういう風に決めるのでしょうか?
南北に走る経線に対して垂直な大円(一番周の長い円周)に沿って決めるのだと思います。
ですから、日本から見て東の方角はアメリカではなく、チリなのです。
(手元に地球儀があるならば、見てみてください。)
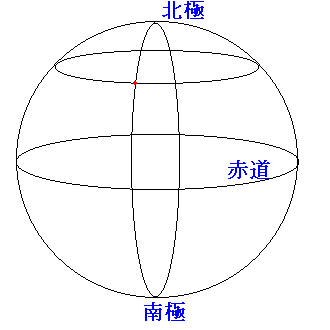
先程の大円に沿って進むと、出発した時点では確かに東を向いていたとしても、
徐々に方角が南よりになってきます。
(各場所で、経線との角度を考えてみてください。)
今回の問題はこちらの解釈でいいと思います。

NO.148 9/8 水の流れ 直円柱の問題(2)
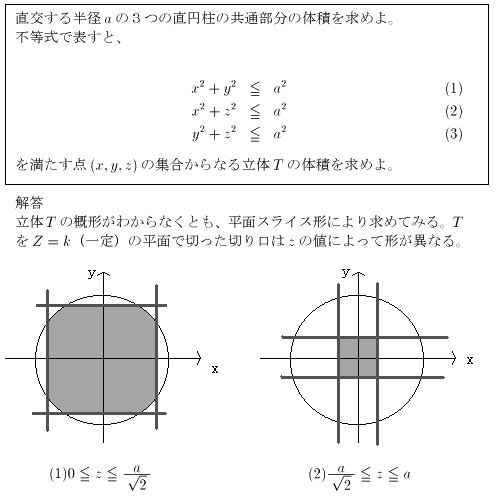



NO.149 9/8 水の流れ 直円柱の問題(3)
それでは、問題です。


 E-mail
E-mail
 戻る
戻る