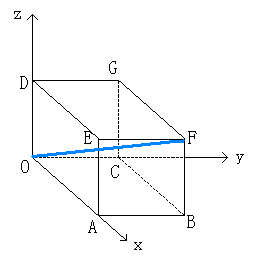
右の図のような、1辺の長さが3の立方体OABC−DEFGがある。
この立方体を、直線OFのまわりに回転して得られる立体Tの体積を求めよ。
Weekend Mathematics/コロキウム室/1998.7〜12/NO.20
NO.150 10/1 水の流れ サイコロ回転体(1)
右の図のような、1辺の長さが3の立方体OABC−DEFGがある。
この立方体を、直線OFのまわりに回転して得られる立体Tの体積を求めよ。


NO.151 10/2 水の流れ 日本シリーズ さて、横浜ベイスターズの優勝も確実になってきました。
そこで、来る日本シリーズ(先に4勝した方が優勝)に向けて、
問題です。ただし、引き分けは除外します。
たとえば、4勝3敗という場合その勝敗の順序の起こり方のことです。
○○×○××○の並び方です。
たとえば、××○○×○○となった年はないとかです。
これは、過去を調べてみれば、分かりますが、
現実に、48回も戦っていますが、あります。
どんな順序の勝敗でしょうか?
* 私は、以前に調べましたので、分かりますが。

NO.152 10/4 Idaho Potato じゅうたんの問題・その後(1) 「じゅうたんの問題」の「答えと解説」について、気になる点があります。 『求める面積は、内円に接する弦の長さにのみ依存して定まる』
という事実は、あくまで、ピタゴラスの定理を用いた議論の帰結として、
はじめて得られるものです。
その「議論」の部分を無視して、結果のみを先取りすることを、
あたかも是とするような論調には、強い抵抗を感じます。
タック社長の考え方は、数学の議論としては全く短絡的であって、
そのような考え方を「問題に対する答え」として要求するのは、
数学の問題としては、あまりに不適当ではないか、ということです。
「答えと解説」の「まとめ」には、
内側の円に外接している弦の長さだけがわかっているときに、
リングの面積を出すような公式が存在しているのだろう。
言い換えれば、弦の長さを変えなければ、
どんな半径の2つの円でもかまわないということだ。
とありますが、たぶん、タック社長がこの考えに至った理由は、
シャープ氏が「公式」の存在をほのめかしたことにあるのでしょう。
しかし、タック社長の考え方が「正しい結果を導く」ということを
主張するためには、シャープ氏のいう「公式」がいかなるもので、
さらに、それが数学的に正当であるかどうかを、
検証しなければなりません。したがって、
シャ−プさん、どうもありがとう。
でもあなたも、あなたの公式もいらないことがわかりましたよ。
というタック社長の態度は、とうてい「数学的」とはいえません。
タック社長の考えの正当性は、シャープ氏の考察があってこそ
保証されるものだからです。

NO.153 10/4 Junko じゅうたんの問題・その後(2) 確かにご指摘の通りです。
タック社長は、
「内側の円に外接している弦の長さだけで面積を求めることができる」
という仮定に基づいて考えているわけですから、
それを検証する必要はあるわけです。

NO.154 10/4 Junko 日本シリ−ズ(2) 「1.日本シリーズの勝敗の方法は何通りあるでしょう。」
を考えてみました。
先に4勝した方が勝ちで、引き分けはなしとします。
何試合で、決着したかによって分類しました。
以上のことから、1+4+10+20=35通りとなります。
これは、「○○○○」しかありません。
1通り。
「□□□□○」となります。
5試合目は必ず○で、4つの□の中に3個の○と1個の×が入ります。
従って、4C1=4通り
「□□□□□○」となります。
6試合目は必ず○で、5つの□の中に3個の○と2個の×が入ります。
従って、5C2=10通り
「□□□□□□○」となります。
7試合目は必ず○で、6つの□の中に3個の○と3個の×が入ります。
従って、6C3=20通り

NO.155 10/5 水の流れ 日本シリ−ズ(3) さて、日本シリーズの1の別解があります。
まず7回まで戦うと仮定します。
そこで、どの4つを勝つ方法は、
組み合わせ7C4=35で、あっさりでてきます。
戦っていないところは負けと考えてもよいのです。

NO.156 10/8 Junko 日本シリ−ズ(4) NO.153の
「1.日本シリーズの勝敗の方法は何通りあるでしょう。」に対する
答えとして、私が考えたNO.154と、
「水の流れ」さんがかっこよく解いた
NO.155
の別解との間には次のような等式が成り立ちます。
ところで、性質1を使うと次のような形に書き換えることができます。 更に、nCrの定義に基づいて、次のような形に変形
することもできます。
「1+4C1+5C2+6C3=7C4」
となります。
更に、先に5勝したほ方が勝ちとして、同じように式をたてると、
「1+5C1+6C2+7C3+8C4=9C5」
一般に、先にN勝した方が勝ちとすると、
「1+NC1+N+1C2+N+2C3+・・・+2N-2CN-1=2N-1CN」
これを証明します。
nCrに関する次の2つの性質を使います。
(左辺)=1+NC1+N+1C2+N+2C3+・・・+2N-2CN-1
=NC0+NC1+N+1C2+N+2C3+・・・+2N-2CN-1 (NC0=1より)
=(NC0+NC1)+N+1C2+N+2C3+・・・+2N-2CN-1
=N+1C1+N+1C2+N+2C3+・・・+2N-2CN-1 (性質2より)
=(N+1C1+N+1C2)+N+2C3+・・・+2N-2CN-1
=N+2C2+N+2C3+・・・+2N-2CN-1 (性質2より)
=(N+2C2+N+2C3)+・・・+2N-2CN-1
=N+3C3+・・・+2N-2CN-1 (性質2より)
=・・・
=(2N-2CN-2+2N-2CN-1)
=2N-1CN-1 (性質2より)
=2N-1CN (性質1より)
=(右辺)
「・・・」のところは、本来なら数学的帰納法ですかね?
(おもしろい式だと思うのですが・・・。)
先にN勝した方が勝ちとして、
「3C3+4C3+5C3+6C3=7C3」
「4C4+5C4+6C4+7C4+8C4=9C4」
「N-1CN-1+NCN-1+N+1CN-1+N+2CN-1+・・・+2N-2CN-1=2N-1CN-1」


NO.157 10/10 水の流れ 日本シリ−ズ(5) ベイスターズ優勝おめでとう。38年ぶりの悲願達成。
横浜市民は嬉しいことでしょう。 日本シリーズ勝敗の起こり方資料室 * もし7回戦を戦ったとして、何回戦の試合で4つ勝つかだから、
組み合わせの記号から、 *過去の引き分け・・・53年の第3試合、57年の第4試合、62年第3試合、
75年の第1試合と第4試合、86年の第1試合
(先に4勝した場合優勝)
C(7,4)=7×6×5÷3×2×1=35通りあります。
ただし、引き分けは除外します。
西暦で表し、下2桁で記述します。
【4回戦で終了】
1.○○○○・・・・・・ 57年西鉄(三原):巨人(水原)
<5回> 59年南海(鶴岡):巨人(水原)
60年大洋(三原):大毎(西本)
75年阪急(上田):巨人(長島)
90年西武(森) :巨人(藤田)
【5回戦で終了】
2.○○○×○・・・・・・51年巨人(水原):南海(山本)
<5回> 65年巨人(川上):南海(鶴岡)
70年巨人(川上):ロッテ(農人)
95年ヤクルト(野村):オリックス(仰木)
96年オリックス(仰木):巨人(長島)
3.○○×○○・・・・・・72年巨人(川上):阪急(西本)
<2回> 77年阪急(上田):巨人(長島)
4.○×○○○・・・・・・71年巨人(川上):阪急(西本)
<3回> 88年西武(森) :中日(星野)
97年ヤクルト(野村):西武(東尾)
5.×○○○○・・・・・・73年巨人(川上):南海(野村)
【6回戦で終了】
6.○○○××○・・・・・67年巨人(川上):阪急(西本)
7.○○×○×○・・・・・52年巨人(水原):南海(山本)
8.○○××○○・・・・・50年毎日(湯浅):松竹(小西)
<3回> 82年西武(広岡):中日(近藤)
85年阪神(吉田):西武(広岡)
9.○×○○×○・・・・・66年巨人(川上):南海(鶴岡)
<2回> 69年巨人(川上):阪急(西本)
10.○×○×○○・・・・なし
11.○××○○○・・・・なし
12.×○○○×○・・・・53年巨人(水原):南海(山本)
<4回> 56年西鉄(三原):巨人(水原)
61年巨人(川上):南海(鶴岡)
68年巨人(川上):阪急(西本)
13.×○○×○○・・・・87年西武(森):巨人(王)
<2回> 94年巨人(長島):西武(森)
14.×○×○○○・・・・74年ロッテ(金田):中日(与那嶺)
<2回> 81年巨人(藤田):日本ハム(大沢)
15.××○○○○・・・・62年東映(水原):阪神(藤本)
【7回戦で終了】
16.○○○×××○・・・76年阪急(上田):巨人(長島)
17.○○×○××○・・・93年ヤクルト(野村):西武(森)
18.○○××○×○・・・54年中日(天知):西鉄(三原)
19.○○×××○○・・・なし
20.○×○○××○・・・84年広島(古葉):阪急(上田)
21.○×○×○×○・・・なし
22.○×○××○○・・・91年西武(森):広島(山本)
23.○××○○×○・・・なし
24.○××○×○○・・・64年南海(鶴岡):阪神(藤本)
<2回> 83年西武(広岡):巨人(藤田)
25.○×××○○○・・・55年巨人(水原):南海(山本)
26.×○○○××○・・・92年西武(森):ヤクルト(野村)
27.×○○×○×○・・・63年巨人(川上):西鉄(中西)
28.×○○××○○・・・なし
29.×○×○○×○・・・78年ヤクルト(広岡):阪急(上田)
30.×○×○×○○・・・なし
31.×○××○○○・・・なし
32.××○○○×○・・・79年広島(古葉):近鉄(西本)
33.××○○×○○・・・80年広島(古葉):近鉄(西本)
34,××○×○○○・・・なし
35.×××○○○○・・・58年西鉄(三原):巨人(水原)
<3回> 86年西武(森):広島(阿南)
89年巨人(藤田):近鉄(仰木)
以上、まとめると、4回戦で終了5回、5回戦で終了11回、
6回戦で終了16回、7回戦で終了16回です。
したがって、数学的確率による試合数の期待値は
(4×5+5×11+6×16+7×16)÷48=5.89583・・・
となります。
あなたがチッケットの枚数を買うのに参考にしてください。
今年度は横浜ベイスターズと西武ライオンズとなりました。
どんな戦いになり、どんなドラマがまっているのでしょう。
私としては、過去の勝敗の起こり方にない方法で決まってほしいです。
尚、セ・パを区別すれば、2×35=70通りの決着の仕方があります。

 E-mail
E-mail
 戻る
戻る