Weekend Mathematics／コロキウム室／NO.205

コロキウム室



NO.1600 2006.6.18.K.F.連続根号数・その２(3)

（一部修正　6/20、10:00）

NO.268 連続根号数・その２(1)の問題について、 NO.549 連続根号数・その２(2) に解法が載っていますが、別解がありますので、少し長くなりますがお知らせします。

f(x)=x(x+2)･･･式１とおく。
(x+2)2=x2+4x+4
f(x+1)=(x+1)(x+3)=x2+4x+3になるから、
(x+2)2=f(x+1)+1･･･式２となる。
よって、式１，２より、

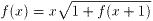　･･･式３

式３のxの代わりに、x+1を代入すると、

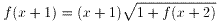　･･･式４となる。

式４を式３に代入して、

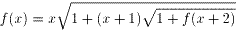　･･･式５となる。

式３のxの代わりにx+2を代入して、

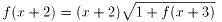　･･･式６を得る。

式６を式５に代入し、

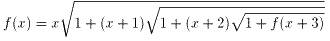　･･･式７

以下、同様に、

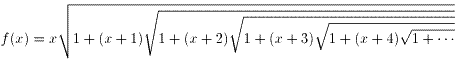　･･･式８

式８に、x=1を代入すると、

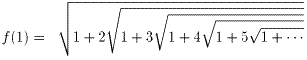　･･･式９

故に、式１より、f(1)=1･(1+2)=3



NO.1599 2006.6.18.K.F.連続根号数・その１(4)

（一部修正　6/20、10:00）

NO.267 連続根号数・その１(1)の問題について、 NO.310 連続根号数・その１(2) の解法と同じ方法で、複素数a+biの、a,bの値を求めましたが、その結果を 友人に手紙で伝えたところ、「答えは合っていると思います。 ただし、この手法では級数が収束することを証明しておかないといけないと思います。」 と指摘されました。

それから、aの値は、







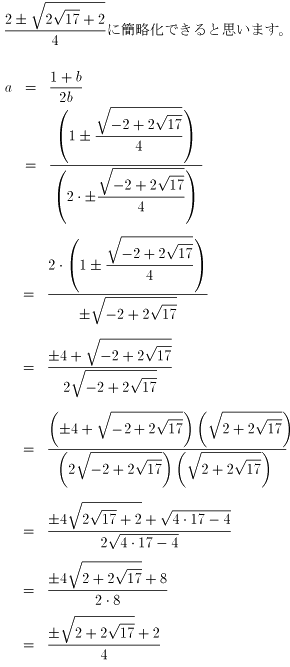
NO.1598 2006.6.12.K.F.連続根号数

下記の連続根号数について、解法または参考文献をご存知でしたら教えてください。

　　　

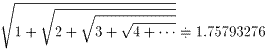
この根号数が収束することは、Ｔ・ヴィジャヤラガヴァンの定理

　　　

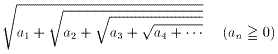
は、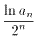の極限が存在するときに限り１つの極限に収束する。

より明らかですが、極限値が求められません。



NO.1597 2006.6.11.まこぴ〜平方数の和と差(5)

｛ｃ（ｎ，Ｐ）｝で「長さｎで値がＰとなる式」の数と定義します。 たとえば、

ｎ＝１に対して 　１＝１２　　から　ｃ（１，１）＝１、
−１＝−１２　から　ｃ（１，−１）＝１、
ｎ＝２に対して 　５＝　１２＋２２　から　ｃ（２，５）＝１、
　３＝−１２＋２２　から　ｃ（２，３）＝１、
−３＝　１２−２２　から　ｃ（２，−３）＝１、
−５＝−１２−２２　から　ｃ（２，−５）＝１、
・・・・
と続きます。特に以前の私の書き込みにより、ｃ（１９，２００６）＝１０ですね。
値Ｐを生成できないときはｃ（ｎ，Ｐ）＝０とします。
今後の議論の都合上ｃ（０，０）＝１と定義させていただきます。

実は、ｃ（ｎ，Ｐ）は次の式で計算できます。
まず初期条件：
　　ｃ（０，０）＝１
　　ｃ（０、Ｐ）＝０　（Ｐ≠０）

漸化式として：
　　ｃ（ｎ，Ｐ）＝ｃ（ｎ−１，Ｐ−ｎ２）＋ｃ（ｎ−１，Ｐ＋ｎ２）

（証明）
σ（ｉ）＝−１　ｏｒ　１とするとＰは、

　　　

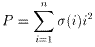
と表現できますが、

　　　

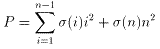
で、σ（ｎ）＝１のときは、

　　　

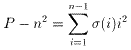
σ（ｎ）＝−１のときは、

　　　

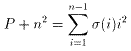
で、この２式は独立です。　（証明終わり）

実はこの漸化式でもｃ（１９，２００６）＝１０を確かめることができます。

｛ｃ（ｎ，Ｐ）｝の性質をいくつか揚げてみます。
１．ｃ（ｎ，Ｐ）＝ｃ（ｎ，−Ｐ）。
２．Ｐ＞Ｓｎ＝ｎ（ｎ＋１）（２ｎ＋１）／６ならば、ｃ（ｎ，Ｐ）＝０。
３．ｃ（ｎ，Ｓｎ）＝１。
４．
　　

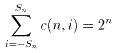
パスカルの三角形のような感じでｃ（ｎ，Ｐ）を書き出してみると 次のようになります（Ｐ≧０のみ）。

ｎ＼Ｐ０１２３４５６ ７８９1011121314・・・
０１　　　　　　 　　　　　　　　
１　１　　　　　 　　　　　　　　
２　　　１　１　 　　　　　　　　
３　　　　１　１ 　　　　　１　１

実は、具体的な表現を探査中ですが、・・・・



NO.1596 2006.6.12.水の流れリーグ戦の勝ち点表

第１７４回数学的な応募問題

皆さん、2006年ワールドカップのサッカー１次リーグの勝ち点表について興味を持っていませんか。前後半９０分の試合を行って、勝ったら勝ち点３点、引き分けたら勝ち点１点、負けたら０点となっています。ここで、３チームがリーグ戦を行った場合を考えてみます。
Ａ、Ｂ、Ｃの３チームがリーグ戦をすると、試合数は３Ｃ２＝３通り。
それぞれの試合について、一方が勝つ場合、負ける場合、引き分けの場合と３通りの勝敗が考えられるので、３３＝２７通りのケースが考えられます。それらをすべて数えてみると、勝ち点表は７通りありました。

６−３−０　・・・６通り（２勝するチームが３通り×１勝するチームが２通り）
６−１−１　・・・３通り（２勝するチームが３通り）
４−３−１　・・・６通り（１勝１引き分けのチームが３通り×１勝のチームが２通り）
４−２−１　・・・６通り（１勝１引き分けのチームが３通り×２引き分けのチームが２通り）
４−４−０　・・・３通り（１勝１引き分けが２チームで３通り）
３−３−３　・・・２通り（３すくみ状態）
２−２−２　・・・１通り（すべて引き分け）

そこで、Ａ、Ｂ、Ｃ、Ｄの４チームが１次リーグを戦います。試合数は４Ｃ２＝６通り。
それぞれの試合について、一方が勝つ場合、負ける場合、引き分けの場合と３通りの勝敗が考えられるので、６３＝７２９通りのケースが考えられます。

問題１：勝ち点表は何通りありますか。

問題２：それぞれの勝ち点表は７２９通りの中で何通りずつありますか。

注：この記事に関する投稿の掲載は、７月３日以降とします。



NO.1595 2006.6.12.ZELDA３点を通る放物線(3)

２つの接点を(s,t),(u,v)とおく。すると、(s,t)における接線は　(1/2)(y+t)=sx　である。
この直線がA(1,-2)を通るから、

　　　2s-t+2=0

同様にして、

　　　2u-v+2=0

これら２式は、(s,t),(u,v)が直線 2x-y+2=0上にあることを示している。ゆえに、B,Cを通る放物線は

　　　{(x2)-y}-k(2x-y+2)=0 と表せる。これが、A(1,-2)を通ることから、

　　　k=1/2

したがって、求める放物線の方程式は

　　　y=2(x2)-2x-2



NO.1594 2006.6.12.DDT３点を通る放物線(2)

3点を通る放物線をみつけるためには、接点の座標情報が必要です。計算過程のどこかで、判別式か微分の計算が入ってくることが予想されます。それを考えると、標準的な方法がエレガントではないかと感じました（素直なので）。さらに解答のアウトラインから考え出して、アウトラインを順次詳細化して行くうちに、いつのまにか解答に達してしまう、というやり方が、個人的にはもっともエレガントに感じます。要は、最初に、全体の見通しを立てておきます。

2次関数の一般形は、

　　　y＝bx2＋cx＋d　　　(1)

という形をしています。係数b，c，dを定めるためには、3点の座標があれば十分です。3点の座標値の代入結果は、b，c，dに関する1次方程式に過ぎないので、やれば必ず解けます。
よって、3点のうちの1つは、Ａ(1，−2) と既に与えられているので、残り2点の接点Ｂ，Ｃの座標値を具体的に求めれば OK となります。
接点を求めるには、接線情報が必要です。直線は、切片と傾きが決まれば定まりますが、接線の通過点が、Ａ(1，−2) と与えられています。つまり切片と傾きのうち、一つは既に固定されています。これを考慮して、接線を、

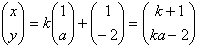　　　　　　(2)

という形に表しておきます。ここで、aは傾きです。(2)は、y軸に平行な直線を表せませんが、y軸に平行な直線が、y＝x2 に接しないのは明らかです。
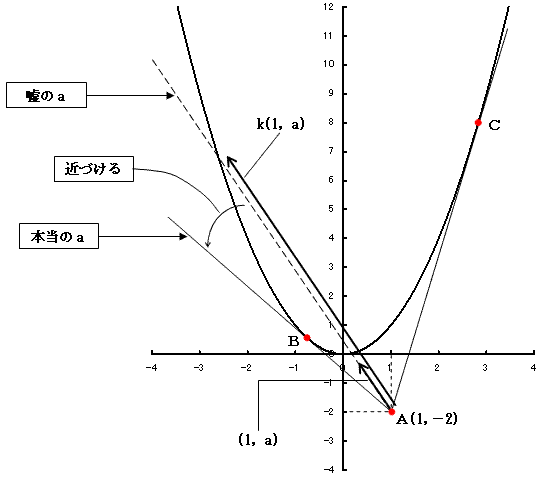
　図-1の「嘘のa」の部分を見れば明らかなように、適当なkにおいて直線(2)は、いずれにしろ 2次曲線、

　　　y＝x2　　　 (3)

と交わるはずです。kが定まれば、(2)に戻って、交点座標を計算できます。故に、全体の計算としては、kを求める手順がメインの流れです。
(2)と(3) が交わるとは、(2)の (x，y) が、(3)を満たすことです。そこで、(2)の(x，y) を (3)に代入し、

　　　ka-2=(k+1)2

をつくります。これを整理すると、 　　　k2-(a-2)k+3=0　　　(4)

が得られます。これはkの決定方程式です。ただし(4)には、未知のパラメータaが含まれています。よって、aを定める補助方程式が必要です。
図-1の「嘘のa」を「本当のa」に近づける場面を想像すれば明らかなように、「本当のa」に近づくに従って、「嘘のa」の2交点は、1点にまとまって行くので、接するとはkが重根を持つことだと、これで了解できます。kの決定方程式(4) が重根を持つとは、その判別式が0になることです。

　　　D=(a-2)2-4･1･3=0

をつくり、これを整理すれば、

　　　a2-4a-8=0　　　(5)

が得られます。これが、aに関する補助方程式です。(5)は2次方程式なので、2個のa（2本の接線）が出ます。このとき(4)を満たすkは1個のみなので、図-1の実線で表した、2本の接線に対する2個の接点（赤丸）Ｂ，Ｃが得られます。これで題意を確認できました。



方針が良さそうなので、計算を実行します。まず、(5)より、

　　　

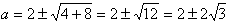
が得られます。これを(4)に代入して、

　　　

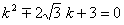
から、重根になることに注意して、

　　　

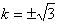
が得られます。(2)に戻って、接点座標を計算すれば、

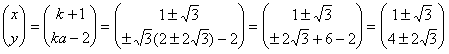　　　　　　(6)

となります。後は、これらの結果を(1)に代入して、b，c，dを定めるだけです。
(1)への代入に当たっても、(1)が、Ａ(1，−2) を通ることを考慮します。Ａ(1，−2) を通る2次関数は、

　　　y+2=b(x-1)2+c(x-1)　　　(7)

と表せるので、dに関する計算を省略できます。(7)に (6)を代入した結果は、

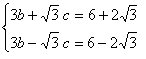　　　　　　(8)

となります。(8)の2式を、足して引いた結果は、

　　　b=c=2　　　(9)

です。(9)の結果と (7)より、求める放物線は、

　　　y=2(x-1)2+2(x-1)-2=2x2-2x-2=2(x2-x-1)

となります。



NO.1593 2006.6.11.まこぴ〜平方数の和と差(4)

（一部修正　6/12、7:00）

２００６の解が「長さ１９が最少」ということを、きちっと証明したくなりました。

　　　

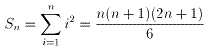
とおきます。
まず自明のこととして、

１．
長さｎの式の値の最大値は、

　　　１２＋２２＋・・・＋ｎ２＝Ｓｎ

具体的に計算してみると、

　　　Ｓ０＝０，Ｓ１＝１，Ｓ２＝５，Ｓ３＝１４，・・・

と続きます。

２．
　（１）ｎ≡０，３（ｍｏｄ　４）ならば、Ｓｎは偶数。
　（２）ｎ≡１，２（ｍｏｄ　４）ならば、Ｓｎは奇数。

（証明）
（１），（２）同時に証明します。

（１）Ｓ０＝０，Ｓ１＝１，Ｓ２＝５，Ｓ３＝１４は、主張を満たします。
（２） 　　
Ｓｎ＋４−Ｓｎ＝（ｎ＋１）２＋（ｎ＋２）２＋（ｓ＋３）２＋（ｎ＋４）２
＝４ｎ２＋２０ｎ＋３０
≡０　（ｍｏｄ　２）
よって、数学的帰納法により上の主張が正しいことが示された。　（証明終わり）

３．
　（１）ｎ≡０，３（ｍｏｄ　４）ならば、長さｎの式の値は偶数。
　（２）ｎ≡１，２（ｍｏｄ　４）ならば、長さｎの式の値は奇数。

（証明）
長さｎの式Ｐの各項について、負号「−」がついている項を｛ａ（ｋ）｝とすると、

　　　Ｐ−Ｓｎ＝−２狽＝iｋ）≡０（ｍｏｄ　２）

となるので、ＰとＳｎの偶奇は同じである。　（証明終わり）
さて、「２００６」は偶数であるので、ｎ≡０，３（ｍｏｄ　４）について考えると、

　　　Ｓ１６＝１４０８＜２００６＜Ｓ１９＝２４７０

であるので、長さ１６以下では２００６は生成できないことになります。 よって、２００６は長さ１９が最少である。



NO.1592 2006.6.4.まこぴ〜平方数の和と差(3)

（定義） １２からｎ２の和と差でできる式を、長さｎの式、あるい は、長さｎ　と言うことにしましょう。
NO.1578　tekiさんtekiさんの「長さ１９が最少」ということを、 プログラム（邪道か）で、検証できました。 ２００６に対する「長さ１９の解」は、総数で１０個あることがわかりました。 羅列しますと次のようになります。

2006= +1 +4 +9 +16 +25 -36 +49 +64 +81+100+121+144+169-196+225+256+289+324+361
2006= -1 -4 -9 +16 +25 +36 -49 +64 +81+100+121+144-169+196+225+256+289+324+361
2006= -1 -4 -9 +16 -25 +36 -49 +64 +81+100+121-144+169+196+225+256+289+324+361
2006= -1 -4 +9 +16 -25 +36 +49 +64 -81+100-121+144+169+196+225+256+289+324+361
2006= -1 -4 -9 -16 +25 +36 +49 +64 -81+100-121+144+169+196+225+256+289+324+361
2006= -1 +4 +9 +16 -25 -36 -49 +64 +81+100-121+144+169+196+225+256+289+324+361
2006= -1 +4 -9 -16 +25 -36 -49 +64 +81+100-121+144+169+196+225+256+289+324+361
2006= -1 +4 -9 -16 -25 +36 +49 +64 -81-100+121+144+169+196+225+256+289+324+361
2006= +1 -4 -9 +16 -25 +36 -49 -64 -81+100+121+144+169+196+225+256+289+324+361
2006= -1 +4 -9 -16 -25 -36 +49 -64 -81+100+121+144+169+196+225+256+289+324+361





NO.1591 2006.6.4.DDTＢ⇒(∀x)Ｂ は何故だめか？

以前からの懸案事項を考えてみたのですが、結局解決できなかったので、 またお聴きするという事態になりました。話は、初等的な命題理論と述語理論の範囲です。

一般に Ｂ ⇒ (∀x)Ｂ が何故だめかというと、これを無条件に真とすると、対偶で、 (∃x)(〜Ｂ) ⇒ 〜Ｂ も無条件に真となってしまうからです。 ここで 〜 は否定を表します。これはわかるのですが、以下に述べる状況で煮詰まっています。 ただし状況を述べる前に、論理にはいくつかの書き方があるので、使っているやり方をざっと説明したいと思います。

まず命題理論では、次の4つのシェマをとります。ouは「または」 ，⇒ は 〜ＡouＢ のことだとします。以下の Ａ，Ｂ，Ｃ は関係式です。

　　　(S1) (ＡouＡ) ⇒ Ａ
　　　(S2) Ａ ⇒ (ＡouＢ)
　　　(S3) (ＡouＢ) ⇒ (ＢouＡ)
　　　(S4) (ＡouＢ) ⇒ ((ＣouＡ) ⇒ (ＣouＢ))

ある関係式Ｂ が定理（無条件に真）であるかどうかの判定は、次の推論法則を基本とします。

Ｃ1 三段論法：
　　　Ａ と Ａ⇒Ｂ が定理なら、Ｂ は定理。

(S1)〜(S4) を、互いに代入しあったりして色々いじくりまわし、Ｃ1を必要に応じてその都度適用すると、結局次の推論法則が得られます。

Ｃ2 演繹法則（補助仮定の方法）：
Ａを仮定してＢが得られるなら、Ａ⇒Ｂ は、Ａがなくても、もともと定理である（無条件に真）。

上記法則を示すには、(S1)〜(S4) とＣ1しか使いません。この後、「かつ」を et で表わすとして、ＡetＢ を 〜((〜Ａ)ou(〜Ｂ)) のことだと定義し、Ａ⇔Ｂ を (Ａ⇒Ｂ)et(Ｂ⇒Ａ) で定義します。ここまでが命題理論です。

次は、特称と全称の限定作用素、∃と∀ です。関係式Ｒが対象を表す文字xを含んでいることを Ｒ(x) で表すことにし、τをヒルベルトのτ記号として、

　　　

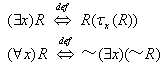
と定義します。ここで τx(Ｒ) の下付添字xは、τx(Ｒ) が、Ｒ(x) の文字xに代入されていることを示します。従って τx(Ｒ) は対象式ですが、(∃x)Ｒ を Ｒ(τx(Ｒ)) で定義するので、τx(Ｒ) は 関係式 Ｒ を満たす対象そのものです。つまり、式 τx(Ｒ) には、文字xは含まれないと考えます。
限定作用素に関するシェマとしては、

　　　(S5) Ｒ(Ｔ) ⇒ (∃x)Ｒ

をとります。ここでＴは対象式で、対象を表す任意の記号列です。もちろんＴが一文字xであってもかまいません。

命題理論から得られる結果と、(S5) を利用すると、

　　　

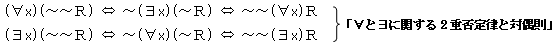
などが正当化されます。あと必要な推論法則は、次の2つです。

Ｃ3 ∀の消去：
　　　(∀x)Ｒ ⇒ Ｒ(x) は定理。

Ｃ4 ∀の追加：
Ｒ(x) が定理であり文字xが定数でないならば、(∀x)Ｒ は定理。ここで定数とは、公理に現れる文字（対象）のこと。

Ｃ3は、シェマ(S5) から直接出ます。また公理とは、ある証明を始めるにあたって最初に仮定する、条件（関係式）のことで、もちろん無条件に真です。Ｃ4を導くために、次の運用法則を認めます。

Ｃ5 代入法則：
Ｒ(x) が関係式で、定理だとする。文字xが定数でないならば、Ｔを任意の対象式として、Ｒ(Ｔ) も定理。もちろん対象式Ｔは、文字xを含まない。

証明の冒頭で、証明に固有な対象の表わし方をきちんと管理しておけば、以降では Ｒ(y) などと、Ｒ(x)をいかようにでも表して良い、というのが、Ｃ5の実際上の意味と思えます。実際これは、Ｒ(x) が無条件に正しいなら、Ｒの外延集合は普遍集合であるということと同じだと思います。Ｒ(x) は、任意の対象xで成り立つので、yやＴでも良いと。
以後、定数群はきちんと管理されていると仮定し、xが定数であるか否かには今後関わりません。そこで、Ｒ(x) が定理だとすれば、Ｃ5より Ｒ(τx(〜Ｒ)) も定理であり、

　　　Ｒ(τx(〜Ｒ)) ⇔ 〜〜Ｒ(τx(〜Ｒ)) ⇔ 〜(〜Ｒ(τx(〜Ｒ))) ⇔ 〜(∃x)(〜Ｒ) ⇔ (∀x)Ｒ

となるので、(∀x)Ｒ も定理になります。ここで使っているのは、命題理論で得られる2重否定律，(∀x)Ｒ の定義，三段論法Ｃ1です。
ここから本題に入ります。最初 Ｃ2，Ｃ3，Ｃ4を並べてみたとき、「Ｒ ⇒ (∀x)Ｒ」を導けると思いました。特にこれがあると、「Ｒ⇔Ｓ が定理なら、(∀x)Ｒ⇔(∀x)Ｓ が成り立つ」を簡単に示せます。何故ならＣ3から、「(∀x)Ｒ ⇒ Ｒ」も成り立つので、

　　　(∀x)Ｒ ⇔ Ｒ，Ｒ⇔Ｓ，Ｓ ⇔ (∀x)Ｓ

は全部定理になるので、(∀x)Ｒ または (∀x)Ｓ を仮定すれば、Ｃ1を繰り返し適用して (∀x)Ｓ または (∀x)Ｒ が定理になり、最後にＣ2を使えば、(∀x)Ｒ⇔(∀x)Ｓ が得られます。
しかし「Ｒ ⇒ (∀x)Ｒ」は最初に述べたように、いつも正しいとは限らない関係式です。「Ｒ ⇒ (∀x)Ｒ」の導出は以下のように考えていました。ただし使用している論理の書き方では、以下のような推論法則の導出のことを、「証明」と呼んではいけないことになっているのですが、ここでは読みやすくするために、［証明］と書きます。従って以下は、「間違い証明」です。

Ｃ4' ∀の追加'：
　　　Ｒ(x) ⇒ (∀x)Ｒ は定理。

［証明］
　Ｒを真と仮定する。しからばＣ5より、(∀x)Ｒ は真。Ｃ2を適用して Ｒ⇒(∀x)Ｒ は定理。

［証明終］

Ｃ4' のどこが問題かというと、演繹法則Ｃ2の適用部分です。演繹法則Ｃ2は、命題理論のシェマ(S1)〜(S4) と、三段論法Ｃ1のみを根拠としています。一方、Ｒ から (∀x)Ｒ を認める Ｃ5は、それらとは別物です。よって、Ｒを真と仮定して (∀x)Ｒを導き、Ｒ⇒(∀x)Ｒ を認めることは、演繹法則Ｃ2の適用外です。

つまり、正しいＣ4の正しさを保証するのは、じつは「Ｒを定理だとする」の一言に尽きることがわかります。

では「Ｒ⇔Ｓ が定理なら、(∀x)Ｒ⇔(∀x)Ｓ が成り立つ」を、どうやって示すかというと、⇔ の一方向が示せれば、他方も同じなので、「Ｒ⇒Ｓ が定理なら、(∀x)Ｒ⇒(∀x)Ｓ が成り立つ」を考えます。定理として使えるのは、

　　　(∀x)Ｒ ⇒ Ｒ，Ｒ⇔Ｓ

だけです。これらから、(∀x)Ｓ を導ければOKです。次のように行います。

　　　(∀x)Ｒ が真と仮定，(∀x)Ｒ ⇒ Ｒ，Ｒ⇔Ｓ

とすれば、Ｃ1を繰り返し適用することで、Ｓが真となり、Ｃ5を適用して、

　　　(∀x)Ｒ が真と仮定，(∀x)Ｒ ⇒ Ｒ，Ｒ⇔Ｓ，Ｓが真，(∀x)Ｓ が真

となり、Ｃ2を適用することで、

　　　

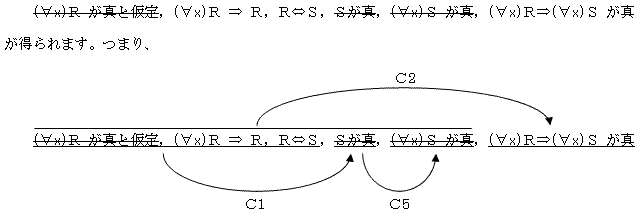
という関係になっていると思えます。

煮詰まってしまったのは、Ｃ2の適用範囲に Ｃ5が含まれることです。意味からすると、今回正しさを保証するのは、前提として与えられた「Ｒ⇔Ｓ は定理」の一言に尽き、意味からすると正しいはずです。しかし、上記関係のいったいどこが、「間違い証明 Ｃ4'」と違うのか？ が、今回お聴きしたい内容です。
恐らくふつうの書き方で言うと、「自由変数条件を満たすか否か」に関わってくると思うのですが、はっきりした対応を付けられません。
どなたか答えて頂けないでしょうか？。先日のような我儘なことは申しません。






E-mail 戻る