| NO.1580 | 2006.3.13. | 嶰妏掕婯 | 傑傢傞丂傑傢傞 |
俀侽侽俇擭俀寧偺栤戣 110亀惓曽宍偺夞揮亁傪夝偒側偑傜峫偊偨偙偲傪彂偒傑偡丅
栤戣偱偼丆廃挿3偺乪戝乫惓曽宍偺傑傢傝傪廃挿2偺乪彫乫惓曽宍偑夞揮偡傞偙偲偑僥乕儅偵側偭偰偄傑偡丅彫偼丆傕偲偺埵抲偵栠傞傑偱偵丆戝偺傑傢傝傪2.5夞揮乮900邏駬]乯偟傑偡丅
偙偺偙偲偼丆廃偺挿偝偺斾偑寛傑傟偽惓曽宍偱側偔偰傕惉傝棫偮堦斒揑側惈幙偱丆傛偔僷僘儖偵弌戣偝傟傞師偺 <栤> 偲摨偠崻偭偙偺栤戣側偺偱偡丅
<栤> 屌掕偝傟偨10墌嬍偺傑傢傝傪暿偺10墌嬍偑妸傜偢偵傕偲偺埵抲偵栠傞傑偱夞揮偡傞偲偒丆摦偔10 墌嬍偼壗夞揮偡傞偐丠
<摎> 2 夞揮 乮 仺 <恾侾>乯
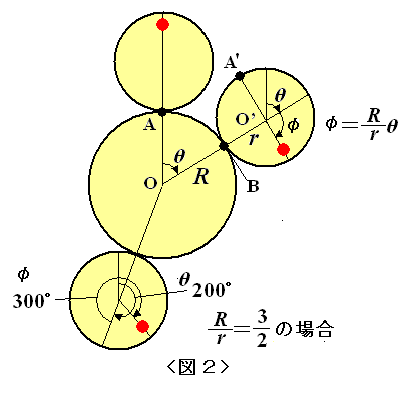
偙偺偙偲偼丆2偮偺10墌嬍偺椉曽偑丆愙揰偺埵抲傪曄偊偢偵妸傜偢偵夞揮偡傞偲偒偳偪傜傕1夞揮偡傞偙偲偐傜丆堦曽傪屌掕偡傟偽懠曽偼2夞揮偡傞偙偲偵側傞丆偲擺摼偡傞偙偲偑偱偒傑偡丅 丂偦偟偰丆偙偺偙偲偼丆2墌偺敿宎偑堎側傞応崌偵傕梕堈偵奼挘偱偒傞偺偱偡丅 丂塃 <恾俀> 偺傛偆偵丆敿宎R偺墌O偺傑傢傝傪敿宎r偺墌O乫偑妸傜偢偵夞揮偡傞偙偲傪峫偊傑偡丅2墌偺愙揰偑妏兤堏摦偟偨偲偒丆屖AB偲屖 A乫B 偼摍挿偩偐傜丆
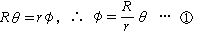
墌O乫偺夞揮妏偼丆冇亄兤 乧 嘇丅
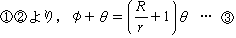
嘊偱 兤亖360亱偲偡傞偙偲偵傛傝丆
O乫偑O偺傑傢傝傪1廃偡傞偲偒
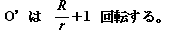
偝傜偵丆偙偺偙偲偼墌偺傒側傜偢丆擟堄偺撌恾宍偱惉傝棫偮偲巚傢傟傑偡丅
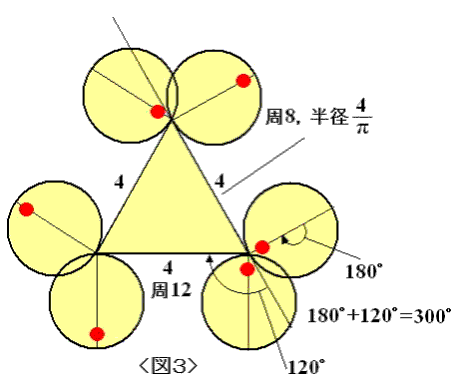
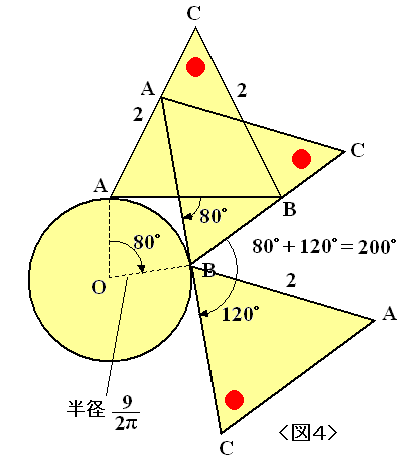
師偺 <恾俁> 偱偼丆廃12偺惓嶰妏宍偺傑傢傝傪廃8偺墌偑揮偑傝丆<恾係> 偼偦偺媡偱丆廃9偺墌偺傑傢傝傪廃6偺惓嶰妏宍偑揮偑偭偰偄傑偡丅偳偪傜偺応崌傕揮偑傞恾宍偼丆1廃偡傞拞偱2.5夞揮乮900並夞揮乯偟偰偄傑偡丅
埲忋偐傜丆師偑惉傝棫偪偦偆偱偡丅
屌掕偟偨廃L偺撌恾宍A偺傑傢傝傪廃l偺撌恾宍B偑妸傜偢偵1廃偡傞偲偒丆B偼
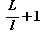 夞揮偡傞丅
偟偐偟丆巆擮側偑傜巹偵偼偙偺偙偲偺堦斒揑側徹柧偑偱偒傑偣傫丅偳側偨偐丆僄儗僈儞僩側徹柧傪梌偊偰偄偨偩偗傑偣傫偱偟傚偆偐丅
夞揮偡傞丅
偟偐偟丆巆擮側偑傜巹偵偼偙偺偙偲偺堦斒揑側徹柧偑偱偒傑偣傫丅偳側偨偐丆僄儗僈儞僩側徹柧傪梌偊偰偄偨偩偗傑偣傫偱偟傚偆偐丅

| NO.1579 | 2006.3.13. | 悈偺棳傟 | 巺偐偗 |
奆偝傫丄偙偙偵儀僯儎斅偑偁傝丄墌廃忋偵揔摉偵値杮偺揃傪懪偪傑偡丅偙偺値杮偺揃偵傕傟側偔巺偱寢傃丄偳偺巺傕岎傢傞偙偲偺側偄傛偆偵巺傪偐偗偰偄偒傑偡丅偨偩偟丄媡岦偒偵偨偳偭偰偐偗偨応崌偼摨偠偲峫偊傑偡丅
椺偊偽丄揃偑俁杮偺偲偒偼丄弴偵揃偵斣崋傪偮偗偰丄侾仺俀仺俁丂丄侾仺俁仺俀丂丄俀仺侾仺俁丂偺俁捠傝偵巺偐偗偑偱偒傑偡丅偱偼丄偙偙偱栤戣偱偡丅
栤戣侾丗値亖係偺偲偒丄壗捠傝偵側傞偐丅
栤戣俀丗値亖俆偺偲偒丄壗捠傝偵側傞偐丅
栤戣俁丗値亖俇偺偲偒丄壗捠傝偵側傞偐丅
栤戣係丗堦斒偵丄値杮偺応崌偼丄壗捠傝偵側傞偐丅
師偵丄墌廃忋偵摍娫妘偵値杮偺揃傪懪偪傑偡丅偙偺値杮偺揃偵傕傟側偔巺偱寢傃丄偳偺巺傕岎傢傞偙偲偺側偄傛偆偵巺傪偐偗偰偄偒傑偡丅偨偩偟丄媡岦偒偵偨偳偭偰偐偗偨応崌偼摨偠偲峫偊傑偡丅
偝傜偵丄儀僯儎斅傪夞揮偟偨傝丄棤曉偟偨傝偟偰摨偠宍偺巺偐偗偺応崌偼摨偠庬椶偲峫偊偰丄堎側偭偨宍偺巺偐偗偑慡晹偱壗庬椶偱偒傞偐峫偊傑偡丅椺偊偽揃偑俁杮偺偲偒偼丄侾庬椶偟偐偁傝傑偣傫丅偙偙偐傜栤戣偱偡丅
栤戣俆丗値亖係偺偲偒丄壗庬椶偵側傞偐丅
栤戣俇丗値亖俆偺偲偒丄壗庬椶偵側傞偐丅
栤戣俈丗値亖俇偺偲偒丄壗庬椶偵側傞偐丅
栤戣俉丗堦斒偵丄値杮偺応崌偼丄壗庬椶偵側傞偐丅
嶌栤偵偁偨傝僸儞僩偵側偭偨嶌昳偼
乽巺偐偗乿
偱偡丅
拲丗偙偺婰帠偵娭偡傞搳峞偺宖嵹偼丄係寧俁擔埲崀偲偟傑偡丅

| NO.1578 | 2006.3.13. | teki | 暯曽悢偺榓偲嵎(2) |
栤戣俁偩偗丄傗偭偰傒傑偟偨丅堦墳丄偱偒傑偡偹丅
| 俀侽侽俇亖 | 亅侾俀亅俀俀亅俁俀亅係俀亄俆俀亄俇俀亄俈俀亄俉俀亅俋俀亄侾侽俀亅侾侾俀亄侾俀俀亄侾俁俀亄侾係俀亄侾俆俀亄侾俇俀亄侾俈俀亄侾俉俀亄侾俋俀 |
巊偆悢帤偺屄悢偲偟偰偼丄懡暘偙傟偑嵟彮偐偲巚偄傑偡丅
栤戣侾傕峫偊偰傒傑偟偨丅
丂丂俆亖侾亄係
丂丂俇亖侾亅係亄俋
丂丂俈亖亅侾亄係亄俋亅侾俇亅俀俆亄俁俇
丂丂俉亖亅侾亅係亅俋亅侾俇亄俀俆亅俁俇亄係俋
丂丂俋亖侾亄係亄俋亅侾俇亅俀俆亄俁俇
丂侾侽亖亅侾亄係亅俋亄侾俇
栤戣俀
侾丂擟堄偺楢懕暯曽悢係偮偱係傪嶌傞偙偲偑偱偒傞丅
丂丂値俀亅乮値亄侾乯俀亅乮値亄俀乯俀亄乮値亄俁乯俀亖係
俀丂侾偐傜係傑偱偼嶌傞偙偲偑偱偒傞丅
忋婰侾丄俀傛傝慡偰偺帺慠悢傪嶌傞偙偲偑偱偒傞丅
梫偡傞偵丄侾偐傜係傑偱偑嶌傟偰丄屻偺悢偼楢懕暯曽悢係偮偱嶌偭偨係傪懌偣偽
惗惉壜擻偲偄偆偙偲偱偡丅椺偊偽
俀亖亅侾亅係亅俋亄侾俇丂偐傜丂俇亖侾亅係亅俋亄侾俇亄俀俆亅俁俇亅係俋亄俇係
俁亖亅侾亄係丂丂丂丂丂丂丂偐傜丂俈亖亅侾亄係亄俋亅侾俇亅俀俆亄俁俇
丒
丒
丒
偲偄偆嬶崌偵偱偒偰偟傑偆偲偄偆偙偲偱偡丅
偨偩偟丄偙傟偼嶌惉偑壜擻偱偁傞偲偄偆徹柧偱偁偭偰丄嵟彮屄悢偱嶌傞曽朄偵偮偄
偰偼偁傞掱搙帋峴嶖岆偑昁梫偱偡丅

 E-mail
E-mail
 栠傞
栠傞