| NO.1412 | 2003.10.22. | DDT | オイラーの座屈理論 |
１．座屈理論小史（記憶を頼りに書いたので、ちょっと嘘かも・・・）
座屈現象に最初に気づいたのは、恐らくオイラーです。オイラーとは、
古典力学の教科書を読むと必ず出てくる、あのオイラーです。
有名所では、3次元の剛体の方位を表わすオイラー角や、オイラーの独楽があります。
今風にいうと、オイラーは数学者であり（いっぱいあるオイラーの方程式！）、
物理学者であり（いっぱいあるオイラーの方程式!!）、建築家でもあり土木技術者でもありました。
（ここにさえいっぱいあるオイラーの方程式!!!）。実際、結構な数の建築物や堤防，
砂防ダムの設計に関わったそうです。以後、建築工事や土木工事の話に話題を絞りますが、
そこにはどうしても「足場」というものが出てきます。
「足場」とは、職人さん達や左官屋さんたちが壁の際にとりつき、
ペンキを塗ったりするための、まさにあの足場です。
オイラーの生きていた17世紀の頃、当時の足場は木製でした。
木柱を荒縄ロープで格子状に縦横に組み合わせ、足場が組まれました。
その構造は現在のビデ足場などと何一つ変わりません。
いまでは木製が、金属の中空鋼管（単管といわれます）になっただけです。
当時でも木材の圧縮強度がどれぐらいかは、まさに職人さん達の勘と経験によって、
おおよそは知られていました。
この強度は「木製足場に何人くらい人が乗ったら、足場は壊れるよ」という話につながります。
で、職人さん達の勘と経験によって安全だと思われる人数で足場上で作業していたら、
その足場が倒壊するという事故が度々起こりました。事故調査委員会（？）のメンバーには、
もちろんオイラーも入っていました。
柱の破壊には3つの代表的パターンがあります。圧縮破壊（圧壊）と曲げ破壊、そしてせん断破壊です。
例えばコンクリート供試体の場合、圧縮破壊においては理想的には斜め45°の破壊面が形成され、
供誌体は2つに分離します（土木や建築分野では、テストピースのことを、
試験に供する実験体という意味で、供試体と呼びます）。
この時の破壊強度は、まさに材料の圧縮強度です。
一方曲げ破壊の場合は、水平クラックがコンクリートを2つに分断し、
垂直に立てたアメの棒の頭を水平に押し続けた時のように、根元からポッキリと折れます。
この時の破壊強度は、コンクリートの引張強度によってほぼ決まり、
最後は圧縮破壊に移行したりして破壊過程はなかなか複雑なものですが、破壊面の角度などから、
圧縮破壊か曲げ破壊かは明確に区別できます。
この理由は、コンクリートは圧縮強度と引張強度とが著しく違う材料だからです。
3つ目のせん断破壊は、せん断強度によって決まるのですが、木材のせん断破壊はまずないので
（と勝手に思ってるわけですが）、ここでは省略します。
ところがオイラーも調査したであろう木材の破壊性状では、こうはいきません。
木材は、圧縮強度と引張強度がコンクリートより遥かに同等に近く、
コンクリートより遥かにたわみに強い材料です。
オイラーの見た木製足場の破壊性状は、木材がたわみに強いために、
恐らく破壊面の角度も読み取れないくらいに、のこぎり状にざくざくの状態だったか、
木材には木目があるので、それに沿って破壊面が形成されたりして圧壊か曲げ破壊かの
判定は非常に難しかったと思われます。
結局、事故調査委員会（？）のメンバーは、オイラーただ一人を除いて
「これは圧縮強度を見誤った、学のない職人どものせいだ」と判断しました。
何故なら足場の木柱は理想的には、その頭部を真っ直ぐに押す鉛直圧縮力しか受けないはずだからです。
もちろん現実的には、水平方向の力も受けますが、頭部を押す鉛直圧縮力に比べれば、
そんなものはカスに等しいはずです。この感覚は全く正しいですし、
実際に現在の計算手法で計算してみても、水平方向の力はカスです。
そして水平方向の力がカスならば、ふつう曲げ破壊は起こりません。
曲げ破壊とは、垂直に立てたアメの棒の頭を水平に押し続けた時に起こるものだからです。
しかしオイラーには、その足場の倒壊が曲げ破壊に見えました。そこでオイラーは自問しました。
「真っ直ぐに上から押されている柱にも関わらず、曲げ破壊にいたる過程は存在しないのか？」
この着想は全く正しかったことが、19世紀末に実験的に確認されます。 コンクリートという人工的な石材が開発されたのは19世紀末でした。 この人工的石材は、圧縮強度と引張強度が著しく違う材料で、 木材よりも遥かに曲げ（たわみ）に弱いものでした。 もちろんコンクリートの強度が、木材のそれを下回ると言ってるのではありません。 コンクリートは木材よりも遥かに強い材料です。ただ遥かに強い破壊強度付近に達したときに、 コンクリートは木材よりも遥かに脆いのです。そのために、
「ただ真っ直ぐに上から押されているだけにも関わらず、曲げ破壊を起こす過程の存在」
が、白日のもとに晒されました。それが座屈現象です。 オイラーは自分の理論を次のように定式化しました。
「ただ真っ直ぐに上から押されている柱が、意外なことに水平にちょっとだけ変位したら、 どのような現象が起こるだろう？」
これを、オイラーの線形座屈理論といいます。
２．初等梁理論
オイラーの線形座屈理論を説明するために、初等梁理論について、ちょっとだけ説明します。
NO.1254でも書きましたが、図-3のように一方向に著しく長い柱のようなものを梁と呼びます。
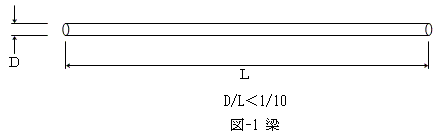
図-1の梁の厚みを表すDを梁の深さといい、梁の全長Lに比べてD/L＜1/10程度のとき、
梁ではD方向の材料の挙動は無視して良いことがわかっています。
よって梁は1次元の構造(?)です。その変形を表すには、梁の全長に沿った1個の座標xで、
じゅうぶんです。梁は曲がったり、伸びたり縮んだりします。
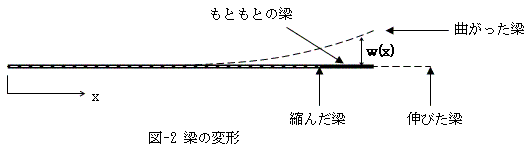
図-2の曲がった梁の各点xに対する変形量をw(x)で表わし、今回は伸び縮みの変形は考えません。
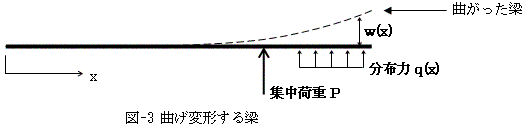
図-3において分布力はq(x)は、力の単位をN（ﾆｭｰﾄﾝ），長さの単位をm(ﾒｰﾄﾙ)とした場合、
N/mの次元を持つ力の密度であり、線荷重と言われます（まあ、圧力とでも考えて下さい）。
一方、図-3のPのように、梁の1点に作用する力そのものは、力の密度との対比で集中荷重といわれますが、
梁理論の範囲内では（本当は材料力学の範囲内であれば必ず）分布力の一種として扱われます。
すなわち集中荷重は、力の密度無限大の分布力です。
正確にはﾃﾞｨﾗｯｸのδ関数として扱うのが正当ですが、じつは結構姑息な手段でそれを分布力として扱えます。
例をあげれば、撃力を受ける質点の運動です。撃力とは無限小の時間の間に有限の運動量pを質点に与える力
のことで、撃力の力としての大きさは無限大ですが、これの初等的扱いは、質点の質量をMとした場合、
撃力の力としての大きさを問題にせず、たんに質点の初期速度p/Mを与えて運動方程式を解きます。
似たような考えに基づき、集中荷重Pを分布力として扱うとすると、結局、
梁の曲げ変形を表わす微分方程式は、式(1)のように表わせます。
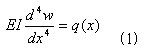
ここで係数EIは、梁の断面形状と梁を構成する材料から決まる断面定数で、1個の梁があれば、
それに対して一意に決まるものです。よって係数EIが、梁の曲げ変形性能を定義します。
また柱の全長にわたってq(x)＝0ならば、当然のことながらw(x)＝0が出ます。
「柱を横から押す力がなければ、柱は曲がらない」という至極当然の結果です。
３．オイラーの線形座屈理論
では、オイラーの座屈理論で想定された状態を図-4に書きます。オイラーは次のように考えました。
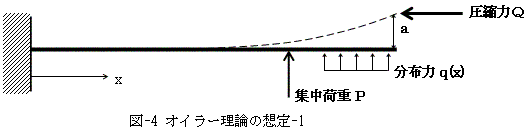
「ただ真っ直ぐに上から押されている柱が、意外なことに水平にちょっとaだけ変位したら、
どのような現象が起こるだろう？」
「真っ直ぐに上から押す力」とは図-4における圧縮力Ｑです。さらに柱は、
１．で述べたように「水平方向の力も受けますが、頭部を押す鉛直圧縮力に比べれば、
そんなものはカスに等しい」はずです。
図-4において、それはP＝0，q(x)＝0を意味します。つまりオイラーの想定した状態とは、
図-5にようなものです。
これは、はなはだ異常な事態です。aはちょっとだけなので微小なものとしますが、
柱は柱に真っ直ぐな圧縮力Ｑしか受けていないはずなのに、
柱のトップで柱直交方向にaだけ変形すると
いうのです。２．の最後で述べたように、普通に考えれば
「柱を横から押す力がなければ、柱は曲がらない」と思えます。
柱を横から押す力がないならば、柱はただ真っ直ぐに圧縮されるだけのはずです。
しかしオイラーは、図-5の状態を仮定してみました。
17世紀の足場の倒壊が、曲げ破壊に見えたからです。
図-5のように仮定したみたとして、計算結果はどうなるでしょう？。次の2つだと思われます。
(1) 柱は真っ直ぐ圧縮されるだけだ。よってオイラーは間違いだ！
(2) 柱は真っ直ぐ圧縮されるだけにも関わらず、曲げ変形を起こし、柱直交方向の力を受けたのと
同じ状態なる！
実は、どちらも正しくないのです。というか、どちらも一部だけ正しいというのが本当です。
式(1)を応用すると、図-5の状態は次の式(2)で表わせます。
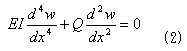
式(2)を(1)と比べると、式(1)は、
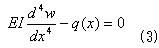
と書き直せるので、−Q･d2w/dx2が、
梁を横から押す力q(x)に相当することがわかります。
真っ直ぐに押されているだけなのに、梁は曲がると仮定したために、
こんなマッタリした項が入ってきました。
それは明らかに梁を押す力Ｑを何らかの形で含まねばなりませんが、式(2)では実際にそうなっています。
そして、
式(2)も(3)も、静力学的な力の釣り合い方程式です。このことだけは、おぼえておいて下さい。
４．オイラーの座屈方程式を解いてみる
式(2)を解いてみます。式(2)は直接2階積分できます。
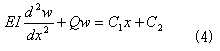
C1とC2は積分定数です。線形微分方程式(4)を解くために、(4)の特性方程式、
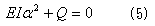
を考えます。式(5)をαに関する方程式と考えて、αについて解くと、
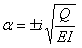
となるので（iは虚数単位）、線形微分方程式(4)の同次解は、
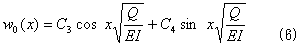
です。(4)の一般解は、(4)の同次解に特解を加えたもので、線形微分方程式の一般論に従えば、
特解は特解を生成する強制項C1x＋C2と同じ次数の多項式
w1(x)＝D1x＋D2の形を持ちます。
結局(4)の一般解は、
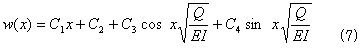
式(7)には積分定数が4つあります。解を定めるには、4つの境界条件が必要です。
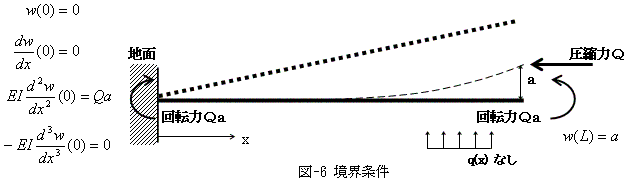
まず1つ目の条件は、柱は柱の根元x＝0で固定されているというものです。
x＝0での変形w(0)をw(0)＝0とおきます。次に柱は、柱の根元を中心とする回転にも抵抗するはずです。
柱の根元を中心とする回転に抵抗しない場合には、図-6の太点線で示したように柱は倒れ、
x＝0でも傾きdw/dxは0でないはずです。そこでこの事態を幾何学的に理想化し、
根元を中心とする回転に抵抗することを、条件(dw/dx)x=0＝0におきかえます。これが2つ目です。
残り2個の境界条件は、x＝0での力の条件です。
x＝Lで柱は、回転力Qa（偶力，ﾄﾙｸまたは力のﾓｰﾒﾝﾄと同じです）を受けています。
これは静止系なので柱に作用する外力は釣り合う必要があります。
よって柱の根元において、柱は地面から逆向きの回転力Qaを受けるはずです。
初等梁理論によれば、それはEI･(d2w/dx2)x=0に等しくなります。
従って、EI･(d2w/dx2)x=0＝Qaが3個目の条件です。4つ目は同様に、問題にしている柱は、
柱を横に押す力q(x)を持ちません。よって柱は地面から、柱直交方向の力（柱に横向きの力）を受けません。
初等梁理論でそれは −EI･(d3w/dx3)x=0＝0になります。
以上の4つの境界条件を使用するために、式(7)を順番に微分していきます。
高校生への老婆心から言うと、微分はやれば必ずできるものなので、きちんと片付けるべきです。
数学において、やれば必ずできることがわかってるなんて、めったにありません。
計算方針すら立たないのが普通です。だからいかに鉛筆が減ろうと、いかに計算が長くなろうと、
微分はきちんと片付けます（と、投稿が長くなることに言い分けしてます）。
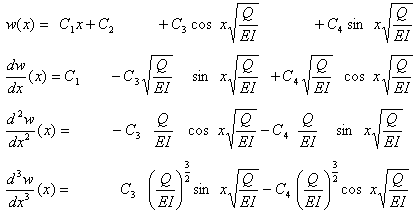
なので、
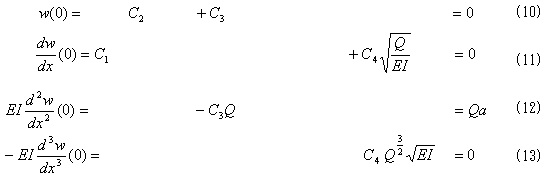
です。まず(13)よりC4＝0です。よって(11)よりC1も0。
(12)よりC3＝−aで、(10)よりC2＝a。よって問題の条件を満たす解として、
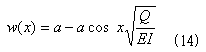
が得られます。ところが式(14)は、解が定まったという状態ではありません。
柱トップの変位aが未知のままだからです。aを定める条件はないでしょうか？。
そもそもこの話は「真っ直ぐにしか押されないはずの柱が、もし横にaだけ変位したら」
という強引な仮定のもとに始まっています。じつは、もう一つ条件があります。
「もし横にaだけ変位したら」という仮定そのものです。すなわちx＝L（柱トップ）において、
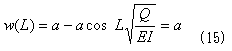
でなければなりません。これが、aを定める条件になるはずです。
ところが、式(15)の中辺のaと最右辺のaは消しあい、
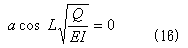
となってしまいます。普通cos部分は0ではないので、a＝0となり、
「真っ直ぐに柱を押しただけでは、柱は横には動かない（曲がらないのね、やっぱり）」という非常に納得できる結論となります。オイラーの心配は杞憂だったのでしょうか？。
５．式(16)を吟味してみる
念のため、式(16)を成立させる一般条件を調べてみます（柱は真っ直ぐ圧縮されるだけだから、
やっても無駄？）。明らかに、
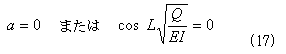
がその条件になります。a＝0が「柱は真っ直ぐ圧縮されるだけ」の状態です。
もう一つは、cosの零点を求めれば良いので、
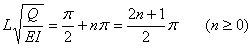
となります。Qについて解くと、
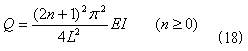
が得られます。ここでnは0以上の整数です。条件(18)が成立するとき、0でないaが可能です
（あいかわらず、その値は未知ですが）。そしてQは、柱を真っ直ぐ押す圧縮力です。
式(18)で表わされる圧縮力のことを座屈荷重といいます。以上の事態を正直に解釈すれば、
「圧縮力が座屈荷重という特定の値を持つとき柱は、純粋な圧縮力の作用下で曲がることもできる」という風に読めます。しかし「曲がることもできる」だけです。 実際、座屈荷重でないほとんど全ての圧縮力で「柱は曲がれない」のです。 それに対して、座屈荷重の作用下でさえ「柱は曲がらない」という解は可能です。 式(16)のcos部分が0であろうと、そうでなかろうと、a＝0で式(16)は成立します。 座屈荷重の作用下で、柱は本当に曲がるのでしょうか？。というか、座屈荷重という純粋な圧縮力作用下で、 柱はそもそも曲がる必要があるのでしょうか？。これらに応えるためには、静力学の中にいてはだめです。
６．純粋な静力学系など存在しない
それはこういう意味です。静力学系とは、力が釣り合った物体系のことですが、
そもそも力が瞬間的に釣り合うことはありません。例えばQ＝1Nとして、
Qが柱に作用するところをコマ撮りカメラで調べたら、瞬間的にQ＝1Nになるのではなく、
Q＝0.01N，0.1N，0.2N，0.3N・・・と、だんだんと作用する力は強くなっていくはずです。
同様に柱は、0.01mm，0.1mm，0.2mm，0.3mm・・・と、だんだんと変形するはずです
（どっち方向の変形かはおいときますが）。
コマ撮りカメラに変形が0.01mm，0.1mm，0.2mm，0.3mm・・・と写るということは、
柱は圧縮力の載荷過程で速度を持つということですし、柱の変形とQ＝1Nが瞬間的に釣り合う
というわけでもありません。全ての静力学系は、その初過程において動力学系（運動系）だということです。
ただ変形がじゅうぶん小さく載荷時間も非常に短い場合や、非常にゆっくり載荷され、
変形速度が無視できる場合には、力が瞬間的に釣り合ったとみなし、
初過程を無視して純粋な静力学系におきかえます。無視されがちですが「無限にゆっくり作用させる」
の但し書きは、このためにあります。
この立場にたてば厳密には、、座屈荷重の作用過程においても座屈荷重の載荷速度を決め、
柱の変形状態は動的な連続体力学を使って運動方程式を解くのが本当なのです。
運動方程式を解くためには、運動の初期条件が必要です。ここが重要です。つまり、
「純粋な圧縮力しか受けていない柱に、曲がる必要があるのか？」に応えるためには、まず、
「そもそも柱が曲がる必要のある初期条件は、存在するのか？」と、動力学的に問い直すべきなのです。そして余り注目されませんが、 オイラー理論の本当の価値は、この問い直しと、動的な連続体力学の運動方程式を不要に したことにあります（もちろん個人的意見ですよ）。
７．初期条件として圧縮力作用（純粋な圧縮力作用など存在しない）
純粋な圧縮力作用など存在しません。それが成り立つためには、
まず数学的に厳密に真っ直ぐな柱が必要です。次に数学的に厳密に真っ直ぐな柱に、
数学的に厳密に真っ直ぐに力を作用させる必要があります。さらに柱も力も、
まず図-7-(a)のようになるのは、真に真っ直ぐな柱は製作できないからです。
特にオイラーの時代の木柱はその典型です。現在でもmmオーダーでの製作が限度です。
図-7-(b) のようになるのは、力を作用させるにしても、作用側に別の製作物が必要だからです。
またオイラーの扱った足場では、わずかでも水平方向の力は働き、(b)と同じ状態になります。
図-7-(C) のようになるのは、どんな物体でも常に微小振動はしているからです。
オイラーの扱った足場では、職人さんたちが足場の上を歩き回ることで、
その振動が柱に伝わり(c)のような状態になったはずです。そして現在でも現実には、
近くをトラックが走れば家さえ揺れますし、風吹けば電信柱も揺れます。
図-7の(a)，(b)，(c)のいずれの圧縮力にも、柱を曲げようとする作用が伴います。
現実的に考えれば「柱が曲がる必要のある初期条件しか、そもそも存在しません」。これを、
「曲げを伴う圧縮力しか存在しない」と呼んでおきますが、では、そこらじゅうの電信柱は、図-7-(a)や(c)にように、 ぐんにゃりと曲がっているのでしょうか？。そんなことはありません。 ということは、そもそも圧縮に伴われる曲げは、通常非常に小さく無視できると結論できます。 座屈とは、伴われる微小な曲げの効果が無視できなくなった事態です。 何故そうなるのかがわかったとき、「ほとんど全ての場合の圧縮力で柱は曲がれない」と、 「圧縮力が特定の値を持つとき、柱は純粋な圧縮力の作用下で曲がることもできる」 の本当の意味がわかります。いままでのところ、これらの物理的もしくは実際的な意味合いは、 不明確なままではないでしょうか？
８．最小ポテンシャル原理
NO.1252，NO.1254でも述べたように、静力学の基本原理は全て、最小ポテンシャル原理から出てきます。
静力学の基本原理とは力の釣り合い方程式のことです。
最小ポテンシャル原理のポテンシャルとは言ってしまえば、
弾性変形エネルギーという位置ポテンシャルエネルギーのことです。
最小ポテンシャル原理とは、与えられた荷重状態に対して、
弾性変形エネルギーを最小にするように材料は変形する、という原理です。
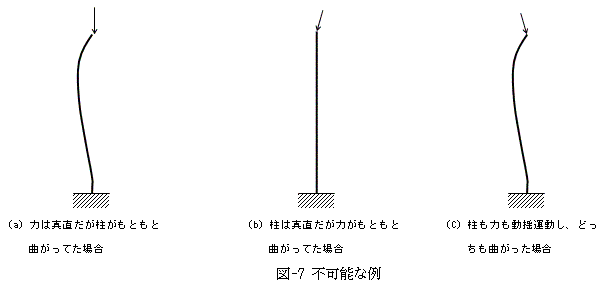
この原理は静力学系の力の釣り合い方程式を導きます。３．で式(2)が、
静力学的釣り合い方程式であることだけは、おぼえておいて欲しいと書きました。再記します。
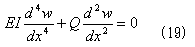
は、座屈がもし起こったと仮定した場合、力の釣り合いから式(19)を満たすように材料は変形するのですが、
このとき与えられた外力に対して、材料内部に貯まる弾性変形エネルギーは最小になります。
何故最小なのでしょう？。
弾性変形エネルギーとは、材料を微小なバネの集まりと考えた場合に、
与えられた力に抵抗するため伸びたり縮んだりしたはずの微小バネの、
そのバネエネルギーの合計です。つまり弾性変形エネルギーの大きさとは、
外力に対して材料がどれだけ無理したかを表わす指標と考えられます。
それが与えられた外力に対して最小になるように変形するとは、擬人化して言えば
「材料は楽したい」のです。材料は外力なしの無変形状態が最も楽なので、
常に無変形状態に戻りたがります。図-8に表わしたように、
これは当たり前の事実を述べたに過ぎないのですが、この擬人化は役に立ちます。
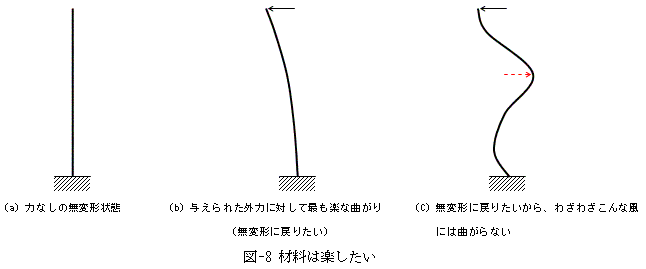
例えば図-8-(c)において、図の右向きの点線赤で書いたような力が作用しなければ、
柱トップの左向きの実線の力だけで、(c)にような変形を柱は起こすわけがありません。
柱は常に無変形状態(a)に戻りたいのです。だから、柱トップの左向きの実線の力だけが作用するなら、
(b)の状態を渋々と選択します。たとえ(c)の点線力があったとしても、
それが消失した瞬間に一気に(b)に戻るでしょう。最小ポテンシャル原理の意味とは、結局これだけです。
９．不安定釣り合いと分岐現象
５．では、純粋な圧縮力作用下で、もし柱が曲がったと仮定した場合、どんなことが起こるかを計算しました。
結論として、
1) ほとんど全ての圧縮力に対して柱は曲がれず、ただ真っ直ぐ圧縮されるだけ（納得できる！）．
というのが一つ目の結論です。しかし意外なことに、
2) 特定の圧縮力（座屈荷重）に対しては柱は曲がることも可能。でも真っ直な圧縮も、もちろん可能．
という結論にもなりました。また７．では、
3) 曲げを伴う圧縮力しか存在しない。しかし伴われる曲げは圧縮作用に比べて非常に小さい．
こともわかりました。最後に８．の結論では、
4) 力の釣り合い方程式とは、外力に対して材料が最も楽できる変形形状を決めるもの．
ということもわかりました。これらの4つの条件の全ての共通分はこうなります。
まず1)も2)も釣り合い方程式の解です。圧縮力の値が一つ決まれば、
それに対して柱は 1)か2)の状態で楽な方を選びます。
最初は 1)の状態、圧縮力が座屈荷重でない場合を考えます。
［１．座屈荷重でない場合］
1)は、純粋な圧縮力作用下で柱は曲がると仮定しても、柱は曲がれない
（a＝0）というものでしたが、4)の意味を考慮すると、
1)は、柱は曲がったら真っ直ぐ圧縮される状態より楽できないので、曲がらない、と読み直すべきです。
しかし3)より、曲げを伴う圧縮力しか存在しないのですから、柱は常に少々は曲げられているはずです。
少々というのは、やはり3)よりその曲げは、圧縮作用に比べて微小であると考えられるからです。
座屈荷重でない場合、柱は常に少々曲がっても、常にその曲げに抵抗します。
なぜなら座屈荷重でない場合には、曲がったら真っ直ぐ圧縮される状態より楽できないので、
真っ直ぐ圧縮されるだけの状態への復元力が働きます。4)より、材料は最楽状態（８．参照）
へ常に復帰したがるからです。
もちろん大きな曲げ作用が加わったら話は別です。その場合は、曲げに抵抗するより曲がってしまった方が、
材料にとって楽です。
ともあれ、圧縮力に伴う曲げ作用が圧縮力作用に比べて微小であるために、
座屈荷重でない場合には柱は、ただ真っ直ぐ圧縮されるだけのように見えます。
実際には微小な曲げが常時作用するために、復元力によって真っ直ぐ立っている位置から常に微小振動
していることになります。ところで、この動力学的結論は導くためには、動力学的な問い返しも
動的連続体力学の運動方程式も不要でした。
［２．座屈荷重の場合］
圧縮力の値が特定の座屈荷重の値をとる場合、a≠0も可能でした。
この意味は、真っ直ぐ圧縮されても曲がっても、材料にとっては同じだけ楽（もしくは同じだけ苦しい）
という意味です。よって真っ直ぐ圧縮されるだけの状態への復元力は、働きません。
ここから、3)の圧縮に伴われる微小な曲げ作用が、どこまでも拡大して行く可能性が開けます。
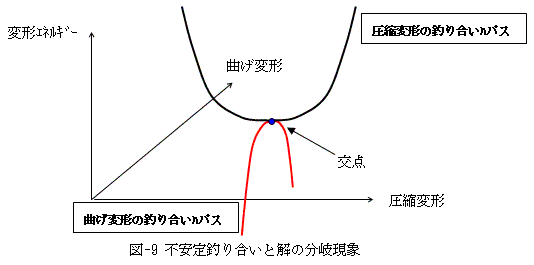
微小な曲げ作用が、どこまでも拡大して行く可能性を、図-9に示します。本当にそうなるかどうかは、
次の節で確認します（定性的になら簡単に確認できます）。
図-9では、横軸に圧縮変位，縦軸に曲げ変位，鉛直軸に弾性変形エネルギーのグラフを概念的に示します。
図-9では、圧縮変形によるエネルギー極小点が、曲げ変形によるエネルギー極大点になっています。
圧縮変形にとっても曲げ変形にとっても、その交点はエネルギーの極値となり釣り合い点なのですが、
曲げ変形にとってその点は、ちょっとした微妙な不釣合いによって、さらにエネルギーを減少させる
パスの存在する不安定釣り合い点になります。3)により、そのちょっとした微妙な不釣合いは常に存在します。
そしてその交点は、圧縮と曲げという二つの釣り合い状態を許容する点でもあります。
これを解の分岐現象といいます。
不安定釣り合い点と解の分岐が同時に存在すること、これが座屈現象の本質です。ところで、この本質を導くためには動力学的な問い返しも、動的連続体力学の運動方程式も不要です。 つまり、座屈現象は本質的に静的な過程なのです。
10．後座屈理論
ここでは９．で述べた、微小な曲げ作用がどこまでも拡大して行く過程を、定性的に追跡してみます。
図-10-(a)にように、オイラーの仮定に従って、最初に圧縮力Qに伴う微小な曲げ作用Qa0
相当の回転力が働くとします。
圧縮力に伴う回転力は微小なので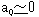
であり、
圧縮力Qはほぼ柱の真上に載っているとしてもOKです。
しかしQが座屈荷重の場合、柱は曲げ変形に抵抗しないので、
この微小な回転力によって、柱頭は有限の大きさa1だけ横に変位します。
載っている圧縮力Qは同じなので、a1だけ横に柱が変位すれば、柱には、
さらに大きな回転力Qa1が発生します。これによりさらに大きな横変位a2が発生し、
a0＜a1＜a2＜・・・とQa0＜Qa1＜Qa2＜・・・によって柱はどこまでも曲がってゆき、
最後には曲がりすぎて折れるというのが、オイラーの座屈理論の結論です。
もちろん曲がり過ぎたら、もはや線形な初等梁理論では扱えなくなりますし、
その変形は初等梁理論を応用したオイラーの線形座屈理論の適用範囲外です。
しかしオイラー理論は定性的には正しいのです。オイラー理論の後継に、後座屈理論があります。
そこでは図-10-(b)にように、柱は最初からちょっとだけ曲がっている
（曲率φの初期不整を持つと表現されます）とか、荷重はちょっとだけ傾いている
（δの偏心を持つと表現されます）とかの初期条件が必要です。
そして非線形梁理論により、図-10-(c)のような変形過程が計算され、
後座屈理論では柱の曲がり方とか、圧縮力の傾き方とかが具体的に与えられるので、
実際にどこまで横に変位するかの、変位量aも具体的に計算できます（これは密かに懸案でした）。
でもちょっと待って下さい。静的非線形計算とは、
計算過程の各ステップで材料の速度を無視するだけの準動的計算のことです。
実際その計算をスタートさせるためには、さっき言ったように初期条件が必要なのです。
オイラーの座屈理論の真の価値は、次の点にあると思えます。
オイラーは「ただ真っ直ぐに圧縮されるだけの柱が、もしちょっとでも曲がったら」
と仮定する一言のみによって、非線形計算も動的運動方程式も使わずに、
「不安定釣り合いと解の分岐現象」という本質的に静力学的な現象の、事の本質を暴き出しました。
それだけではありません。実際いまでも、座屈理論とはオイラーの線形座屈理論のことであり、
後に続いた現代的な非線形座屈理論はみな、後座屈解析（「あとざくつかいせき」と読みます）と呼ばれます。
すなわち真の座屈は、オイラーの静的線形座屈理論の範囲で起こり、その後の現象を追跡するのが、
後座屈解析の役割だというわけです。
驚くことにオイラーの座屈理論は少なくともまるごと3世紀前につくられました。
そして梁の線形初等理論をつくったのも、もちろんオイラー（とベルヌーイ）です。
これらはいまだに土木建築分野では、現役の基礎理論です。
オイラーの解析能力は、時代を超えて突出していると思えます。
| NO.1413 | 2003.10.26. | 水の流れ | 間接証明 |
先日生徒に、「間接証明として、背理法、対偶による証明、同一法があるが、
次のレームス・シュタイナー問題にチャレンジしてみなさい」
と言いました。ここで、平面幾何の問題です。もちろん、直接証明でも間接証明でも解けますからね。
三角形ＡＢＣにおいて、ＢＣ＝ａ，ＣＡ＝ｂ，ＡＢ＝ｃとする。
ＡＢ、ＡＣ上に点Ｄ、Ｅを角Ｃ，角Ｂを２等分するようにとる。
ＢＥ＝ＣＤならばＡＢ＝ＡＣ が成立することを証明せよ。
| NO.1414 | 2003.10.28. | DDT | 積分式の解 (3) |
NO.1374についてです。
理論的な解決ならNO.1381のyokodonさんの話でじゅうぶんでしょうし、
既に目的の計算も済んでいると思います（７ヶ月も経ってますよね・・・）。
なのですが、じつは私の分野でも同じ計算をやるもので、思わず筆を取ってしまいました。
それは鉄筋コンクリート構造物の塩害計算なのです。例えば海岸沿いにある鉄筋コンクリート
（堤防が際たるものです）は、海からの潮風に含まれる塩によって、鉄筋がどんどん錆びていきます。
原因は、Naclの塩素イオンcl- がコンクリートに染み込むからです。その染み込みかたといったら、
魚肉の塩分濃度と全く同じです。
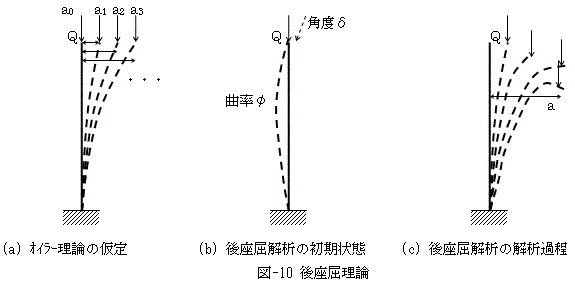
コンクリートの浸透物質の濃度分布
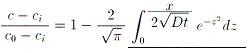
Ｃ ･･･ｺﾝｸﾘｰﾄの塩基濃度
Ｃ0 ･･･ｺﾝｸﾘｰﾄ表面濃度
Ｃi ･･･ｺﾝｸﾘｰﾄ内の初濃度
ｘ ･･･浸透面(x=0)から浸透方向にとった距離
Ｄ ･･･拡散係数
（
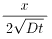・・・無次元量）
てな具合です。無次元量は鉄筋を覆うコンクリートの被り量（被り＝「かぶり」と読みます）で決まったりします。
そして、まず間違いなく最初は、exp(-x2)の積分に悩みます。
だってこんなに簡単で性質の良い関数の不定積分なんて、パッパと書けそうですもの。
でもyokodonさんが仰るようにできません。
でもexp(-x2)は非常に性質の良い関数です。概形を書けば、
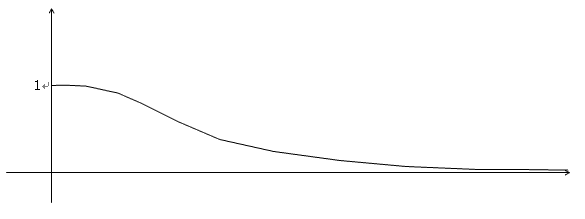
です。
台形公式でじゅうぶんじゃないですか！積分区間を100分割もすれば、実用上じゅうぶんな積分結果が得られそうです。 Excelを使いましょう。Excelはこのような繰り返し計算を最も得意とします。 Excelを使用した場合、1000〜10000分割しても結構楽々な計算が可能です。
こんなことをいうのは、級数解はx≧1において、急に収束が悪くなる場合があるからです。 yokodonさんの級数は非常に収束が良さそうですし、恐らくもう所望の計算は済んでいるのかもしれません。 ですが、このような理論も何もない計算法は、思いのほか強力だったりします。 それは関数の性質が良い場合、算法が単純なだけに誤差に強いからです。
大きなお世話でした。
| NO.1415 | 2003.10.30. | 杖のおじさん | 四捨五入、切上げ、切捨ての方法 |
一部修正 2004.9.30.
使用関数は ROUND関数（四捨五入の関数）、ROUNDUP関数、ROUNDDOWN関数、
INT関数、ABS関数（絶対値関数）を使用します。
〇 四捨五入の方法
エクセルの計算ではROUND関数（四捨五入の関数）を使用いたしますがユーザー
フォーム等VisualBasicではINT関数を使用いたします。エクセルの関数にもINT関数
はあります。
小数点以下四捨五入
例１．
１２．５６７６の場合
エクセルではROUND（１２．５６７６）＝１３
ＩＮＴ関数の場合
ＩＮＴ（１２．５６７６＋０．５）＝１３と ０．５を 加えて処理します。
１２．４７８４の場合
エクセルではROUND（１２．４７８４）＝１２
ＩＮＴ関数の場合
ＩＮＴ（１２．４７８４＋０．５）＝１２と ０．５を 加えて処理します。
小数点以下三捨四入
エクセルのROUND関数は四捨五入だけに使用するものなのでそれ以外はINT関数を使って計算致します。
例１．
１２．４２５８の場合
ＩＮＴ（１２．４２５８＋０．６）＝１３と ０．６を 加えて処理します。
１２．３１３１の場合
ＩＮＴ（１２．３１３１＋０．６）＝１２と ０．６を 加えて処理します。
〇 切上げの方法
エクセルの計算ではROUNDUP関数を使用いたしますがユーザーフォーム等VisualBasicでは
同じくINT関数を使用いたします。
数値にマイナスを付けてINT関数で処理して結果に対して（−１）を掛ける、
または結果に対してABS（絶対値関数）を使います。
例１
１０４４．２６の場合
エクセルではROUNDUP(１０４４．２６)＝１０４５
INT関数の場合は
INT(−１０４４．２６)×（−１）＝１０４５
又はABS関数（絶対値関数）を合わせて使います
ABS(INT(−１０４４．２６)）＝１０４５
〇 切捨ての方法
エクセルの計算ではROUNDDOWN関数を使用いたしますがユーザーフォーム等VisualBasicでは
同じくINT関数を使用いたします。
例１
１０４４．２６の場合
エクセルではROUNDDOWN(１０４４．２６)＝１０４４
INT関数の場合
INT (２．２３６２０６７９)＝２
それぞれの計算に於いて、小数点以下２桁で処理するときは数値を１００倍して処理し、
計算結果を１００で割ります。
INT関数の使い方はいろいろあると思いますので工夫して見て下さい。
一般的に（端数処理は）次のような計算に使います
〇 四捨五入
一般取引
土地測量、地積計算、面積計算
〇 切り上げ
電気料金計算の使用電気量
タクシー料金計算の走行距離
郵便料金計算の計量
水道料金計算の水使用量
電話の通話時間の計算
宅急便料金計算の計量
郵便貯金の利子総額が１円未満の場合は端数を切上げて１円とする。
（注）郵便貯金の利子は平成１７年４月１日より端数は切捨てとなります。
従って、０円となります。
鉄道料金計算の起点よりの距離 等
〇 切捨て
一般的なサービス産業の料金
公共料金の料金の１０円未満とか１円未満の料金
申告納税額が出る人は税金計算の納入は１００円未満、還付は円未満
消費税計算の納入は１００円未満、還付は円未満、
平成１６年４月１日より総額表示が義務付けられます。（税込価格表示）
減価償却費は円未満
以上、税金計算は税法に基づくものです
郵便貯金の利子総額が１円以上の場合は端数を切捨てとする。
手数料（証券会社、銀行）の円未満、銀行利息の円未満 等です。
（平成15年10月28日 現在の調査です）
（平成1６年 ９月29日 一部変更）
他にもあると思いますので考えて見ましょう。
地域によって料金は異なる場合がありますのでご自分で確認して見てください。自分
で計算をやると覚えます。数学の勉強が日常生活に非常に関連していることがわかり
ます。
エクセルでやって見ましょう
ABS（数値） は 数値の絶対値を返します
INT（数値） は 数値を指定した数値よりも０に近い整数に丸めた値を返します。
エクセルでは 切り上げROUNDUP,，四捨五入ROUND，切捨てROUNDDOWNの関数があります。
非常に便利な関数です。１０円未満の切捨ても、小数点３桁未満の切捨ても、何でも出来ます。
しかしユーザーフォーム等、VisualBasicのコードとしては使えません。
のでINT関数を使います。
E-mail
戻る