Weekend Mathematics/コロキウム室/NO.147
コロキウム室
| NO.1252
| 2002.8.15. | DDT | ラグラジアンの意味(1)
|
NO.1158とNO.1162
で先日ラグラジアンとハミルトニアンを紹介しましたが、
特にラグラジアンについては大問題があります。少なくとも私にとってはありました。
「ラグラジアンって何者?」「ラグラジアンの意味は何?」って難問です。
ハミルトニアンHには、力学的エネルギーEに等しいという明確な意味がありましたが、
ラグラジアンLの物理的意味は明らかに不明確です。
でもラグラジアンとハミルトニアンは良く似ています。
Tを運動エネルギー,Uを力のポテンシャルとしたとき、
ハミルトニアンHは力学的エネルギーEに等しいので、
H=T+U
となります。一方ラグラジアンLは、
L=T−U
です。私だけに限ったことではないと思いますが、
初めてラグラジアンを見た学生の多くは、力学的エネルギーEから、
何とかラグラジアンLの意味を見極めようとします。
何故なら力学的エネルギーEは、高校物理を習った過程で漠然とながらわかっているような気がし、
落体問題などを扱う場合には日常的道具だったからです。
しかしラグラジアンLには、あらかじめ言いますが物理的意味は全くありません。
それは物理的観測が不可能だとか、そういうまっとうな意味無し以上に、
本当に力学的意味を当てられない事情が存在します。
にも関わらず、ラグラジアンLは系を特徴づけます。つまり系そのものです。
ラグラジアンは最小作用の原理に関連して、その重要性が最初に見いだされます。
少なくとも力学においては、最小原理はいくつかというか多数存在します。
そもそも力学において、最小原理というものの原形はどんなものだったのでしょうか?。
話が長くなりそうなので、もうすでに題に(1)をつけてます(ずうずうしくも)。
それと地を這うような話になります。
[1].最小ポテンシャル原理
最も簡単な静力学系を考えます。バネに結合された1質点です。
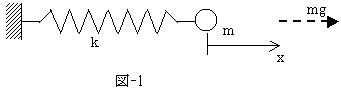
図-1に示したように、質点の質量をm,バネのバネ定数をk,mの位置を計る座標をxとします。
質点mのポテンシャルエネルギーUとは、質点mに働く力に、
わざわざマイナス符号をつけて距離で積分するものでした。
座標xの正方向は紙面右向きで、バネの力F(x)は明らかに紙面左向きの−kxなので、
mに関するポテンシャルエネルギーは、
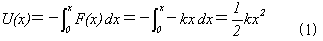
となります。でも一回くらいは、マイナスを付けないで素直にF(x)
そのものを積分したくなったことはありません
か?。もっともそのうち慣れてしまいましたが・・・。
それと「力F(x)に逆らって質点に仕事を与えるのだから、
−F(x)を積分するのだ」という取って付けたような説明は、ここで一蹴しときます。
「力F(x)に逆らって質点に仕事を与える」からこそ、与えた仕事は、
それこそF(x)そのものの積分で定義すべきだと思えるからです(← へんですか?)。
・・・それはそれとして。
(1)で定義されたポテンシャル関数U(x)の性質を調べるために、U(x)をxで微分します。
明らかに、
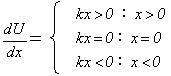 (2)
(2)
ですが、(1)よりdU/dx=−F(x)です。従って、質点mに作用するバネの力F(x)の方向は、
dU/dxで表される関数U(x)の傾きと常に符号が逆です。すなわち、
| dU/dx>0なので、F(x)<0: x>0 |
|
| dU/dx<0なので、F(x)>0: x<0 | (3)
|
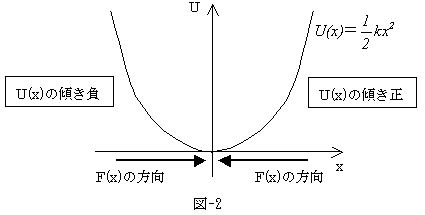 となります。それを図化したものが、図-2です。x≠0では、常にx=0へ質点を引き寄せようと
する力が働き、一方x=0は正負の傾きの変わり目なので、
dU/dx=−F(x)=0となり、質点には力が働きません。よって質点は、
x=0以外には行きたくないし、いったんx=0にはまり込んだら、そこから出てきません。
これはx=0が静力学的釣り合い点であることをいってます。
しかしこれは、図-1の質点には外力が作用しないので、
バネは伸びないままという当たり前の結論でした。
そこで図-1の質点に紙面右向きの重力mgを作用させます(点線矢印)。
ポテンシャルエネルギーは、
となります。それを図化したものが、図-2です。x≠0では、常にx=0へ質点を引き寄せようと
する力が働き、一方x=0は正負の傾きの変わり目なので、
dU/dx=−F(x)=0となり、質点には力が働きません。よって質点は、
x=0以外には行きたくないし、いったんx=0にはまり込んだら、そこから出てきません。
これはx=0が静力学的釣り合い点であることをいってます。
しかしこれは、図-1の質点には外力が作用しないので、
バネは伸びないままという当たり前の結論でした。
そこで図-1の質点に紙面右向きの重力mgを作用させます(点線矢印)。
ポテンシャルエネルギーは、
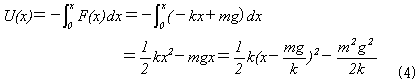
です。(4)は(1)を(mg/k,−m2g2/2k)平行移動したものなので、
今度はx=mg/k以外では、x=mg/kに押し戻そうとする力が働き、
x=mg/kではバネと重力が釣り合うという結論になります。x=mg/kはdU/dx=0の地点です。
こうなる理由は、U(x)の定義(4)そのものですが、
次の最小ポテンシャル原理が得られたことになります。
最小ポテンシャル原理
| 1. | U(x)の傾きと常に逆向きに力が働く | ←→ | dU/dx=0以外では釣り合いようがない
|
| 2. | U(x)の極小点で合力0 | ←→ | U(x)の極小点は静力学的釣り合い点
|
1.と2.は結局同じことを言ってますが、1.は2.が成り立つ理由を示しています。
しかしこの原理において、力にわざわざマイナス符号を付けて
積分することの存在理由はあるでしょうか?。
最小ポテンシャル原理によれば、ポテンシャルU(x)を微分して0とおけば、
釣り合い点もその時働く力もわかります。静力学において知りたいこととは、
およそそれらに尽きます。微分して0とおくんだから、
力にプラス符号を付けようがマイナスにしようが同じです。
実際マイナス符号を付けずにポテンシャルを定義すれば、
最大ポテンシャル原理が得られ、やっぱり微分して0とおくことになります。
マイナス符号を付けることの効果はどこに現れるのかといえば
最小ポテンシャル原理の1.の前件です。
「U(x)の傾きと常に逆向きに力が働く」ので、U(x)の「極少点が釣り合い点」です。
「U(x)の傾きと常に逆向きに力が働く」ようにしたかったといっても同じです。
いいかえれば、最小ポテンシャル原理の「最小」の二文字を得たいがために、
力にマイナス符号を付けたことになります。教科書などにはこう書かれています。
「力にマイナス符号を付けるのは、慣習による」。
「慣習による」と書かれていたとき、それはそうすることによって何かが綺麗にいくからで、
その多くは今風にいえば単に形式上の綺麗さですが、力学を造ってきた昔の人々にとっては、
譲れない哲学上の理由があったりします。昔の人々は何故「最小」にこだわったのか?。
物理学史の類書[1]などに書かれていることを圧縮して一つだけあげると、こうなります。
「宇宙は神が造った。神は完全である。だから宇宙の設計においても、
無駄は皆無の極限設計をなさったはずだ。従って物理法則は、何らかの物理量が
(エネルギーが,運動量が,時間が・・・)最小になるように定式化できる」
もちろんポテンシャルエネルギーは厳密な物理量ではありませんが、趣旨は上記の通りです。
つまり「最小性」が物理の指導原理だったのです。現在ではさすがに神はいなくても、
最小性はあいかわらず物理の指導原理の一つです。
それが証拠に、色々な変分原理であふれ返ってます。
昔の人々のこの「最小性」へのこだわりを心情的に理解できないと
、たぶんラグラジアンの成立過程には納得がいかないと思います。何故なら、
1.ラグラジアンが着想された根拠は「最小性」へのこだわり以外にはなく,
2.誰かが論理立てて導いたものでもなく,
3.数理的役割以外のラグラジアンの意味が問うことは無意味、だからです。
静力学において最小ポテンシャル原理を見つけ、最小性にこだわった昔の人々は、
当然動力学(運動現象)に対しても「運動ポテンシャル」をさがしました。
「運動ポテンシャル」は余り使われない用語ですが、実際にはある言葉で、
それはラグラジアンのことです。
[2]言い訳
最後に。1,2,3で過激なことを言いましたので、
これから述べることは全て個人的意見ですと、言い添えておきます。
[参考文献]
[1]山崎義隆,重力と力学的世界,現代数学社

| NO.1253
| 2002.8.16. | DDT | ラグラジアンの意味(2)
|
ラグラジアンの意味(1)の最後で、
1.ラグラジアンが着想された根拠は「完全無欠の神様が造った宇宙の最小性」
へのこだわり以外にはなく,
2.誰かが論理立てて導いたものでもなく,
3.数理的役割以外のラグラジアンの意味が問うことは無意味である、と書きました。
この裏の意味は、
1'その存在は前提なので、運動を決定する最小量はあれば何でも良く,
2'それに気づけば良いので誰かが導く必要もなく,
3'ラグラジアンの意味は神様がつけてくれるので問う必要はない、ということです。
しかし「1'運動を決定する最小量はあれば何でも良い」ためには、
積極的反対理由があっては駄目です。
例えば自明な制約条件からラグラジアンの形が一意に決まってしまうようであれば、
いくら最小性へのこだわりがあったところで、制約条件から決まる方を採用したはずです。
そこで力学の一般的枠組みからはラグラジアンの具体的形は決まらないことを確認するのが、
今回の目的です。
[1]力学に要請される一般的枠組み[1][2]
運動を決定するスカラー量の母関数のようなものを考え、
それをラグラジアンと呼びLで表します。Lに対する最初の条件は、
1. Lは運動を決定する.
です。運動は、各瞬間の位置と速度を全て与えれば決定するので、
L=L(v、x、t) (1)
で必要十分です。ここでtは時間,xはその時の質点の位置,vはその時のその位置での速度。ただしxやvは一般的にはベクトル量です。二つ目の条件は、
2.慣性法則.
です。ニュートンの運動法則は三つありますが、第一法則である慣性法則は別格です。
それは第二法則の運動方程式と第三法則の作用反作用の法則の成立する土台を、
第一法則が与えるからです。
力を受けない質点を自由粒子と呼びます。そうすると慣性法則は、自由粒子は等速直線運動する、
と表現できますが、この意味するところは何でしょうか?。
力とは運動状態を変えるものです。運動状態とはなんでしょうか?。
それはL=L(v,x,t)であることから(v,x,t)のことです。
時間や空間の原点を適当に選んでおけば、慣性状態においては(v,x,t)=(v,vt,t)と書けるので、
慣性状態は速度vだけで代表できます。実際運動方程式においても時間で一回積分すれば、
mv=const. (2)
です。まずラグラジアンに慣性状態を表せることを要求します。
ラグラジアンは運動方程式を与えるべきものなので、
その前提として慣性法則を表現できなければならない、という要求です。
慣性状態は速度vだけで代表できるので、自由粒子のラグラジアンは、
L0=L0(v) (3)
であるべきです(書かなかったパラメータとして質量はもちろん入るべきです。
ここでは後程考慮するといった態度で省略します)。
次に自由粒子を加速度を持った座標系から観察します。例えば発進中の飛行機の窓から。
加速度系から自由粒子を眺めたら、自由粒子といえども加速度を持ちます。
すなわち等速直線運動しません。そんなの当たり前ですが、何故当然なのでしょう?。
地上で等速直線運動する物体には、力が働いていないという確信があるからです。
ここで慣性系を定義します。物体への力の有る無しは、常に地上(地球上)では経験的に判定できる、
という確信があるために、慣性系の定義は以下のようになります。
自由粒子が等速直線運動する座標系を慣性系と呼ぶ. (4)
(4)の実質的意味はこうです。
地球は慣性系だ!.
慣性系では自由粒子は必ず等速直線運動するはずで、地球では明らかにそうだからです。
しかし(4)が地球を越えて全宇宙で普遍的に妥当するためには、
粒子が自由であるとは、慣性系において等速直線運動すること. (5)
が必要です。例えば地球から100万光年離れた地点の流星を望遠鏡で見た時に、
それが等速直線運動していたなら、自由粒子だと思いたくなります。その確信は(5)から来てます。
「慣性系だと信じている地球」から見た姿だからです。
言ってしまえば、100m先のエンジン不調のボロ車の慣性運動も、
100万光年彼方のアンドロメダ大星雲の等速直線運動も同じだと考えてるわけです。
しかも空間的距離だけでなく、100万光年彼方の100万年昔の映像を100万年後に見た時に、
同じ等速直線運動だと信じたわけですから、100秒前のも100万年前のも同じ運動だと考えてます。
これは大きな仮定です。例えば太陽系に最も近い1.5光年離れたシリウス恒星系の全ての惑星の運動は、
太陽系の惑星の運動(視認できます)と基本的に全く同じだと頭から信じてますが、
少なくとも光学望遠鏡でそれが確かめられたことはないのです
(ハップル衛星望遠鏡が見ちゃいましたっけ?)。そしてこれを、
3.時空間の一様等方性(時間や空間の性質は、場所によらず時刻によらず、どこでも同じだ!).
の仮定といいます。3.を認めた時に(4)と(5)は初めて物理的意味を持ち、
2.の慣性法則 がニュートン力学の土台を与えます。
つまり慣性法則とは、力が作用していないことの判定基準です。
その判定基準が満たされる慣性系において立てられた運動方程式に加速度が現れるなら、
本当に力が作用しているのであり、加速度系の慣性力のような見かけの力でないと判断されます。
この意味で慣性系(慣性法則が真に成り立つ座標系)は、運動方程式が成立する土台です。
論理的にはそうですが、「力の有る無しは常に経験的に判定できる」という一点に
「以上の議論は支えられている」ことを覚えておいても、損はないと思います。
ともあれ、3.は相対論的力学や標準的な量子力学にいたっても要請される非常に基本的な仮定で、
これを要求しないで済むのは、時空間の一様等方性を最初から想定しない一般相対性理論くらいです。
ところが一般相対性理論は力学理論ではなくて場の理論です。
運動方程式は消えてなくなります(つくっても良いのですが、不必要らしいのです)。
時間の一様性とはこういうことです。任意の時刻にストップウォッチのスイッチを押すことは、
運動とは無関係です。任意の時刻にストップウォッチのスイッチを押すとは、
最初に仮定していた時間軸の原点を、ストップウォッチを押した瞬間に移動することを意味します。
このような操作に、運動が無関係である以上、時間の原点移動に関してラグラジアンは不
変であるべきです(100秒前と100万年前は同じ)。
同様に空間の原点移動に対してラグラジアンが不変であれば、
それは空間の一様性の反映だとみなせます(100m先と100万光年先は同じ)。
自由粒子のラグラジアン(3)は、明らかに時空間の原点移動に対して不変です。
次に空間の等方性とは要するに、最初に仮定した空間座標をどっちの方向にふっても、
成される運動は本質的に変わらないという意味です
(JR東日本とJR東海の新幹線は、同じように走る)。例えば運動方程式、
F=ma (6)
はベクトル方程式なので、式(6)の力Fや加速度aが空間回転につられて向きを変えても、
同じ形のベクトル方程式、
F'=ma'
が得られます。この時、式(6)は空間回転に関して共変と言われます。
正確にいうと、ある操作に対して式の値が変わらないとき、
その操作に対してその式は不変といわれ、
値は変わるけれども式の形が変わらないとき共変といいます。
運動方程式は空間回転に対して共変なので、空間の等方性を反映していますが、
ラクラジアンはスカラーです。空間回転後の自由粒子のラグラジアンを成分で書き下すと
(2次元の場合)、
L0(a11v1+a12v2,
a21v1+a22v2) (7)
のようになり、もとのL0(v1,v2)とは違う関数形になります。
ここでv=(v1,v2)Tで、
a11〜a22は回転行列の成分。
自由粒子のラグラジアンL0が空間回転の影響を受けないためには、
明らかに速度ベクトルvの方向情報を含まないことです。
v自身をL0から消去するわけにはいかないので、
vの長さ|v|をv2の形で含ませます。
L0=L0(v2) (8)
式(8)の形のラグラジアンが空間回転に関して不変で、時間回転(時間軸の反転のこと)
についても不変であることは一目瞭然です。
自由粒子のラグラジアンの一般的形がこれで定まりました。
四つ目の条件は、自然のクラスター性。この条件はとても自然な経験事実です。
4.じゅうぶん遠方に離された二つの系は、相互作用しない(自然のクラスター性).
アインシュタインは、量子力学が自然のクラスター性を侵すように見えることから、
量子力学に強硬に反対しました(それとも本当に侵すのですか?。誰か教えて下さい)。
じゅうぶん遠方に離された2個の粒子を考えます。
2個の粒子は、じゅうぶん遠方に離れているので相互作用せず、
2個の自由粒子とみなせます。1個の自由粒子についてと同様な簡単な考察から、
2個の自由粒子のラグラジアンは、
L=L(v12,v22) (9)
であろうことは、すぐにわかります。
ここでLは、2個の自由粒子を含む系全体のラグラジアン
,v1とv2はそれぞれの粒子の速度です。(9)をv1で偏微分します。
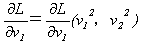 (10)
(10)
(10)の∂L/∂v1は可能性としてv1とv2を含みますが、
もし∂L/∂v1がv2を含むならば、
v1とは無関係に行えるはずのv2の変化によって、
∂L/∂v1が影響を受けることを意味します。2個の粒子は相互作用しないので、
∂L/∂v1はv1の変化のみによって決まるべきです。
よって自然のクラスター性から、∂L/∂v1はv1のみ含みます。
同様に∂L/∂v2はv2のみ含むので、
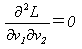 (11)
(11)
が得られます。(11)をv1とv2で積分すれば、
L=f1(v12)+f2(v22) (12)
がすぐに得られます。ここでどちらかの粒子がなかった場合を考えれば明らかなように、
f1とf2はそれぞれの自由粒子のラグラジアンに等しく、
1個の自由粒子のラグラジアン(6)と同じ形であるべきです。
すなわち2個の自由粒子のラグラジアンの和として書けるべきです。
L=L0(v12)+L0(v22) (13)
このような性質をラグラジアンの加法性といい、
自然のクラスター性から導かれる経験的事実です。
次に2個の粒子を近づけて相互作用させます。
そのときのラグラジアンをL12(v1,v2,x1,x2,t)として、
差φ12、
L12(v1,v2,x1,x2,t)
−L0(v12)−L0(v22)=
φ12(v1,v2,x1,x2,t) (14)
は、自由状態からの2粒子のずれ、相互作用項であるはずです。
x1とx2は2粒子の位置を表し、φ12に速度や時間が現れるのは、
速度に依存する相互作用であったり、時間に関して脈動するような相互作用かもしれないからです。
ここで古典力学の特殊事情を使います。
5.古典力学では現象論的な力の伝達を除いて、
素過程の力の伝達は全て相対位置のみで決まる.
言うまでもなく、これの代表例はニュートンの万有引力の法則です。
5.を認めると式(14)より、2個の質点のラグラジアンは一般的に、
L12(v1,v2,x1,x2,t)
=L0(v12)+L0(v22)=
φ12(x12) (15)
という形を持ちます。ここでx12=x2−x1であり、
φ12はx12の偶関数であるべきです。
作用反作用の法則より、φ12は、x1,x2について極性(方向性)
を持ってはいけないからです。式(14)を導いたのと同様な考察を、
n質点系に繰り返し用いると、結局、
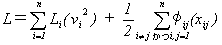 (16)
(16)
が得られます。式(16)の第2項に係数1/2を付けるは、全ての(i,j)について和をとると
φijを2回づつ勘定することになるためで、
とjを平等に扱いたいという願いから生じた、趣味もしくは慣習です
(ただし微分形式や交代化演算を考慮すると、この形が便利です)。
式(16)まで来ると、普通のラグラジアンまで後一歩という印象を受けます。
しかしこの辺りが限度です。それは次のガリレイ変換を試みるとすぐわかります。
[2]ガリレイの相対性原理とラグラジアンの不定性[1][3]
さっきニュートンの第一法則(慣性則)は、他の法則と比べて別格だと書きましたが、
これを認めると、ガリレイの相対性原理は避けて通れなくなります。
ガリレイの相対性原理は、互いに等速直線運動する二つの慣性系間の時間を含めた
座標変換を与えますが、これによって運動方程式は少なくとも共変でなければなりません。
そうでなければ全ての慣性系が同等にならないからです。
これは、3の時空間の一様等方性からの直接の要求です。
3が、いかなる場所のいかなる時刻の慣性系で運動を調べようと同じだと、
せっかく保証してくれてるのに、運動を記述する運動方程式の方が、
慣性系間の座標変換で変化してしまっては、お話になりません。
実際運動方程式は、5.古典力学の特殊事情を認める限り、ガリレイ変換で不変です。
運動を調べる2つの座標系(x,t)と(x',t')系があり、
(x,t)系と(x',t')系が互いに相対的に等速直線運動しているとき、ガリレイ変換は、
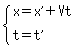 (17)
(17)
と書けます。x,x',Vはベクトルで、Vが2つの座標系間の等速な相対速度を表します。
要するにガリレイ変換で運動方程式が不変(または共変)とは、一定速度で走るバスがあって、
それより半端じゃなく速いがやはり一定速度のバスがすれ違ったとき、
最初のバス内で野球をやってた少年少女達と全く同一なコピーが、後のバスにいたとして、
全く同じ野球をやってるか?という話です。常識的に考えればできるに決まってます。
それを理論上正当化するのが、ガリレイ変換での運動方程式の不変(または共変性)です。
(15)にならって(16)を書き直すと、
L=L0(v2)+φ(x) (18)
と書けますが、式(18)のxは、式(16)の相対座標の集まりを表します。
従って、運動を観測する座標系が(x,t)から(x',t')に移っても、
φ(x)には変化はありません。問題は式(18)のL0(v2)のほうです。
式(17)によれば、変換後の式(16)のvはv'+Vに変化します。
それは式(17)の第1式をtで微分すれば、すぐわかります。変換後のL0の姿は、
L0((v'+V)2)=
L0(v'2+2v'V+V2)
≠L0(v'2) (19)
となり、L0(v)は変換v → v' について共変ではありません。
原因は明らかに相対速度Vです。ところが式(19)が相対速度Vの影響を受けないと仮定すると、
式(19)は(v'+V)を含めないという結論になってしまいます。
ここにいたってラグラジアンは不可能になるのでしょうか?。
しかしことはそう簡単ではありません。
今までラグラジアンに対して色々な制限を加えてきましたが、
最終的には正しい運動方程式が得られれば、それで良いのです。
そうすると、ラグラジアンから運動方程式を導く変換方法も問題になってきます。
この立場で行くと、ラグラジアンが1.で行ったような種々の制限を満たすのであれば、
変換後の運動方程式にもそれらの制限は反映されるのでそれはそれで良く、
必ずしもラグラジアンが力学に要請される全ての一般的制約を、
全部満たさなくても良いことになります。
じつはラグラジアンから運動方程式が、
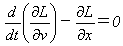 (20)
(20)
で得られることさえ認めてしまえば、同一の運動方程式を導くラグラジアンの形は無数にあります。
その中でも最も一般的で普遍的な不定性は、
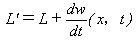 (21)
(21)
の形のものです。ラグラジアンのこの不定性のために正準変換の具体的計算もできるのですが、
このラグラジアンの不定性が、ガリレイ変換に対する運動方程式の共変性をも保証します。
でもここまで制限を緩めてしまうと、もう何でもありです。
そもそもどうして、式(20)から運動方程式が得られなければならないのでしょうか?。
式(18)のラグラジアンの一般的形だけからなら、
式(18)の具体的な形がラグラジアンLではなくエネルギーE(ハミルトニアンH)でも、
運動方程式は、
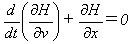 (22)
(22)
から得られます(形式的には(22)からも運動方程式が出ます)。
ラグラジアンから運動方程式が式(20)の変換方法に従って出てくる理由が、
少なくとも今までの議論にはありません。今までの議論とは、
ラグラジアンに力学に要請される一般的な制限を付けて形を絞っていくという話です。
つまり変換方法まで問題にすると、力学に要請される一般的な制限だけからは、
通常の形のラグラジアンを使用する必然性はなくなるということです。
これを防げる唯一の方法は、力学に要請される一般的な枠組みから、
ラグラジアンの形を定数倍と定数分の任意性くらいの不確かさで定めてやることですが、
たぶん不可能だと思います。
ところで式(20)はオイラー・ラグランジュ方程式で、
ある積分量を最小化する方法です。最初に言いましたように、
ラグラジアンが着想された根拠には「最小性へのこだわり」がありました。
では、ラグラジアンが最小量を導くものであることを要請した時に、
この事態は改善されないでしょうか?。
[3]ラグラジアンが最小量を導くものだとする
結論を言うと、改善されません。
何故なら最小化されるべきものはラグラジアン自身ではなく、作用積分、
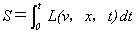 (23)
(23)
だからです。作用積分Sを最小化するべきだという理由がわからない限り、
式(20)の変換方法に達する理由もありません。
故ラグラジアンをわざわざ積分したものを最小化しなければ、
運動方程式にならないのでしょうか?。力学に要請される一般的な枠組みだけからは、
その理由は出てこないと思います(違ったら、ものすごく嬉しいです)。
あと考えられる立場としては、ラグラジアンは「運動ポテンシャル」なのだから、
何らかの方法で微分して運動方程式が導ければ良いのだ、
という立場です。でもこれはさっき言ったように、
式(18)の具体的形がラグラジアンではなくても、エネルギー(ハミルトニアン)
でも式(22)から運動方程式を導けるので、式(20)や、
ひいては通常の形のラグラジアンを要求するものではありません。
[4]ラグラジアンの出自
ではラグラジアンは、どこから生まれたのでしょう?。
個人的意見では「学生の全ての期待を裏切って、
誰かが論理的に導いたものではないために、
そのことがラグラジアンをひどく了解困難なものにしています」
結局このレポートでやりたいことは、ラグラジアンの意味を訪ねることなのですが、
今までやってきたような議論が昔なされなかったとは、絶対に思えません。
ただ、うまくいかなかったので、物理学の歴史書,教科書等には載っていないのではないかと
思う次第です。
ラグラジアンはどこから生まれたのか?。
次回の話ですが、これだけ色々やってきた後なので恐縮ですが、
もう殴られそうなくらい簡単に生まれてきたように思えます(後知恵の小賢しさでいえば・・・)。
[参考文献]
[1]ランダウ=リフシッツ,力学,東京図書
[2]大貫義郎,物理学テキストシリーズ2 解析力学,岩波書店
[3]大貫義郎・吉田春夫,現代物理学叢書 力学,岩波書店

 E-mail
E-mail
 戻る
戻る


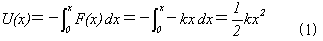
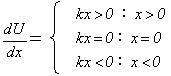 (2)
(2) となります。それを図化したものが、図-2です。x≠0では、常にx=0へ質点を引き寄せようと
する力が働き、一方x=0は正負の傾きの変わり目なので、
dU/dx=−F(x)=0となり、質点には力が働きません。よって質点は、
x=0以外には行きたくないし、いったんx=0にはまり込んだら、そこから出てきません。
これはx=0が静力学的釣り合い点であることをいってます。
しかしこれは、図-1の質点には外力が作用しないので、
バネは伸びないままという当たり前の結論でした。
そこで図-1の質点に紙面右向きの重力mgを作用させます(点線矢印)。
ポテンシャルエネルギーは、
となります。それを図化したものが、図-2です。x≠0では、常にx=0へ質点を引き寄せようと
する力が働き、一方x=0は正負の傾きの変わり目なので、
dU/dx=−F(x)=0となり、質点には力が働きません。よって質点は、
x=0以外には行きたくないし、いったんx=0にはまり込んだら、そこから出てきません。
これはx=0が静力学的釣り合い点であることをいってます。
しかしこれは、図-1の質点には外力が作用しないので、
バネは伸びないままという当たり前の結論でした。
そこで図-1の質点に紙面右向きの重力mgを作用させます(点線矢印)。
ポテンシャルエネルギーは、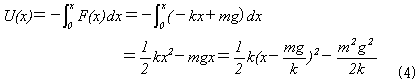

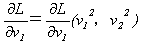 (10)
(10)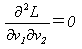 (11)
(11)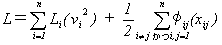 (16)
(16)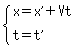 (17)
(17)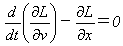 (20)
(20)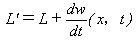 (21)
(21)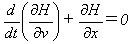 (22)
(22)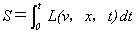 (23)
(23)
 E-mail
E-mail
 戻る
戻る