Weekend Mathematics乛僐儘僉僂儉幒乛NO.148
| NO.1254 | 2002.8.17. | DDT | 儔僌儔僕傾儞偺堄枴乮俁乯 |
儔僌儔僕傾儞偺堄枴(2)偺嵟屻偱丄儔僌儔僕傾儞偼傕偆丄
墸傜傟偦偆側偔傜偄娙扨偵惗傑傟偰偒偨偲彂偒傑偟偨
乮偁偔傑偱屻抦宐偺彫尗偟偝偱偡偑乯丅
偦偺偨傔偵偼抏惈妛偵婑傝摴偟偨傎偆偑椙偄傛偆偵巚偊傑偡丅
偙偙偱拲堄偡傋偒偼丄抏惈妛偲偼傆偮偆惷椡妛偱丄摦椡妛偱偼側偄偙偲偱偡丅
侾丏朹偺抏惈妛
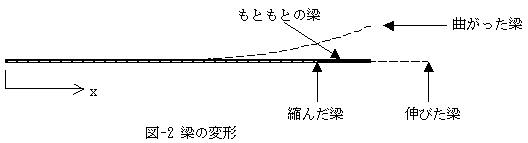
恾-1偺傛偆偵丄堦曽岦偵挊偟偔挿偄拰偺傛偆側傕偺傪椑偲屇傃傑偡丅

恾-1偺椑偺岤傒傪昞偡D傪椑偺怺偝偲偄偄丄椑偺慡挿L偵斾傋偰偠傘偆傇傫彫偝偄偲偟傑偡丅
偲偄偆偐丄偙偺忦審偑惉傝棫偭偨偲偒偵挿拰傑偨偼椑偲偄傢傟傑偡丅
椑偱偼D曽岦偺嵽椏偺嫇摦偼柍帇偟偰偄偄偙偲偑傢偐偭偰傑偡
乮D/L乣0傛傝丅L偲摨掱搙偺戝偒偝偺曄宍偟偐峫椂偟側偄偲偄偆嬤帡棟榑乯丅
傛偭偰椑偼1師尦偺峔憿(?)偱偡丅偦偺曄宍傪昞偡偵偼丄
偺慡挿偵増偭偨1屄偺嵗昗x偱丄偠傘偆傇傫偱偡丅椑偼嬋偑偭偨傝丄怢傃偨傝弅傫偩傝偟傑偡丅

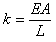 丂丂丂丂(1)
丂丂丂丂(1)
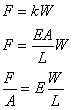 丂丂丂丂(2)
丂丂丂丂(2)

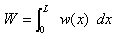 丂丂丂丂(4)
丂丂丂丂(4)
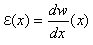 丂丂丂丂(5)
丂丂丂丂(5)
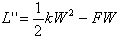 丂丂丂丂(7)
丂丂丂丂(7)
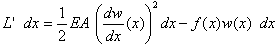 丂丂丂丂(8)
丂丂丂丂(8)
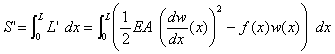 丂丂丂丂(9)
丂丂丂丂(9)
偙偙偱S'偼丄朹慡懱偺惷椡妛揑億僥儞僔儍儖乮惷椡妛揑側宯偺僄僱儖僊乕乯偱偡丅
S'傪嵟彫壔偡傟偽丄(4)偺朹慡懱偺掁傝崌偄曽掱幃偑弌傞偼偢偱偡丅
偱傕丄S'偺嵟彫壔偭偰壗偱偟傚偆丠丅
傑偢惷椡妛偵偍偗傞乽栤戣傪夝偔偙偲乿偺堄枴傪専摙偟傑偟傚偆丅
恾-4偵偍偄偰丄暘晍椡f(x)偼応強偛偲偵乮x偛偲偵乯曄傢傞傕偺偱偟偨丅
偩偐傜曄埵w(x)傕応強偛偲偵曄傢傝傑偡丅媡偵尵偊偽丄x偵娭偡傞曄埵暘晍w(x)偝偊掕傔偰偟傑偊偽丄
栤戣偼夝偗傑偡丅幚嵺偦偺偲偒幃(3)偐傜丄墳椡冃(x)偺暘晍傕傢偐傝傑偡丅
偍傛偦惷椡妛偵偍偄偰媮傔偨偄偙偲偼丄掁傝崌偆帪偺椡偲丄掁傝崌偆帪偺曄埵偵恠偒傑偡丅
冃(x)偲偼丄朹偺奺晹暘偵摥偔椡偺尵偄姺偊偱偁傝丄
兠(x)亖dw(x)/dx偲偼丄朹偺奺晹暘偺曄埵偺尵偄姺偊偩偭偨偙偲偵拲堄偟偰壓偝偄丅
傛偭偰(9)傪嵟彫壔偡傞偲偼丄
(9)傪嵟彫壔偡傞娭悢w(x)傪媮傔傛丏
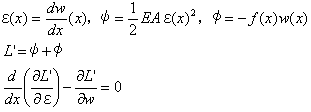 丂丂丂丂(10)
丂丂丂丂(10)
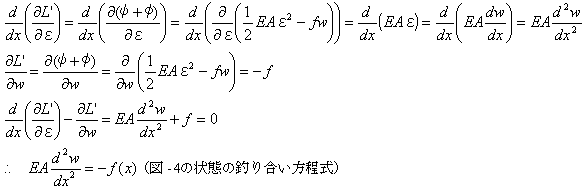 丂丂丂丂(11)
丂丂丂丂(11)
 丂丂丂丂(12)
丂丂丂丂(12)
 丂丂丂丂(13)
丂丂丂丂(13)
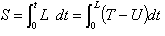 丂丂丂丂(14)
丂丂丂丂(14)
俀丏偄偄偺偐偙傟偱丠
侾丏偱傗偭偨偙偲偼丄偙偆傑偲傔傜傟傑偡丅
乽楢懕懱偺惷椡妛偵偍偗傞朹偺掁傝崌偄曽掱幃傪丄
乽嵟彫惈乿偵偙偩傢偭偰摫偄偨丅偦偺夁掱偱儔僌儔僕傾儞偲宍幃揑偵摨摍側傕偺
傪尒偮偗偰偟傑偭偨丅
傛偭偰偦偙偱尒偮偗偨儔僌儔僕傾儞偼丄乽嵟彫惈乿偺梫審傪枮偨偡偺偱塣摦億僥儞僔儍儖偩乿
偄偄偺偐偙傟偱両丠丅
偩偄偨偄朹偺惷椡妛偲幙揰偺摦椡妛偲偵丄偄偭偨偄偳傫側榑棟揑偮側偑傝偑偁傞偲偄偆偺偩両丅
偦傝傖儔僌儔僕傾儞傪偄偒側傝揤壓傝偵掕媊偝傟傞傛傝傕偄偔傜偐擺摼偱偒傞偗偳丄
宍幃揑懳墳偺傒偵婎偯偄偰儔僌儔僕傾儞偺宍傪尒偮偗偨屻偱傕偄偄偐傜丄
偦偙偐傜儔僌儔僕傾儞偺堄枴傪栤偆偰偄偔偺偑暔棟妛偺杮斣偱偼側偄偺偐丠丅
偦偺捠傝偩偲巚偄傑偡丅
偟偐偟楌巎揑偵偼偙偺傛偆側帠懺偱丄
彮側偔偲傕昞棫偭偰儔僌儔僕傾儞偺堄枴偑栤傢傟偨偙偲偼側偐偭偨偺偱偡丅
傕偪傠傫乵儔僌儔僕傾儞偺堄枴(1)乶偱弎傋偨傛偆側揘妛揑堄枴偼丄
偦偺宍幃揑懳墳偯偗偵廫暘偡偓傞掱惙傝崬傑傟傑偟偨偑
乮側傫偲嵟廔揑偵偼20悽婭弶摢傑偱懕偄偰傑偡乯丄
侾丏偱朶椡揑偵娙棯壔偟偨傛偆側帠懺偑楌巎揑偵偼嬶懱揑偵婲偙傝傑偟偨丅
妛惗偺慡偰偺婜懸傪棤愗偭偰丒丒丒丅壗屘側傜丄
嘆儔僌儔僕傾儞偑拝憐偝傟偨崻嫆偼乽姰慡柍寚偺恄條偑憿偭偨塅拡偺嵟彫惈乿 傊偺偙偩傢傝埲奜偵偼側偔丆
嘇扤偐偑榑棟棫偰偰摫偄偨傕偺偱傕側偔丆
嘊悢棟揑栶妱埲奜偺儔僌儔僕傾儞偺堄枴偑栤偆偙偲偼柍堄枴
嘆'偦偺懚嵼偼慜採側偺偱丄塣摦傪寛掕偡傞嵟彫検偼偁傟偽壗偱傕椙偔丆
嘇'偦傟偵婥偯偗偽椙偄偺偱扤偐偑摫偔昁梫傕側偔丆
嘊'儔僌儔僕傾儞偺堄枴偼恄條偑偮偗偰偔傟傞偺偱栤偆昁梫偼側偄
嶲峫暥專
[1] 嶳嶈媊棽丆廳椡偲椡妛揑悽奅丆尰戙悢妛幮
偙偺杮偼椡妛巚憐巎偱偁傞偲偲傕偵丄戝妛嫵梴壽掱偺屆揟椡妛梅侥偲偟偰廫暘捠梡偡傞偔傜偄偺
棟榑揥奐偑娷傑傟偰傑偡丏戝妛偵擖偭偨偢傇偺慺恖偺崰丄偙偺杮偱島媊偟偰梸偟偐偭偨丅
暘岤偄偗偳丅巓枀曇偵乽擬妛巚憐偺巎揑揥奐乿偑偁傝傑偡丏摨偠偔尰戙悢妛幮丏
偙偺2嶜偼偲偰傕椙彂偩偲巚偄傑偡丏崱偱偼懄暔惈偺戙柤帉偺傛偆側棟榑暔棟妛
乮 仼 傑偭丄巹偼傾儅僠儏傾偱偡偐傜乯偱偡偑丄偙傫側偵傕巚憐偑偮偄偰傑傢偭偨偺偐偲丄
偁傜偨傔偰巚偄抦傜偝傟傑偡丏巚憐偲偼丄棟榑偺堄枴傪朘偹傞偲偄偆偙偲偩偲巚偄傑偡丏
偦偟偰帺慠擣幆偺媶嬌偵偮偄偰偼丄25悽婭慜偺僊儕僔儍恖傕尰戙恖傕慡慠曄傢傜側偄偙偲偑傢偐傝傑偡丅
報徾揑偩偭偨偺偑幮夛妛幰僂僃乕僶乕傪堷梡偟偨晹暘偱偡丏
乽恖娫偼廳椡偑壗屘揱傢傞偐偼壗堦偮抦傜側偄偔偣偵丄偦傟偑偳偺傛偆偵揱傢傞偐傪抦偭偨偺傒偱丄
恖岺偺惎傪憿偭偨丅偦傟偼偲偰傕婏柇側偙偲偱偼偁傞偗傟偳傕丄偲偰傕嬤戙揑側偙偲偩丅
偦傟偑乽杺弍偐傜偺悽奅夝曻乿偲偄偆偙偲偱偁傝丄壗傕暔棟妛偩偗偵偼尷傜側偄丅
乽杺弍偐傜偺悽奅夝曻乿偲偼僂僃乕僶乕偺尵梩偱偁傞乿

| NO.1255 | 2002.8.17. | Junko | 僱僀僺傾偺晄摍幃乮俀乯 |
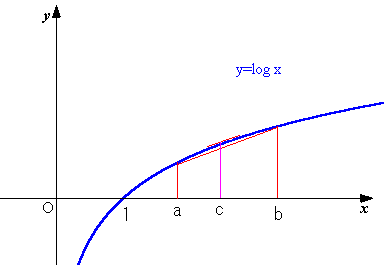
乮侾乯暯嬒抣偺掕棟偵傛傞徹柧
倖(倶)亖倢倧倗倶偲偍偔丅倶亜侽偱扨挷憹壛丅倖'(倶)亖侾乛倶丅
倖(倶)偼乵倎丆倐乶偱楢懕丄乮倎丆倐乯偱旝暘壜擻側偺偱暯嬒抣偺掕棟偵傛傝丄
倎亙佄們亙倐偵懳偟偰丄
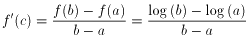
堦曽丄倖'(倎)亖侾乛倎丄倖'(倐)亖侾乛倐
倖'(倶)亖侾乛倶偼丄扨挷尭彮偩偐傜丄倖'(倐)亙倖'(們)亙倖'(倎)丄偮傑傝
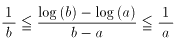
乮俀乯旝暘偵傛傞徹柧
倖(倶)亖倢倧倗倶偲偍偔丅
俙(倎丄倢倧倗倎)丄俛(倐丄倢倧倗倐)偲偡傞偲丄
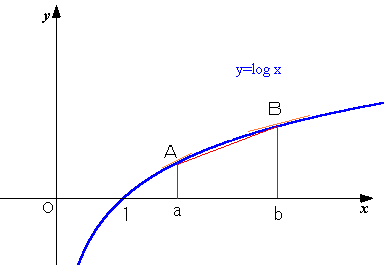
慄暘俙俛偺孹偒偼丄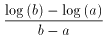
倷亖倖(倶)偼丄倶亜侽偵偍偄偰扨挷憹壛丄偐偮倖'(倶)亖侾乛倶亜侽傛傝忋偵撌丅
廬偭偰丄揰俛偵偍偗傞愙慄偺孹偒亙慄暘俙俛偺孹偒亙揰俙偵偍偗傞愙慄偺孹
偡側傢偪丄
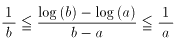
乮俁乯愊暘偵傛傞徹柧
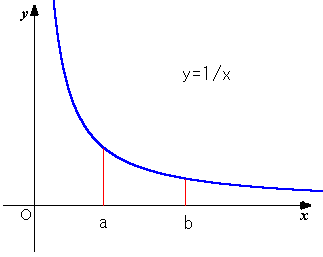
倖(倶)亖侾乛倶偲偍偔丅倶亜侽偵偍偄偰扨挷尭彮丅
乵倎丆倐乶偵偍偄偰丄
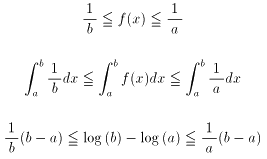
廬偭偰丄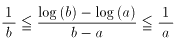

| NO.1256 | 2002.8.20. | BossF | 僱僀僺傾偺晄摍幃乮俁乯 |
[僱僀僺傾偺晄摍幃]乧偙偺僱僀僺傾(僱僀僺傾悢偺僱僀僺傾偩偲巚偄傑偡偑乯偺桼棃
偼丄側傫偱偟傚偆偐?
娬榖媥戣
偲傝偁偊偢丄懳悢偺掙偼僱僀僺傾悢偲偟偰峫偊
埲壓a,b 偼 0<a<b 傪枮偨偡傕偺偲偟傑偡丅
徹柧侾丗暯嬒抣偺掕棟傪梡偄偰
[夝]
倖(x)=lon x 偲偍偔偲丄
倖(x) 偼 [a,b] 偱楢懕丄偐偮 (a,b) 偱旝暘壜擻偱偡偐傜
暯嬒抣偺掕棟傛傝
佄c ; a<c<b 偐偮 {倖(b)-f(a)}/(b-a)=f'(c) (=1/c)
傑偨丄y=1/x 偺扨挷惈偐傜 1/b<1/c<1/a
傛偭偰戣堄偼帵偝傟傑偟偨丂仭
徹柧俀丗旝暘傪棙梡偟偰
[夝]
b-a>0 傛傝
梌幃佁1-a/b<lon(b/a)<b/a-1
傑偢丄嵍曈<拞曈 傪帵偟傑偡
f(x)=lon x + 1/x -1 (x>0) 偲偍偔偲
| f'(x) | =1/x - 1/x2 |
| =(x-1)/x2 |
師偵丄拞曈<塃曈 傪帵偟傑偡
f(x)=x-1-lon x (x>0) 偲偍偔偲
| f'(x) | =1 - 1/x |
| =(x-1)/x |
徹柧俁丗愊暘傪棙梡偟偰
[夝]
f(x)=1/x 偲偟傑偡偲丄偦偺扨挷惈傛傝
[a,b] 偱 1/b亝 f(x) 亝1/a 偱偡偐傜丄
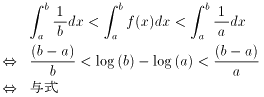
丂丂丂丂丂傛偭偰戣堄偼帵偝傟傑偟偨丂仭
偲丄偙偙傑偱彂偄偰傆偲尒偨傜丄偡偱偵僄儗僈儞僩側夝朄偑傾僢僾偝傟偰傞偱偼偁傝
傑偣傫偐乧乮丱丱丟丟
偨偩丄梋寁側摍崋乮亙佀亝 偵側偭偰傑偡乯偑偮偄偰傑偡偑丅

| NO.1257 | 2002.8.26. | 倳倱倎們們倛倝 | 帺慠尰徾偲悢妛偺娭學偵偮偄偰乮侾乯 |
悢妛偺愭惗偐傜偺幙栤偵偳偺傛偆偵摎偊偰傛偄偺偐暘偐傜側偐偭偨偺偱丄奆偝傫偺堄尒傪暦偒偨偄偺偱偡偑傛傠偟偄偱偟傚偆偐丠
帺慠尰徾偺墱偵偼岞幃乮俥倧倰倣倳倢倎乯丄朄懃乮俴倎倵乯丄尨棟乮俹倰倝値們倝倫倢倕乯側偳偲屇傋傞壗偐偑懚嵼偟偰偄傞偲巚偄傑偡偐丠
巹偼懚嵼偟偰傞偲巚偆偺偱偡偑丄偦偙偺偲偙傠偑敊慠偲偟偡偓偰愢柧偑偱偒側偄偺偱崲偭偰偄傑偡丅

| NO.1258 | 2002.8.26. | DDT | 抐柺偑忢偵墌偱偁傞棫懱恾宍乮俀乯 |
棫懱恾宍偺栤戣偱偡丅偁傞暵嬋柺偑偁傝丄偦偺嬋柺偑暯柺偱愗抐偝傟傞偲偒偺抐柺偑忢偵墌偱偁傞偲偒丄偙偺暵嬋柺偼媴偱偁傞偙偲傪徹柧偟偰偔偩偝偄丅
乵曽恓乶
偩傜偩傜峫偊偰偄偨傜丄4偮傎偳曽恓偑弌偰偒傑偟偨偑丄巹偵幚峴壜擻側偺偼嵟屻偺堦偮偱偟偨丅
嘆 旝暘婔壗妛傗懡條懱偺抦幆偑朙晉側応崌
栤戣偺忦審偐傜掕僈僂僗嬋棪丄偔傜偄偺偙偲傪娙扨偵帵偟偰乽億儞僢両乿偲摎偊傪弌偡丅
佀偙偺暘栰偼昿斏偵嵙愜偟偰傞偺偱丄柍棟丅
嘇 懳徧惈傪棙梡偡傞応崌
媴偺拞怱傪嵗昗尨揰偵慖傫偩応崌丄媴偼姰慡側摍曽惈傪帩偭偰偄傞丅
偡側傢偪媴柺嬌嵗昗偱r亖const丅師偵擟堄偺愗抐暯柺偱抐柺偼墌丅
墌偼偦偺拞怱偵懳偟偰姰慡側摍曽惈傪帩偭偰偄傞丅
偡側傢偪尨揰偑抐柺墌偺拞怱偵偁傝丄愗抐暯柺偵増偭偨嵗昗宯偺暯柺嬌嵗昗偱r'亖const丅
慜屻偺嵗昗宯偼丄捈岎傾僼傿儞曄姺偱堏傝偆傞乮柧傜偐偵寁検傪曄偊偰偼偄偗側偄乯丅
儀僋僩儖偺挿偝|r|偼丄捈岎傾僼傿儞曄姺偺晄曄検丅偙偺偁偨傝偺寁検偺摨宆惈偐傜摎偊傪弌偣偦偆丅
佀偱傕昁梫側寁検偺峔惉偺巇曽偑傢偐傜側偄丅傗偭傁傝柍棟丅
嘊 埵憡揑偵夝偔応崌
栤戣偺忦審偐傜丄媮傔傞嬋柺偼僩乕儔僗偲摨憡偱偁傞偙偲傪摫偔乮敊慠偲惓偟偄婥偑偡傞乯丅
僩乕儔僗偺捈宎傪娷傒丄僩乕儔僗偺忔傞暯柺偵悅捈側擟堄偺曽岦偺暯柺偱愗抐偟偨応崌丄
抐柺偼2屄偺墌偵側傞丅擟堄偺曽岦偱2屄偺抐柺墌偑廳側傞僩乕儔僗偑媴偱偁傞偙偲偼丄傎傏柧傜偐丅
媴偲摨憡偑昁梫忦審偲側傞偐傜丄媴偱側偐偭偨傜偲壖掕偟偰柕弬傪摫偒丄摎偊傪弌偡丅
佀乽柍棟丄柍棟乿乽偱偒傞傢偗偑側偄乿
嘋 栤戣偺懳徧惈傪棙梡偟偰丄弶摍婔壗妛揑偵張棟偡傞丅
佀乽僆僢丠丅偱偒傞傫偠傖側偄偐丠乿
乵嘋偺幚峴乶
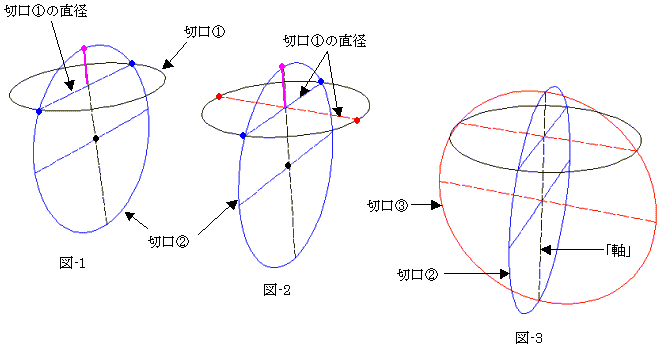
恾-1偺傛偆偵丄偁傞愗抐暯柺嘆偱愗偭偨愗岥傪崟墌偱昞偟丄愗岥嘆偲偟傑偡丅
愗岥嘆偺拞怱偼丄愗岥嘆偺忔傞愗抐暯柺嘆忋偵偁傝傑偡丅愗抐暯柺嘆偲捈岎偟丄
愗岥嘆偺拞怱傪捠傞傛偆側愗抐暯柺嘇偺愗岥傪惵墌偱昞偟丄愗岥嘇偲偟傑偡丅
愗岥嘆偼丄媮傔傞嬋柺偺嫬奅忋偵偁傞偙偲偐傜丄愗抐暯柺嘇偲愗岥嘆偺岎揰傪丄愗岥嘇偼捠傝傑偡丅恾-1偺惵揰偱偡丅偲偙傠偑愗抐暯柺嘇偼丄愗岥嘆偺拞怱傪捠傞偺偱丄惵揰偼愗岥嘆偺捈宎乮惵慄暘乯偲墌偱偁傞愗岥嘆偲偺岎揰偱偁傝丄愗岥嘆偺拞怱偐傜愗抐暯柺嘆偵悅捈忋曽偵怢偽偟偨僺儞僋儔僀儞偼丄愗岥嘇偲昁偢岎傢傝傑偡乮僺儞僋揰乯丅僺儞僋儔僀儞偑愗岥嘆偺捈宎偺2摍暘慄偱偁傞偙偲偐傜丄愗岥嘇拞怱偼丄僺儞僋儔僀儞偺壓曽墑挿忋偵偁傝傑偡乮崟揰乯丅
師偵愗抐暯柺嘇偲堘偆曽妏偵丄愗抐暯柺嘊傪偲傝傑偡偑丄愗抐暯柺嘊傕愗岥嘆偺拞怱傪捠傝丄愗抐暯柺嘆偵悅捈偲偟傑偡丅愗抐暯柺嘆丆嘇偺娭學偲慡偔摨偠偙偲偑丄愗抐暯柺嘆丆嘊偺娫偵惉傝棫偮偺偱丄愗抐暯柺嘊偺愗岥嘊偼丄恾-2偺愒揰偲僺儞僋揰傪捠傝傑偡丅摨堦暯柺忋偺3揰乮3揰側偺偱摨堦暯柺忋偼柧傜偐偱偡乯傪捠傞墌偼拞怱埵抲傑偱娷傔偰桞堦偵寛傑傝丄愗岥嘇偺惵-诉莞-惵揰偺攝抲偲丄愗岥嘊偺愒-诉莞-愒揰偺攝抲偑摨堦側偺偱丄愗岥嘇偲嘊偼摨偠敿宎傪帩偪傑偡丅偐偮僺儞僋儔僀儞偺壓曽墑挿忋偵偦偺拞怱偑偁傞偺傕摨偠側偺偱丄愗岥嘇偲嘊偼拞怱傪嫟桳偟傑偡丅傛偭偰恾-3偲側傝傑偡丅廬偭偰丄愗岥嘊偼僺儞僋儔僀儞傪拞怱幉偲偟偰丄愗岥嘇傪揔摉偵夞揮偝偣偨傕偺偱偡丅
埲忋偺偙偲偼丄愗岥嘆傪捠偭偰愗抐暯柺嘆偵悅捈側擟堄偺曽妏偺愗抐暯柺偱惉傝棫偮偺偱丄媮傔傞嬋柺偼恾-3偺乽幉乿傪夞揮幉偲偟偨丄愗岥嘇偺墌偺夞揮柺偲側傝媴偱偡丅

| NO.1259 | 2002.8.28. | Junko | 帺慠尰徾偲悢妛偺娭學偵偮偄偰乮俀乯 |
悢妛傕娷傔偰帺慠壢妛乮尰徾乯偵偮偄偰丄恖娫偑偦傟傪擣抦偱偒傞偐偳偆偐偼暿栤戣偱偡偑丄
偁傞朄懃丄尨棟偑摥偄偰偄傞偲巚偄傑偡丅
偦傟傪恖娫偑擣幆偱偒傞傋偔尋媶偟偰偒偨偙偲偑恖椶偺楌巎側偺偱偼側偄偐偲巚偄傑偡丅
擣幆偱偒偨帠暱偼丄恖娫偑棟夝偱偒傞曽朄偱昞尰偝傟偰偄傞傢偗偱
偡偑丄恖娫偑抦偭偰偄傛偆偲偄傑偄偲丄兾乮墌廃棪乯偼懚嵼偡傞偟丄
偦傟傪昞尰偡傞偺偵丄兾偲屇傏偆偑丄倶偲屇傏偆偑丄偦傟偼杮幙揑
側偙偲偱偼側偄偲巚偄傑偡丅
枹抦偺揤懱偐傜偺棃朘幰偲僐儈儏僯働乕僔儑儞傪偲傞偲偟偨傜丄
悢妛傪夘偡傞偺偑堦斣偄偄偲偄偆榖偟傕偁傞丠
乽恄偑僟僀僗傪怳傞偲偼偲偆偰偄怣偠傜傟側偄乿偲偄偆傾僀
儞僔儏僞僀儞偺桳柤側偙偲偽偑偁傝傑偡偗傟偳丄
偮傑傝嬼慠惈偵巟攝偝傟傞傕偺偑懚嵼偡傞偲偄偆偙偲偱偡偑丄
偙傟偡傜傕乽晄妋掕惈尨棟乿偭偰偙偲偵側傞傢偗偱偡傛偹丅

 E-mail
E-mail
 栠傞
栠傞