
Weekend Mathematics/コロキウム室/NO.132
| NO.1124 | 2002.1.7. | Junko | 関数列の極大点(2) |
(1)
(2)
以上から、an=1/2(n−1)と推定できる。
数学的帰納法で証明する。
| fk’(x) | =−k(k−x)k−1{x−1/2(k−1)}+(k−x)k |
| =(k−x)k−1(k+1)(−x+1/2k) |

| NO.1125 | 2002.1.11. | woops | 偽コイン探し |
12月の天秤の問題に似た問題なんですが、去年の暮れに友人から聞いてはまりました。
最初は頭の中でモヤモヤと、しまいには鉛筆と紙でウーンていう感じでした。
どうやら正解は何通りもありそうですが、紹介します。
どこからの出典だかわかりません。
有名な問題なんでしょうか?
12個のコインがある。その中の1つのコインだけが重さの違う偽物である事が わかっている。天秤を3回だけ使って、偽物のコインを探し出す手順を示せ。 (偽物のコインは本物よりも重いのか軽いのかはわかっていない。)

| NO.1126 | 2002.1.11. | Toshiro | ガウス記号(1) |
いきなりですいませんがガウス記号について学校に発表することになりましたのでガ
ウス記号について教えて下さい。

| NO.1127 | 2002.1.12. | Junko | ガウス記号(2) |
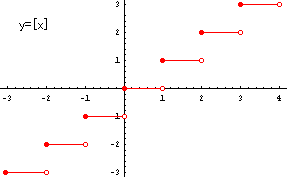
ガウス記号[x]は、xを越えない最大の整数を与えます。
例えば、[1.5]=1,[3]=3,[24/5]=4,[-1.8]=-2 です。
正の数に対しては、切り捨てと同じことになりますが、負の値の時は注意が必要です。
関数y=[x] を考えると、そのグラフは右のようになります。
ややむずかしい話しになりますが、この関数はすべての整数値で不連続となります。
詳しい話しは、NO.514、NO.536
をご覧になってみてください。

| NO.1128 | 2002.1.12. | 本多欣亮 | ゼーター関数 |
1月4日の日経夕刊に
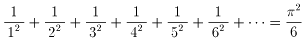
の話題が出ておりまして、「どうやったら導けるのだろう?」と
調べておりましたら、貴ページをある方から紹介されました。
すっきり氷解して、感謝感激です。
コメント(Junko)
詳しくは、コロキウム・テーマ別の部屋ゼ−タ−関数物語

| NO.1129 | 2002.1.14. | 水の流れ | 交代級数の和・その2 |
前回に続き、次のような無限級数の和を求めています。
今回は、必要な関数は見つけて、考えてください。
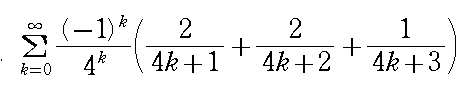

| NO.1130 | 2002.1.15. | Junko | 3次関数のグラフ(1) |
みっちの隠れ家の第2回問題
下のグラフはある3次関数のグラフです。
関数の式をy=ax3+bx2+cx+dとします。
このとき係数a,b,c,dの符号を求めてください。
答えは「a>0、b<0、c>0、d>0」
aの符号判定は、もちろんx→∞のときy→∞から
微分をして、y=3ax2+2bx+c=0(*)とおき、この2次方程式の解を
α、βとおきます。
グラフが極大点、極小点をx>0のところに持つことから、α、βは実数かつ正。
2次方程式(*)の解と係数の関係から、
α+β=−2b/3a>0
αβ=c/3a>0
これより、b<0、c>0
またグラフとy軸との交点の位置からd>0

| NO.1131 | 2002.1.16. | 水の流れ | 3次関数のグラフ(2) |
別解がありますよ。投稿します。
解法
y=ax3+bx2+cx+d=f(x)とおく。
aの正負の求め方は同じです。
ここで、yの導関数を求めると、f’(x)=3ax2+2bx+c となり、
f’(0)=c で、y=f(x)と y軸との交点での接線の傾きはグラフから右あがりだから、
f’(0)>0 ∴c>0
また、第2次導関数 f’’(x)=6ax+2b となり、
f’’(0)=2b で、y=f(x)と y軸との交点での凹凸はグラフから上に凸だから、 f’’(0)<0 ∴b<0
f(0)=d で、y=f(x)とy軸との交点はグラフからx軸の上にあるから、f(0)>0 ∴d>0
以上 すべてグラフから正負は判断できます。

| NO.1132 | 2002.1.17. | 月の光 | 交代級数の和(2) |
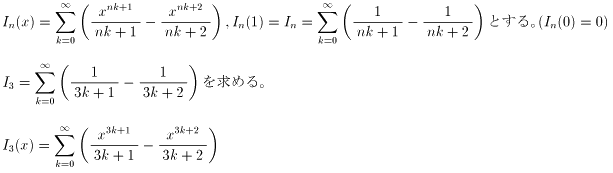
微分して
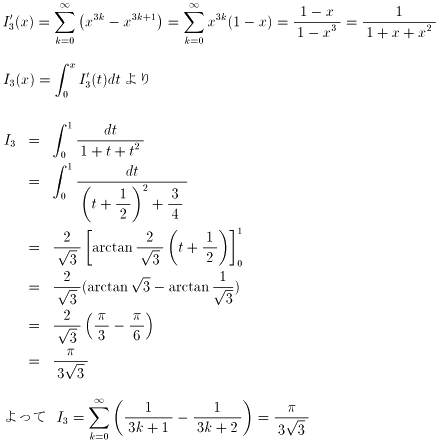

| NO.1133 | 2002.1.20. | 月の光 | 交代級数の和(3) |
他のn≧1についても求めてみました。
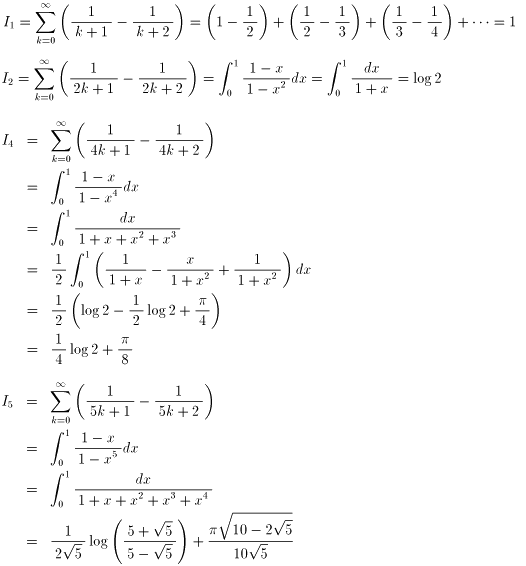
I5は途中の計算がノート5ページ程になるので省略します。
I5までは同様の方法で計算しましたがそれ以上は面倒だったので一気に
Inを考えました。
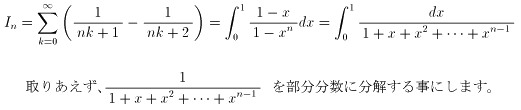
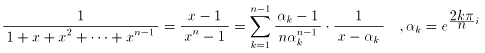

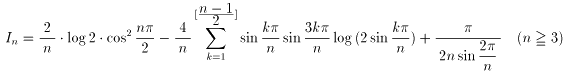
となりました。途中の計算は複雑で大変なので省略しました。
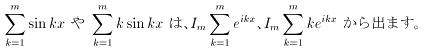
ただし、Imzは、”zの虚部”を表します。
つまり、Im(a+bi)=b
いくつか計算した結果を書いておきます。
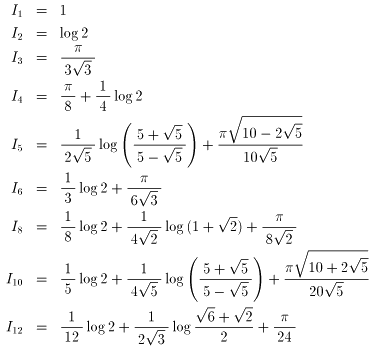
I9を計算しようとしましたが、sin(π/9)がわかりませんでした。
どなたか教えてください。
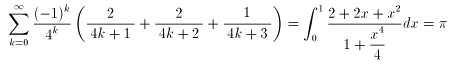
も同様に求まります。

| NO.1134 | 2002.1.20. | Junbou | フラクタル図形 |
ある本を読んでいて極限の問題にぶつかりました。内容は以下の通りです。
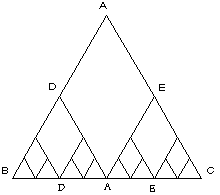
1辺の長さが1の正三角形ABCにおいてAB+AC=2(当然・・・)
今、頂点Aを辺BC上にくるように折りたたむ。無論頂点Aは辺BCの中点にくる。
また辺AB、ACは中点で折れる。それらの点をD、Eとする。
このときももちろんDB+DA+EA+EC=2となる。
そしてまた点D、Eから辺BCに折りたたむ。この操作を繰り返す。
するとはじめAB+AC=2だったのが辺BC=1に近づいてるように思える。
しかし、これは誤りである。このことを説明できませんか?
また、この操作で描かれた図形はフラクタル図形なのですか?
もしよろしければ解答をお願いします。

 E-mail
E-mail
 戻る
戻る