
Weekend Mathematics/コロキウム室/NO.127
| NO.1077 | 2001.11.1. | Idaho Potato | あみだくじ |
4本の「縦線」の間に、10本の「(梯子の段にあたる)横線」を書き込んで
「あみだくじ」を作りました。
このあみだくじについて、くじの結果 (入口と出口の対応関係) を変える
ことなく、さらに5本の「横線」を書き加えることはできるでしょうか?

| NO.1078 | 2001.11.2. | yokodon | 正三角形の内部を動く線分(8) |
No.1076 の浜田さんのお答えで正解です((^人^) パチパチ)。
ここでは、余弦定理から得た条件式の対称性を活用した別解をご紹介したいと思います。
なお、AP= p 、AQ= q とさせて下さい。
まず、
a2 = p2 + q2 - pq …[1]
ですね。
p , q は、いずれも0と2のあいだを動くので、
u = p + q 、v = pq
とおくと、p,q は以下の2次方程式の0〜2のあいだの実数解(重解を含む)となり
ます。
t2 - ut - v = 0
この左辺を f(t) とおいて、そのような p,q が存在するための条件は、
f(0) > 0 、f(2) > 0 、0 <(軸)< 2 、(判別式)≧ 0
です。これを、u 及び v の式に直すと、以下です。
v > 0 、4 - 2u + v > 0 、0 < u/2 < 2 、u2 - 4v ≧ 0 …[2]
[1]式を u , v の式に書き直すと、以下です。
a2 = u2 - 3v …[3]
[2] および [3] の両式から、まず u の値域を求めます。
両式から v を消去し、
a < 3 - √(a2-3) < 3 + √(a2-3) < 2a < 4
に注意して整理すると、その値域は以下です。
a < u < 3 - √(a2-3) 、 3 + √(a2-3) < u ≦ 2a …[4]
この [4] のもとで u の関数 v ( v = 1/3・(u2 - a2) )の取りうる値域は、
この両区間で v が u の関数として単調増加であることに注意して、
0 < v < 2・{1 - √(a2-3) 、
2・{1 + √(a2-3)} < v ≦ a2
となります。
三角形APQの面積をSとすると、S=√3/4・v ですから、最終的に以下の結果
を得ます。
0 < S < √3/2・{1 - √(a2-3)} 、
√3/2・{1 + √(a2-3)} < S ≦ √3/4・a2
以前の No.1020 『動く正三角形』と同様、
対称性に着目すると基本対称式の活用
で解決できる(cf. No.1037)という問題でした。

| NO.1079 | 2001.11.4. | 水の流れ | 囲まれた面積 |
今、太郎さんは学校で積分法を教えています。過去の入試問題を眺めていたら、東京工業大学に次のような問題がありました。
少し改題して紹介します。
第1象限内の曲線:xa+yb=1とx軸、y軸で囲まれた部分の面積をSとする。
問題1:a=b=2のとき、曲線は円になる。このときの面積Sを求めよ。
問題2:a=b=1のとき、曲線は直線になる。このときの面積Sを求めよ。
問題3:a=b=1/2のとき、曲線は放物線になる。このときの面積Sを求めよ。
問題4:a=b=2/3のとき、曲線はアステロイドになる。このときの面積Sを求めよ。
ここからが、入試問題です。
m,nを自然数とする。第1象限内の曲線:x1/m+y1/n=1とx軸、
y軸で囲まれた部分の面積をS(m,n)とする。
問題5:S(m,1)を求めよ。
問題6:S(m,n+1)をS(m+1,n)とm,nを用いて表せ。
問題7:S(m,n)をm,nを用いて表せ
(別解はベーター関数を利用しても解けます)

| NO.1080 | 2001.11.5. | 高橋 道広 | できるでしょうか? つづき(4) |
NO.1050 できるでしょうか
「7×7の正方形の内部及び周上に50個の点を、どの2点間の距離も1.5以上離して 書くことが出来るでしょうか」というような問題でした。
解説
この7×7の正方形を1×1の小正方形49個に分割する線を引きます。
どの49個の小正方形の内部及び周上にも1つしか点がないとすると、点は高々49個し
かないことになりますから、内部及び周上に2個以上の点を含む正方形が必ずありま
す。このとき、正方形の対角線の長さは、√2=1.4...ですから、この正方形の内部の2点
の距離は1.5を超えません。よって 「出来ません」 が答えです。m(__)m

| NO.1081 | 2001.11.5. | ジュンボウ | どこが誤り? |
私は今、九州のある私立高校で教員をやっております。
この前生徒からある質問を受け、一応答えはしたものの自分自身納得いきません。
質問内容は:
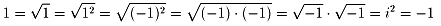
の式で誤っている部分を訂正して理由も答えよ。
という問題です。有名な問題ですが高校生にわかりやすく説明してください。
自分の勉強不足で申し訳ないのですがどうぞよろしくお願いします。

| NO.1082 | 2001.11.6. | Junko | あみだくじ(2) |
あみだくじは対称群をなし、横線は互換を与えます。
横線5本を書き加えるということは、互換5つの積、奇置換になりますから、くじの
結果は変わってしまいます。つまり不可能。

| NO.1083 | 2001.11.6. | Idaho Potato | あみだくじ(3) |
正確に言うと、横線を5本加えることによって、
あみだくじ全体の置換としての偶奇が変わる、ということです。
当然、問題中の「縦線4本横線10本」という設定に意味はありません。
言うまでもなく、書き加える横線の本数が偶数なら、同じ場所に続けて
書き加えれば、くじの結果は変わりません。
ところで、上述の解答は、対称群に関する次の知識を仮定しています。
この事実は、証明はさほど難しくありませんが、「自明」とはいえません。
ある置換を互換の積の形に表すとき、その表し方は一意的でないが、 互換の個数の偶奇は表し方によらず一意に定まる。
それから、解答では用いられませんが、次の事実も重要です。
すべての置換は互換の積の形に表せる。
このことから、もう少し強い次の事実が成り立つことは容易にわかります。
すべての置換は「隣り合う要素の互換」の積の形に表せる。
(「隣り合う」とは、対称群のunderlying setを {1,2,...,n} と考えたときの 隣り合う自然数のこととする)
あみだくじの横線は「隣り合う要素の互換」を与えますから、これは、
「すべての置換はあみだくじで表現できる」という主張にほかなりません。
ついでに言うと、与えられた置換に対して、隣り合う要素の互換の積による
具体的な表現 (i.e. あみだくじによる表現) を得るためのアルゴリズムが
「バブルソート」です。

| NO.1084 | 2001.11.6. | BossF | どこが誤り?(2) |
これは、根号の規約の問題ですね
「負の数の平方根は、a>0のとき
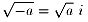 」
」
と定義されているからです…説明になってないかな?

| NO.1085 | 2001.11.6. | Junko | どこが誤り?(3) |
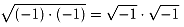
この部分が誤りですね。つまり
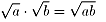
が成り立つのはa>0,b>0の時に限るわけです。
当たり前のような定理ですが、その条件をしっかり確認しないと足元をすくわれるという例ですね。

| NO.1086 | 2001.11.9. | BossF | 囲まれた面積(2) |
問題1
半径1の円の1/4ですから π/4 …答
問題2
対角線の長さが2の正方形の1/4ですから
1/2 …答
問題3
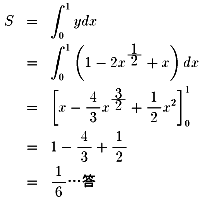
問題4
x=cos3θ , y=sin3θ とおけることに注意します
第一象限の面積Sは
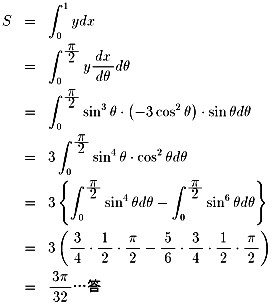
問題5
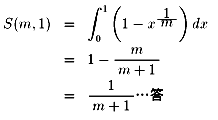
問題6
x=cos2mθ, y=sin2nθとおけることに注意します。
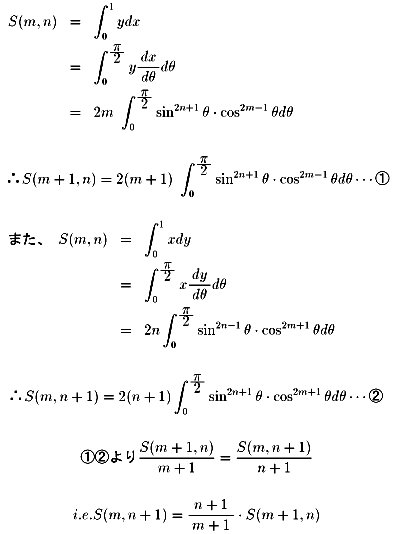
問題7
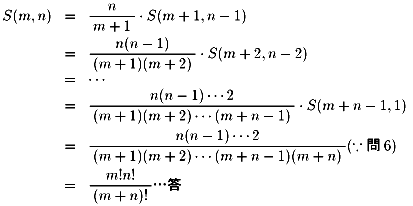

| NO.1087 | 2001.11.9. | yokodon | 囲まれた面積(3) |
後半の問5以降に関して、投稿致します。
結局、以下の積分を実行すればいいのですよね。
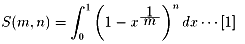
問5:上記で、n = 1 の場合です。
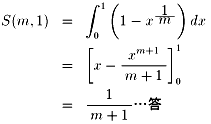
問6:まず、[1] 式を変形します。
x = sin2mu とおくと、以下のようになります。
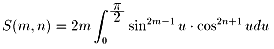
更に、t = sin(u) とおくと、以下のようになります。
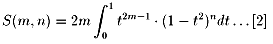
[2] 式の右辺を部分積分することで、以下を得ます。
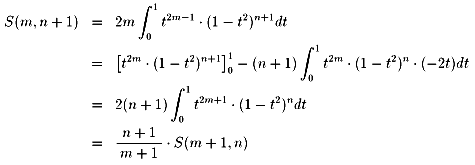
従って、結論は以下です。
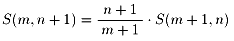
問7:問6の結果を繰り返し用いて、以下を得ます。
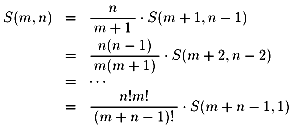
問5の結果から、
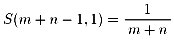
なので、結局求める値は、
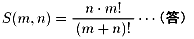
B関数で表すと、S(m,n) = m・B(m, n+1) でしょうか。

| NO.1088 | 2001.11.9. | 夜ふかしのつらいおじさん | どこが誤り?(4) |
これは BossF さん「どこが誤り?(2)」のいうように
「根号の規約の問題です」
「1」は「実数の1」です。「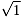 」は「1の正の平方根」です。
」は「1の正の平方根」です。
「√」の記号の前に符号の「+」が省略されています。
「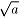 」と「a1/2」とは「a」が負でない実数のときは同じ意味になります。
」と「a1/2」とは「a」が負でない実数のときは同じ意味になります。
しかし、「a」が複素数のときには、意味が異なります。
これは極形式で考えると分かりやすいと思います。
1=cos(2nπ)+i・sin(2nπ) (n:整数)
としてみます。
| {cos(2nπ)+i・sin(2nπ)}1/2 | |
| = | cos(nπ)+i・sin(nπ) |
| = | +1(n:偶数のとき),−1 (n:奇数のとき) |
「a」が複素数のとき「a1/2」とは「2乗してaになる数」です。
−1=cos((2n+1)π)+i・sin((2n+1)π) (n:整数)
としてみます。
| {cos((2n+1)π)+i・sin((2n+1)π)}1/2 | |
| = | cos((n+1/2)π)+i・sin((n+1/2)π) |
| = | +i(n:偶数のとき),−i(n:奇数のとき) |
「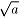 」は「aの平方根のうち正のもの」ですが、「a」が複素数のときには、
「a1/2」は、実数の正とか負の概念は消えてしまいます。
」は「aの平方根のうち正のもの」ですが、「a」が複素数のときには、
「a1/2」は、実数の正とか負の概念は消えてしまいます。
「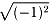 」は、演算に順番があります。「2乗」が先になり「√」が後になります。
ですから、負でない実数を考えているときは問題が起こりません。
」は、演算に順番があります。「2乗」が先になり「√」が後になります。
ですから、負でない実数を考えているときは問題が起こりません。
また「{(−1)2}1/2」では、演算の順番は制約がなくなります。
| {(−1)2}1/2 | |
| = | [{cos((2n+1)π)+i・sin((2n+1)π)}2]1/2 |
| = | {cos((4n+2)π)+i・sin((4n+2)π)}1/2 |
| = | cos((2n+1)π)+i・sin((2n+1)π) |
| {(−1)1/2}2 | |
| = | [{cos((2n+1)π)+i・sin((2n+1)π)}1/2]2 |
| = | {cos((n+(1/2))π)+i・sin((n+(1/2))π)}2 |
| = | cos((2n+1)π)+i・sin((2n+1)π) |

 E-mail
E-mail
 戻る
戻る