コロキウム室

この数列を定義にしたがって、求めてみました。

a₁ ＝２　

これより１／a₁＋１／ｘ＜１、１／２＋１／ｘ＜１、つまりｘ＞２となる。
これを満たす最小の自然数は３だから、a₂ ＝３　

同様に１／a₁＋１／a₂＋１／ｘ＜１、１／２＋１／３＋１／ｘ＜１、つまりｘ＞６
これを満たす最小の自然数は７だから、a₃ ＝７　

同様にa₄ ＝４３・・・　
何となくイメージは持てました。

（1）次の等式が成り立つことを示せ。

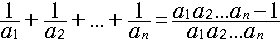
数学的帰納法で示します。

• n=1のとき
  （左辺）＝１／a₁＝１／２
  （右辺）＝(a₁−１)／a₁＝１／２　よりＯＫ
  
  
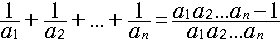• 　が成立していると仮定する。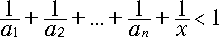
  
  
• a_n＋１は、以下の不等式を満たす最小の自然数ｘで与えられる。
  
  
  これより、

  1/ｘ	＜ 1−(1/a1 + 1/a2 +…+ 1/an)
  	＝１−(a1・a2・・・an−１)／a1・a2・・・an
  	＝１／a1・a2・・・an
  ｘ	＞a1・a2・・・an

  
  
  従ってこれより、a_n＋１＝a₁・a₂・・・a_n＋１
  
  さて、

  （左辺）	＝1/a1 + 1/a2 +…+ 1/an＋１
  	＝(a1・a2・・・an−１)／a1・a2・・・an+ 1/an＋１
  	＝(a1・a2・・・an＋１−an＋１＋a1・a2・・・an)／a1・a2・・・an・an＋１
  	＝(a1・a2・・・an＋１−１)／a1・a2・・・an＋１
  	＝（右辺）

  
  

（2）異なる自然数 k, l に対し、a_k と a_l は互いに素であることを示せ。

a_n＋１＝a₁・a₂・・・a_n＋１より、

a_n＋１はすべてのa_ｋ(１≦ｋ≦ｎ)と互いに素であることがわかる。
よって題意は示された。

第８４回数学的な応募問題

大垣市内にある高層建物は１階（地上階）から１７階まであり、各階の間は等間隔です。 エレベーターで１階から５階まで直行したら、１６秒かかりました。
１階から11階まで直行したら、２６秒かかりました。 奇妙に見えますが、次のような考え方をすると、理解できます。
このエレベーターは加速減速が遅く、動き出してから最大速度に達するまで、 一定の加速度で動く。減速し始めてから停止するまでも一定の加速度で減速し、 停止するまでには、動き出してから最大速度に達するまでと同じ時間が必要。 中間は一定の最大速度で動くが、もし移動距離が短いと、 最大速度に達しないうちに減速して、目的階に達する。ここで、問題です。

問題１：このエレベーターの加速度を求めよ。

問題２：動き出してから最大速度に達するまで、何秒かかりますか。

問題３：動き出してから最大速度に達したとき、エレベーターは何階と何階の間にいるでしょうか。

問題４：１階から16階まで直行するとき、何秒かかりますか。

問題５：１階からＮ階まで直行するとき、何秒かかるか、Ｎで表せ。

後半の（2）は、丁寧にやるなら例えば以下でしょうが、ここの常連の皆さんにと っては常識レベルでしょうか？

k ＜ l として良い。
そのもとで、（1）の結果より、
a_l ＝ a₁・…a_k…a_l-1 +1 　・・・[1]
と表せる。
ここで、a_k と a_l の最大公約数を p とすると、 ある自然数 b_k および b_l が存在して、
a_k ＝ p・b_k 、a_l ＝ p・b_l
と表せる。これを上式に代入して整理すると、
p・(b_l - a₁・…b_k…a_l-1) ＝ 1　・・・[2]
となるが、[2] の左辺は自然数同士の積なので、p ＝ 1 である。

本問で僕が面白いと思ったのは、以下の２点です。

−1−比較的単純なルールで、素数を“生成”できる。
（ii）の条件式から、反復的にドンドン素数を作れるというのは、初見の時にはあ る意味で驚きでした。
こちらの以前のコンテンツで“素数の逆数の総和は発散する”と言うのがあったと 思います。
（少し計算すると分かることではあるのですが）本問のルールのもとで計算できる 素数は、あくまで素数全体の一部なのですが、Σ1/a_k（和は１〜∞にわたる）が１ に収束するような部分集合を具体的に計算していると言うことになります。

−2−２項間漸化式で、素数を計算できる。
｛a_n｝に関する多項間漸化式を、２項間漸化式に書き直すことが出来ます。結果は、
a_n+1 ＝ a_n² - a_n +1
です。これで、いくらでも大きな素数を具体的に計算できます（コンピューターやア タマがちゃんと動きさえすれば）。
というわけで、実は本問（1）の等式と、
a₁ ＝２ 、a_n+1 ＝ a₁・…・a_n + 1
及び
a₁ ＝２ 、a_n+1 ＝ a_n² - a_n + 1
の３者は、同値です。

題意にしたがって、順にａ₁＝２、ａ₂＝３、 ａ₃＝７、ａ₄＝４３、 ａ₅＝１８０７、ａ₆＝３２６３４４３、・・・・となります。
ａ₁、ａ₂、ａ₃、ａ₄ は素数です。
しかし、ａ₅＝１８０７＝１３×１３９ で合成数になるのではないでしょうか。
また、ａ₆ も素数です。
ａ₇以上は面倒なので見ていません。
異なる ａ_k とａ_l とが互いに素は、確かだと思いますが、ａ_k そのものが素数と は限らないということだと思います。

今月の問題　できるでしょうか？ に関連して・・・
7cm×7cmの正方形の内部に50個の点を適当に書くときに、どの２点の距離も1.5cmよ り短く出来るでしょうか。どこかでお目にかかった問題です。(~_~;)

・・・アラ、地道に計算してみると、確かにそうですね（落ち着いて考えてみれば 、その通り；道理で、話がうますぎると思ったら・・・）。
手計算の時には、第６項で爆発的に大きくなってしまったのは覚えていて、そこで 手計算を挫折した記憶があるのですが、全ての a_n（n ＝ 1,2,...）が互いに素だか らといって、各項が素数とは限らないのですね。
第５項が合成数なのは、気が付きませんでした（大ボケですね）。
ついでに、手元の MathCad 6.0 for Mac で計算してみたら（第７項の算出とわり 算）、
a₇ ＝ 10650056950807 ＝ 549×607×1033×31051
でした。良い勉強になりました。
なお、計算に際しては、以下の手を借りました。

素数かどうか判定するプログラムver.3.0
（16 桁までの整数について、素数か否か判定できるようです）

#そうなると｛a_n｝の素因数分解で、全ての素数を尽くせ るのでしょうか？（その辺が、興味あるところです。）

長さの単位を階間（F）とし（→；それがないと、加速度の単位が定義できません ので）、エレベータの運動を考えることにします。先に、エレベータの運動を速度に 関して解いておきましょう。エレベータの加速度を a とします。

（i）途中で等速運動にならない場合

速さが最大になるまでの所要時間を t₀ とすると、 止まるまでの時間は 2・t₀ 。
速さを v として、それぞれの時刻で、

v ＝	at　　　　　　（0 ≦ t ≦ t0）、
	a・(t0 - t) （t0 ≦ t ≦ 2・t0）

となります。

（ii）途中で等速運動になる場合

速さが最大になるまでの時間を t₀ 、停止する時刻を T とします。速さ v は

v ＝	at　　　　　　（0 ≦ t ≦ t0）
	a・t0　　 （t0 ≦ t ≦ T - t0）
	a・(T - t)　 （T- t0 ≦ t ≦ T）

となります。

上記の速さに関する式を、時刻に関して積分すれば変位になります。容易に計算で きるので全ては示しませんが、(ii) の３番目だけ示せば、変位 x は
x ＝ a・t₀・(T - t₀) - 1/2・a・(T - t)² となります。

では、解答を進めます。

（1）2F 進むあいだに８秒かかっている。この場合は (i) に相当する。
よって、2 ＝ 1/2・a・8² から、a ＝ 1/16（= 0.0625） F/sec² …（答）

（2）10F 進むあいだに 26 秒かかっており、上記 (ii) で T = 26 の場合に相当する。
積分の結果を用いて、
10 ＝ 1/2・a・t₀・{26 + (26-2・t₀)}
から、（1）の結果を用いて、t₀ ≦ 13 に注意して解くと、 t₀ ＝ 10 sec …（答）

（3）t ＝ t₀ のときの位置を求めればよい。
（1）（2）と積分の結果から、
1/2・a・t₀² ＝ 25/8（∈［3,4］）。
よって、４階と５階のあいだ…（答）

（4）求める時間を T として、（1）（2）と積分の結果から、
15 ＝ a・t₀・(T - t₀)
これに、a ＝ 1/16 、t₀ ＝ 10 を代入して整理すると、T ＝ 34 sec …（答）

（5）同じく、求める時間を T として、
N-1 ＝ a・t₀・ (T - t₀)
これに、a ＝ 1/16 、t₀ ＝ 10 を代入して整理すると、以下を得る。
Ｔ＝（8N+42）/5 sec …（答）

ただし、(8N+42)/5 -20 の正負（∵問（2）より加速時間の最大値は 10 秒）で、場合分けがやっぱり必要かも知れません。
途中に等速運動がある場合の結果は T ＝ (8N+42)/5 で良いはずですが、その条件 は“(8N+42)/5 -20 ≧ 0”から N ≧ 8 ですね。
N ≦ 7 の場合は、T ＝ 4・√(N-1) （sec）ですね。

計算間違いがあったらスミマセン。 積分しなくとも、速度-時間のグラフで面積を出すと変位になることが理解できて いれば良いのでしょうね。

�@5階に直行する場合�A11階に直行する場合、とし エレベーターの最大速度をVmaxとします。
また、これは、問題で指定されてないのですが 1階分の距離を１とします。
もう一つ、加速時と減速時の加速度も等しいとして、考えていきます。

さて
(i)�@�AいずれもVmaxに達しない場合
(ii)�@�AいずれもVmaxに達する場合
(iii)�AはVmaxに達するが、�@はVmaxに達しない場合 のいずれであるかを判定します。

各々の場合のv-t gragh が以下のfig1〜3です。

いずれも、
青線とｔ軸に囲まれた部分(�B)の面積=10
赤線とｔ軸に囲まれた部分(�C)の面積=4　
でなければならないことに注意します。

(i)の時、�B�Cは明らかに相似で、その比は13：8
ところが、面積比が5：2ですから、不適

(ii)の時、�B�Cの差（黄色で示した部分）は平行四辺形で面積が6ですから、 Vmax=0.6　
これを用いて�Cの台形の上底を求めてみますと
(x+16)x0.6x1/2=4 より　x=-8/3 となってしまいますから、不適

(iii)の時、�Bの台形の両側の線を延長して出来る三角形を考えます。（緑で示した 部分=�D）
�B+�Dは�Cと13：8の相似ですから、
�B+�D=4x169/64=169/16
∴�D=169/16-10=9/16
よって、�B�Dは面積比169：9 i.e. 13：3の相似
だから、�Bの上底=6
これより、(26+6)xVmax/2=10 i.e. Vmax=5/8
上の結果よりVmaxまで加速する時間とVmaxから停止するまでの時間の和は20秒…�E
その間に進む距離は�Cとの相似関係から 4x(20/16)²=25/4…�F
したがって16階に直行する時にかかる時間は
20+(15-25/4)÷5/8=34秒…問題4の答
�Fより、Vmaxまで加速しVmaxから停止するまでに動く距離は25/4=6.25
すなわちVmaxまで加速しそこから減速停止すると、7.25階に止まる事になります
したがって上と同様にしてN(≧8）階まで直行すると
20+(N-1-25/4)÷5/8=(8N+42)/5
またN(≦7)階まで ｔ (sec)とすると�Cとの相似関係より
16²：t²=4：N-1 ∴t=8{(N-1)^1/2}
まとめると
2≦N≦7の時、8{(N-1)^1/2}
8≦N≦17の時、(8N+42)/5 …問題5の答

(以下加速時と減速時の加速度も等しいと仮定して)
また�Cは二等辺ですから加速時間は8秒
よって加速度は
1/2xax64=2 より　1/16(sec^-2)…問題1の答
�Eより、Vmaxに達する時間は　10秒…問題2の答
�FよりVmaxに達した時進んだ距離は25/8=3.125
すなわち、4階と5階の間にいます…問題3の答

v-t graph の意味、加速度の意味、が分かっていれば、小学生にも解けますね（一部 を除いて）
よい問題だと思います　

（１）「ａ_n+1 の素因数分解で、すべての素数を尽くせるか？」について

つくせません。

ａ₁＝２
ａ_n+1＝ａ₁・ａ₂・・・・・ａ_n ＋ １

で決まる数 （２、３、７、４３、１８０７、３２６３４４３、・・・・）は ５ の倍数ではありません。

もし ａ_n+1 が ５ を因数に持つとすると、下１けたが、５ か ０ です。
しかし、ａ_n+1 は奇数なので、５ の場合が考えられます。
しかし、実際には ａ_n+1 の下１けたは ５ にはなりません。

ここで積の下１けたをあたえる演算を「＃」とします。（例　７＃９＝３）

	ａ2 の下１けた
＝	ａ1 ＋ １
＝	２ ＋ １
＝	３

	ａ3 の下１けた
＝	ａ1＃ａ2 ＋ １
＝	２＃３ ＋ １
＝	６ ＋ １
＝	７

	ａ4 の下１けた
＝	ａ1＃ａ2＃ａ3 ＋ １
＝	（ａ1＃ａ2）＃ａ3 ＋ １
＝	６＃７ ＋ １
＝	２ ＋ １
＝	３

	ａ5 の下１けた
＝	ａ1＃ａ2＃ａ3＃ａ4 ＋ １
＝	（ａ1＃ａ2＃ａ3）＃ａ4 ＋ １
＝	２＃４３ ＋ １
＝	６ ＋ １
＝	７

・・・・・・

	ａ2k+1 の下１けた
＝	ａ1＃ａ2＃ａ3＃・・・＃ａ2k-2＃ａ2k-1＃ａ2k ＋ １
＝	ａ1＃（ａ2＃ａ3）＃・・・＃（ａ2k-2＃ａ2k-1）＃ａ2k ＋ １
＝	２＃（３＃７）＃・・・＃（３＃７）＃３ ＋ １
＝	２＃（１）k-1＃３ ＋ １
＝	６ ＋ １
＝	７

	ａ2k+2 の下１けた
＝	ａ1＃ａ2＃ａ3＃ａ4＃ａ5＃・・・＃ａ2k＃ａ2k+1 ＋ １
＝	ａ1＃（ａ2＃ａ3）＃（ａ4＃ａ5）＃・・・＃（ａ2k＃ａ2k+1） ＋ １
＝	２＃（３＃７）＃（３＃７）＃・・・＃（３＃７） ＋ １
＝	２＃（１）k ＋ １
＝	２ ＋ １
＝	３

だから ａ_n+1 の下１けたは、３ または ７ となり、５ を因数にはもちません。

（２）「a₇ ＝ 10650056950807 ＝ 549×607×1033×31051」について これはどこかちがってます。

	５４９＃６０７＃１０３３＃３１０５１
＝	（（９＃７）＃３）＃１
＝	３＃３
＝	９

となり 10650056950807 の下１けたと一致しません。 最初の数が５４７のようです。

	（（７＃７）＃３）＃１
＝	９＃３
＝	７

E-mail 戻る