Weekend Mathematics乛僐儘僉僂儉幒乛NO.126
| NO.1074 | 2001.10.25. | 昹揷丂柧枻 | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俆乯 |
寁嶼偵傛傞摎偑弌偦傠偭偨偲偙傠側偺偱乮偄偮偺榖丠乯丆
偙偙偱僷僜僐儞偺僾儘僌儔儉偵傛傞夝摎傪搳峞偟傑偡丏
崱夞偼俧俼俙俹俤俽傪棙梡偟偰夝偄偰傒傑偟偨丏
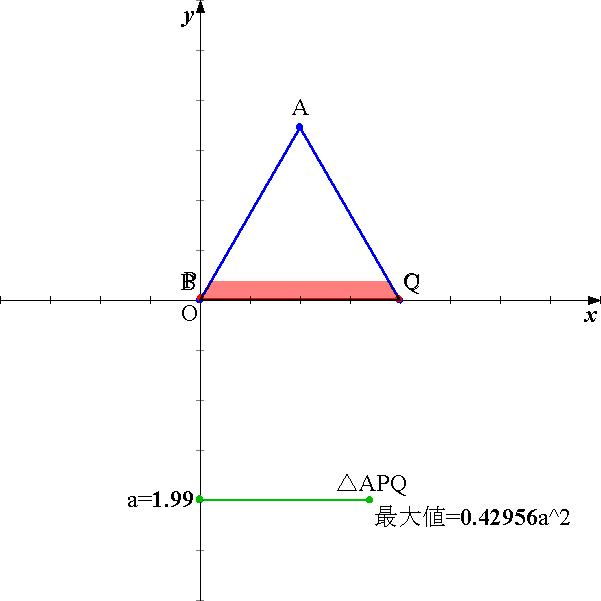
俙(侾丆併俁)丆俛(侽丆侽)丆俠(俀丆侽)丆俙俹亖倫丆俙俻亖倯丆
捈慄俙俛丗倷亖倖(倶)丆捈慄俙俠丗倷亖倗(倶)
偲偡傞偲丆
倖(倶)亖併俁倶丆倗(倶)亖亅併俁(倶亅俙倶)亄俙倷丆
俹(侾亅倫乛俀丆倖(俹倶))丆俻(侾亅倯乛俀丆倗(俻倶))丆
傑偨倫2亄倯2亅倫倯亖倎2丆倫亜侽丆倯亜侽偱偁傞偐傜丆
倯亖(倯亄併(係倎2亅俁倫2))乛俀
偲側傞丏
丂偙傟傜偺偙偲偑傜偐傜丆師偺俧俼俙俹俤俽偺僗僋儕僾僩傪嶌惉偟偰傒偨丏
# file://Click偱寁嶼奐巒 # clraimg # k:=.01 # for a:=Sqrt(3)+k to 2-k step k # t:=0 # for p:=k to 2-k step k # m:=Ax-p*.5 # q:=(p+Sqrt(4*a*a-3*p*p))*.5 # n:=Ax+q*.5 # if n<2 then # s:=.5*p*q*sin(Pi/3) # if t< s then # t:=s # u:=m # v:=n # endif # draw # endif # next # c:=u # d:=v # draw # next # ---


| NO.1075 | 2001.10.25. | BossF | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俇乯 |
乮^^丟丟Yokodon偝傫偺偍偭偟傖傞捠傝乧
乽傑偨丂p or q 仺0 偱丂pq仺0 偼偁偒傜偐乿偼堘偭偰傑偡偹丄埲壓掶惓
乽AP=p , AQ=q 偲偍偔丄
傑偢梋尫掕棟傛傝丂
a2=p2+q2-2pq丒cos60亱=p2+q2-pq
亪(p-q)2+pq=a2, i.e. pq=a2-(p-q)2乧嘆
偟偨偑偭偰丂pq亝a2
偙偙偱丄pq偺嵟彫抣傪峫偊傞丅
傑偢丄p亙q偲偟偰傕堦斒惈傪幐傢偢
嘆傛傝d=q-p偑嵟戝偺帪偵pq偼嵟彫偱偁傞偙偲偵拲堄偡傞丅
i) a亝併3偺偲偒
p偑梌偊傜傟傞偲堦斒偵q偼擇捠傝偁傞偑丄偦偺戝偒偄曽偺q傪峫偊傞丅
偁偒傜偐偵 p 仺0 偑壜擻偱丄偦偺偲偒 d仺Max
丂丂丂丂丂丂丂丂丂丂丂丂丂傛偭偰嵟彫抣側偟
ii)a亜併3 偺偲偒
q偑梌偊傜傟傞偲堦斒偵p偼擇捠傝偁傞偑丄偦偺彫偝偄曽偺q傪峫偊傞丅
偁偒傜偐偵 q 仺2 偑壜擻偱丄偦偺偲偒 d仺Max
丂丂丂丂丂丂丂丂丂丂丂丂丂傛偭偰嵟彫抣側偟
埲忋傛傝丂pq亝a2
偝偰
仮APQ=pq丒sin60亱x1/2=乮併3/4乯pq偩偐傜
仮APQ亝乮併3/4乯a2 (摍崋偼AP=AQ偺帪)乧摎乿

| NO.1076 | 2001.10.28. | 昹揷丂柧枻 | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俈乯 |
忦審偐傜丆
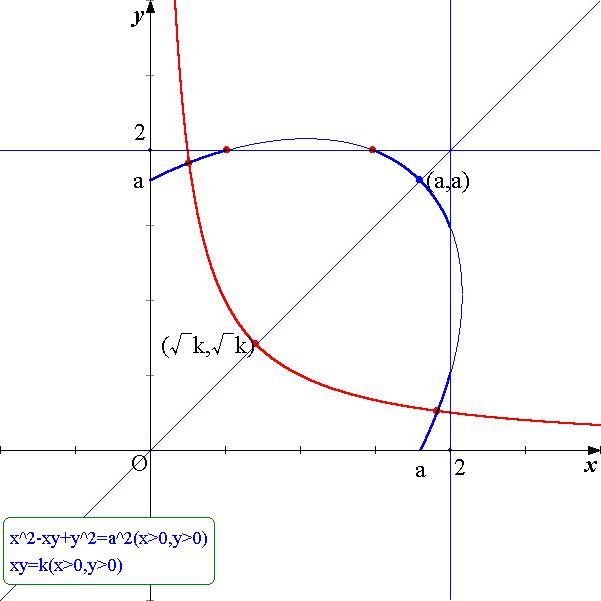
丂丂倶2亄倷2亅倶倷亖倎2乧乧乧(1)
丂丂侽亙倶亙俀丆侽亙倷亙俀丆併俁亙倎亙俀乧乧乧(2)
偵偍偄偰
丂丂倶倷亖倠
偺抣偺斖埻傪媮傔傟偽傛偄偙偲偑暘偐傞丏
丂倶丆倷偺懳徧惈偐傜丆倷亞倶偺斖埻偱峫偊傟偽傛偄丏
丂(1)偵偍偄偰丆倷亖俀偲偡傞偲丆
丂丂倶2亄係亅俀倶亖倎2
丂丂亪倶2亅俀倶亄係亅倎2亖侽
丂丂亪倶亖侾亇併(倎2亅俁)
丂丂丂丂丂丂丂丂丂丂乮塭偺惡丗偩偐傜倎亜併俁側傫偩両乯
丂偮傑傝捈慄倷亖俀偲嬋慄(1)偺岎揰偺嵗昗偼丆
丂丂(侾亇併(倎2亅俁)丆俀)
偱偁傞丏
丂僌儔僼偐傜
丂丂侾亅併(倎2亅俁)亝倶亝侾亄併(倎2亅俁)
偺斖埻偱偼丆倷亞俀偲側傝丆倷偼懚嵼偟側偄偙偲偑暘偐傞丏
丂屘偵倶倷偼丆
丂丂俀{侾亅併(倎2亅俁)}偐傜俀{侾亄併(倎2亅俁)}傑偱
偺斖埻偺抣傪偲傜側偄丏
丂僌儔僼偐傜丆
丂丂侽亙倶倷亙俀{侾亅併(倎2亅俁)}丆俀{侾亄併(倎2亅俁)}亙倶倷亝倎2
丂仮俙俹俻亖併俁乛係丒倶倷偱偁傞偐傜丆
丂丂侽亙仮俙俹俻亙併俁乛俀丒{侾亅併(倎2亅俁)}丆
丂丂併俁乛俀丒{侾亄併(倎2亅俁)}亙仮俙俹俻亝併俁乛係丒倎2

 E-mail
E-mail
 栠傞
栠傞