
Weekend Mathematics/コロキウム室/NO.120
| NO.1015 | 2001.9.1. | Junko | 10で割った余り(2) |
(1)
L(m)=L(n)=1 より、整数a,bを用いて、
m=10a+1、n=10b+1とかける。
| mn | =(10a+1)(n=10b+1) |
| =100ab+10a+10b+1 | |
| =10(10ab+a+b)+1 |
(2)
nは4の倍数なので、ある整数kを用いて、n=4kとかける。
3n=34k=(34)k=81k
(1)の結果より、
L(3n)=L(81k)=L(81)k=1k=1
これより、ある整数cを用いて、3n=10c+1とおける。
3^(3n)=310c+1=(310)c・31
=(59049)c・3
というわけで、整数cが偶数か奇数かで場合分けが必要なようです。
| 3^(3n) | =(59049)c・3 |
| ≡9c・3(mod 10) | |
| ≡92d・3(mod 10) | |
| ≡(92)d・3(mod 10) | |
| ≡1・3(mod 10) | |
| ≡3(mod 10) |
| 3^(3n) | =(59049)c・3 |
| ≡9c・3(mod 10) | |
| ≡92d+1・3(mod 10) | |
| ≡(92)d・9・3(mod 10) | |
| ≡9・3(mod 10) | |
| ≡7(mod 10) |

| NO.1016 | 2001.9.1. | やまし | カードシャッフル |
ある会社の採用試験で出た問題です。
n枚のすべて異なる種類のカードを用意する。
i枚のカードを上から取る。取ったカードの束を A、残ったカードの束をBと呼ぶ。
Aの底から一枚、Bの底から一枚、交互に一枚ずつカードをAとBより取り新しい束を作る。
最後にAかBで余ったカードはそのまま新しい束の上にのせる。
以上の操作でカードの束が最初の状態(順序)に戻るまでには、操作を何回繰り返せばよいか?
N=1001、i=100 として結果はどうなるか?

| NO.1017 | 2001.9.1. | 浜田 明巳 | 恒等式の解き方(3) |
NO.1004 前回の恒等式の問題で,出てきた2つの式
| 2x2−5xy−3y2+x+4y−1=(2x+y−1)(x−3y+1)………(1) | |
| 2x2−xy/3−3y2+x+4y−1=(2x+y−1/3)(x−3y+3) | |
| = | 2x2−5xy−3y2+17x/3+4y−1………(2) |
これらは,どちらも
2x2+axy−3y2+x+4y−1=(2x+y+b)(x−3y+c)………(3)
に
(x,y)=(0,0),(0,1),(1,1)………(4)
を代入して,定数a,b,cの値を得られてできた式でした.
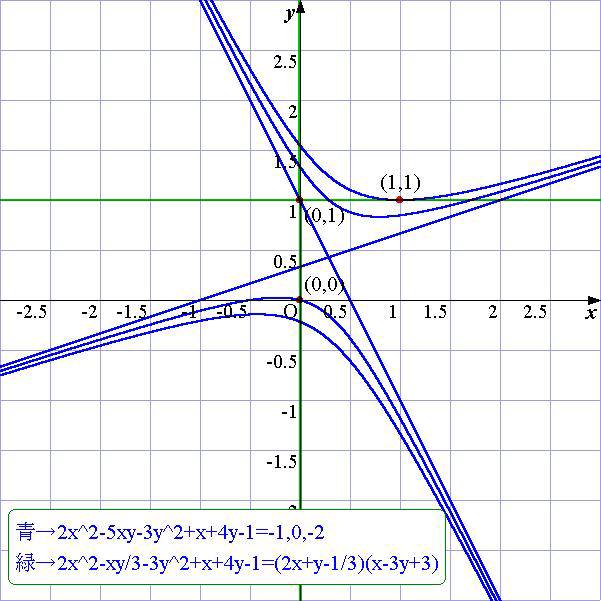
(1)はx,yの恒等式なのですが,(2)は(4)の3点を通る2直線を表します.
つまり,すべての点を通る曲線(つまり平面)を表す恒等式の係数を求める問題だったのですが,
計算の途中で,(4)の点を同時に通る曲線(2直線)が出てきてしまったようなのです.
これは,x,yの混合式において見られる現象だと思います.
xのみの式の場合,
(xのn次式)=(xのn次式)
型式の恒等式では,xのn次関数となるので,(n+1)個の異なるxの値を与えれば,
このxのn次式が一意的に定まります.
x,yの混合式の場合,陰関数となるので,そうはいかなくなります.
もっと複雑な要素がからんでくるのでしょう.
とにかく結論は,x,y(あるいはそれ以上の文字)の混合式の恒等式の問題で,
数値代入法で解く場合,単純に最後に
「逆にこのとき,最初の等式を満たす.」
と付け加えることは出来ず,最後まできちっと計算してチェックすべきだ,ということでしょうか.
私が大学を卒業し,教職につくとき,恩師(ゼミの先生)が言って下さいました.
「教室にはガウスがいる.手を抜くな.」※
まさにその通りです.
※大数学者ガウスは,小学生時代,先生から
1+2+3+………+100
を計算せよ,という課題を与えられました.先生とすれば,時間稼ぎに出した問題だったのです.
しかしガウス少年は,
| 2×(1+2+3+………+100) | |
| = | (1+100)+(2+99)+(3+98)+………+(100+1) |
| = | 100×101=10100 |

| NO.1018 | 2001.9.1. | 水の流れ | 三角形の面積比(1) |
太郎さんは、最近「ヴェイユ」さん頂いた「面積比」の問題を考えていたときに、
下のような問題を気がつきました。
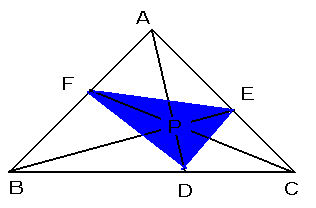
鋭角三角形ABCにおいて、内部に任意に点Pをとり、直線APと辺BCとの交点をD,
直線BPと辺CAとの交点をE,直線CPと辺CAとの交点をFとする。
また、「チェバ」の定理から、BF:FA=p:q,AE:EC=r:p,
CD:DB=q:rとおける。(ただし、p,q,rは正の数で、便宜的にp+q+r=1とする。)
このとき、
問題1:面積比、三角形DEF/三角形ABCの値をp,q,rで簡単に表してください。
さらに、ここで、BC=a,CA=b,AB=cとし、点Pが次のような場合、
p:q:rの比を辺a,b,cや角A,B,Cなどを用いて求めてください。
(ただし今回は、p+q+r=1の制約を取り除きます。)
問題2:点Pが重心の場合
問題3:点Pが内心の場合
問題4:点Pが外心の場合
問題5:点Pが垂心の場合
でも、点Pが問題2,3,4、5のときの面積比、
三角形DEF/三角形ABCの値がどうなるか気になります。
わかったら教えてください。

| NO.1019 | 2001.9.2. | yokodon | 10で割った余り(3) |
(2)について、僕が思い描いていた(&記憶及び理解している)のは、以下のようなモノです。
n = 4m(m:整数)とおくと、2項定理よりある自然数 j が存在して、
3n = 81m = (80 + 1)m = 80j + 1
が成り立つ。よって、L(3n) = 1 …(答)
後半は、この考え方を使うと、もっとすんなり行きます。
80 は4の倍数なので、上記同様にある自然数 k が存在して、
以下が成り立つ(但し、j' = 20j)。
| 3^(3n) | = 3(80j+1) |
| =3×3(4j') | |
| = 3×(80k+1) | |
| =10×24k+3 |
No.1015 にある整数 c が奇数となる場合は、実は存在しません
(上記の表現を借りれば、c = 8j になっています)。
結局、『n が4の倍数』であることが、最後までポイントとなる問題でした。

| NO.1020 | 2001.9.2. | yokodon | 動く正三角形 |
模試シリーズ3
一辺の長さが2の正三角形OABの辺AB、辺BO、辺OA上にそれぞれ点P、点
Q、点Rをとる。三角形PQRが常に正三角形であるという条件の下で三点P、Q、
Rが動くとき、線分QRの存在しうる領域の面積を求めよ。

| NO.1021 | 2001.9.2. | Junko | 三角形の面積比(2) |
問題1
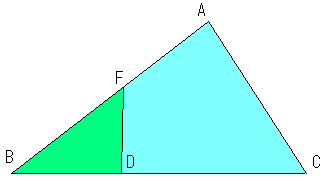
三角形ABCの面積は、S=1/2・BA・BC・sinBで求めることができます。
一方、角Bを共有している三角形BDFの面積は、
S’=1/2・BF・BD・sinBとなります。
従って面積比は、
S’/S=BF・BD/BA・BC=(BF/BA)・(BD/BC)
| 1−(q/(q+p)・r/(r+p)+p/(q+p)・r/(r+q)+q/(r+q)・p/(r+p)) | |
| = | 1−{qr(q+r)+pr(p+r)+pq(p+q)}/(p+q)(q+r)(r+p) |
| = | 2pqr/(p+q)(q+r)(r+p) |

| NO.1022 | 2001.9.2. | Hakuchonn | 無数の組み合わせ(1) |
夏休みを利用してピーターフランクルさんのセミナーに参加しました。その
ときの問題を2題:
〔問題〕
m2+1がnで割り切れ、n2+1がmで割り切れるような自然数の組
(m,n)は無数に存在することを示せ。

| NO.1023 | 2001.9.2. | Hakuchonn | 知り合い(1) |
〔問題〕
ある部屋に10人がいた。その中でお互いを知っている2人が11組だっ
た。このとき、お互いを全く知らない4人が選べることを示せ。

| NO.1024 | 2001.9.3. | kiyo | 無数の組み合わせ(2) |
F(1)=1,F(2)=1,F(n)=F(n-1)+F(n-2) フィボナッチ数列。
(M,N) (F(1),F(1))
M<N (F(2n-1),F(2n+1)) n>=1
不思議な数列ですね。

| NO.1025 | 2001.9.3. | kiyo | 知り合い(2) |
10人に1〜10の番号を付ける。
1−2,1−3,1−4,1−5
2−3,2−4,2−5
3−4,3−5
4−5
5−6
11組の知り合い。
7,8,9,10の4人はだれとも知り合いでない。

 E-mail
E-mail
 戻る
戻る