
Weekend Mathematics�^�R���L�E�����^NO.122
| NO.1036 | 2001.9.15. | ���̗��� | �ő�J�ʁi�P�j |
���Y����́A�W��20�E21���ɍs��ꂽ�u������ے��u�K��v�ɏo�Ȃ��Ă��܂������A
�����ς̕������̂悤�Ȑg�߂Ȗ����o����A�������܂����B�Љ�܂��B
���F�����̍ג����S��܂�Ȃ��āA�Ƃ������܂��B
�Ώ̂ɂQ�J���œ����p�x�ɐ܂�Ȃ��āA����r��`�ɂ��܂��B�i���̐}�j
�ǂ��łǂ̂悤�ɐ܂�Ȃ�����A�J���ł����ʂɗ������Ƃ��ł���ł��傤���B


| NO.1037 | 2001.9.16. | yokodon | �������O�p�`�i�S�j |
�@���̒�Ď҂Ƃ��āANO.1026,
NO.1031�ɕ⑫�����ĉ������B�l�c����ADDT
����A�����͗L���������܂����B
�@���͐����� ��3/3 �ł����A�̈�̋��E�������ƕ������ł��邱�Ƃ��������̂ł�
���A���̓r�����ꉞ������Ǝ����Ă��������Ǝv���܂��B�����������͍l�����
�܂����A�Q�ʂ肾�������܂��B
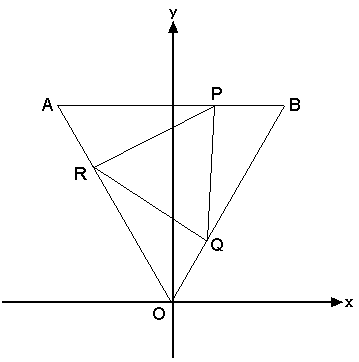 �@�Ƃ肠�����A�E�}-1�̗l�ɍ��W�n���Ƃ�܂��B�n�����_�Ƃ��A
�_�n��ʂ�A�����`�a�ɕ��s�Ȓ����� x ���A�_�n��ʂ�A����ɒ������钼���� y
���Ƃ��A[�`�a] �̌����� x ���̐������Ƃ��܂��B���̂Ƃ��A�Q�_�`�C�a�́A�ȉ���
�悤�Ɏ��܂��B
�@�Ƃ肠�����A�E�}-1�̗l�ɍ��W�n���Ƃ�܂��B�n�����_�Ƃ��A
�_�n��ʂ�A�����`�a�ɕ��s�Ȓ����� x ���A�_�n��ʂ�A����ɒ������钼���� y
���Ƃ��A[�`�a] �̌����� x ���̐������Ƃ��܂��B���̂Ƃ��A�Q�_�`�C�a�́A�ȉ���
�悤�Ɏ��܂��B
�` (-1 , ��3)�@�a (1 , ��3)
�����̂P�G�x�N�g�����g�����@��
�_�p�A�q���ȉ��̂悤�ɂƂ�܂��B
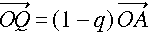 �A�@�@�@
�A�@�@�@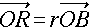 �A0 �� q, r �� 1
�A0 �� q, r �� 1
�@�O�p�`�o�p�q�����O�p�`�ł��邱�Ƃ���A�_�o�̈ʒu�x�N�g���́A��]�s���p��
�Ĉȉ��̂悤�ɕ\���܂��B
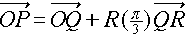
�A���AR(��/3) �͊p�x ��/3 �̉�]�s��i�����v���𐳕����Ƃ���j�ł��B
�@������A�����ŕ\���ƁA�ȉ��ł��B
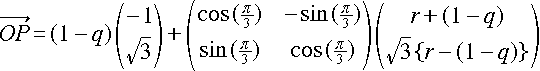
�@�_�o���A�����`�a��ɂ��邽�߂̏����́A�o (p1, p2) �Ƃ��āA�ȉ��ł��B
-1 �� p1 �� 1 �Ap2 ����3
�@��Q�̓������Aq �� r �܂��B��P�̕s�����́A���̂��ƂŎ����I�ɐ�����
�܂��B
�@����ŁANO.1031 �̋c�_�͐���������܂��ˁB
�@���āA�����p�q��̔C�ӓ_�� ( X , Y ) �Ƃ����ƁA�p�����[�^ l �i0 �� l �� 1
�j��p���āA�ȉ��̂悤�ɕ\���܂��B
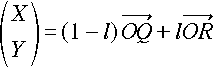
�@������A�����ŕ\���ƁA�ȉ��̂悤�ł��B
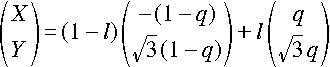
�@0 �� l, q �� 1 �̂��Ƃ� l �y�� q �������Ƃ��� ( X , Y ) �̑��ݔ͈͂����߂�
�A��ӂ̗̈�ɂȂ�܂��B
�@�㎮������ƁA�ȉ��܂��B
l + q �� X +1 �Alq �� 1/2�E(Y/��3 + X)
�@�]���āA�ȉ��̂Q���������� 0 �� u �� 1 �Ɂi�d�����܂߂āj�Q������������
�̕K�v�\�����������߂�A�̈�̎����o�Ă��܂��B
u2 - (X +1) u +1/2�E(Y/��3 + X) �� 0
�@��̂Q���������̍��ӂ� f(u) �Ƃ��āA���̏����͈ȉ��ł��B
f(0) �� 0 �Af(1) �� 0 �A0 ��(��) �� 1 �A (���ʎ�)��0
�@������AX �y�� Y �̎��ɏ��������ƁA�ȉ��̂悤�ɐ����ƕ������ň͂܂ꂽ�̈�
��\�����̂ɂȂ�܂��B
Y + ��3�EX �� 0 �AY - ��3�EX �� 0 �A
-1 �� X �� 1 �AY �� ��3/2�E(X2 + 1)
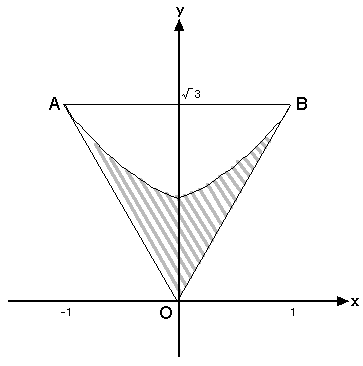 �@�}������ƁA�E�}-2�̗l�ɂȂ�܂��B�t��H��c�_�́A�ȗ���
���Ă��������܂��i���A�ǂ����K���ɂȂ�Ǝv���܂��j�B
�@�}������ƁA�E�}-2�̗l�ɂȂ�܂��B�t��H��c�_�́A�ȗ���
���Ă��������܂��i���A�ǂ����K���ɂȂ�Ǝv���܂��j�B
�����̂Q�F�������g�����@��
 �@�E�}-1 �̗l�ȓ_�z�u�̂��ƂŁA���`�o�q�߁��a�p�o�߁��n�q�p�ł��邱�Ƃ������܂��B
�@�E�}-1 �̗l�ȓ_�z�u�̂��ƂŁA���`�o�q�߁��a�p�o�߁��n�q�p�ł��邱�Ƃ������܂��B
�@�܂��A
�ڂ`�o�q+�ڂ`�q�o�� 2��/3�A�ڂ`�o�q+�ڂa�o�p�� 2��/3
�ł��邱�Ƃ���A�ȉ��܂��B
�ڂ`�q�o���ڂa�o�p
�@����Ɠ��l�̋c�_���J��Ԃ��āA���Ljȉ��܂��B
�ڂ`�q�o���ڂa�o�p���ڂn�p�q�A
�ڂ`�o�q���ڂa�p�o���ڂn�q�p
�@���o�p�q�����O�p�`�ł��邱�Ƃ���A��L�̍������������܂��B
�@����āA�`�q���a�o���n�p ���܂��B
�@���Ƃ͓K���Ƀp�����[�^���߂ŁA��L�g���̂P�h�Ɠ��l�̋c�_�ŖړI�̗̈��
�邱�Ƃ��o���܂��B
�@���ɁA�_�o�̍��W�œ_�p�y�ѓ_�q�̍��W��\���A�����p�q�̑|�߂���̈���Q����
�n�`�A�n�a�Ő����Ă��Ƃ������j������ł��傤�B
�g���̂P�h�̓_�̉�]�́A
���f���ʂɂ����� exp(2��i/3) ��K���ȕ��f���ɂ����Z���邱�Ƃł��������܂��ˁB
�����́A�P���ɂo�p���p�q���q�o�ł���Ă���Ԃ͂��܂�ς��Ȃ��̂ł́H
 �@�ꉞ�A�Ō�܂Ō����Ă����܂��傤�B
�E�}-2 �̍��W�y�ыȐ��\���̂��ƂŁA���߂�
�ʐςr�́A�ȉ��̂悤�ɋ��܂�܂��B
�@�ꉞ�A�Ō�܂Ō����Ă����܂��傤�B
�E�}-2 �̍��W�y�ыȐ��\���̂��ƂŁA���߂�
�ʐςr�́A�ȉ��̂悤�ɋ��܂�܂��B
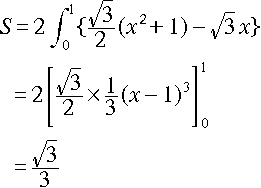

| NO.1038 | 2001.9.20. | �n���@�� | �H�v�́i�P�j |
�u�H�v�́v
�N���������������鎞�ɁA������p�x���炱�̉ۑ�����߂Ă���
�ʂȉ�����́B�Ǝ��͍l���Ă��܂��B
���āA�v�Z���Ă������Ȃ��ۑ�ł��A�H�v���Ă��������B
[���S�@�c�R�̒����`������܂��B �Ίp���̒����́�o�i�S�~�S�j�{�i�R�~�R�j}����Q�T�Ǝ�����܂��� ����ł́�i�S�~�R�j����P�Q�͂ǂ̒����Ƃ��Ď������ł��傤���H]

| NO.1039 | 2001.9.20. | �c�c�s | �ő�J�ʁi�Q�j |
���F�����̍ג����S��܂�Ȃ��āA�Ƃ������܂��B�Ώ̂ɂQ�J���œ����p�x�ɐ܂�Ȃ��āA ����r��`�ɂ��܂��B �i�}-1�j�ǂ��łǂ̂悤�ɐ܂�Ȃ�����A�J���ł����ʂɗ������Ƃ��ł���ł��傤���B
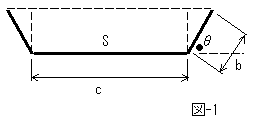 2b�{c��a
2b�{c��a
�[�̐܂�Ȃ��� b
�܂�Ȃ��p�x ��
�Ƃ��̖ʐ� S
�m���j�n
�P���ɂƂ��̖ʐύő���ƍl���܂��Bb�ƃƂɂ��Ă̋ɑ�l�����߂�B
�mb�͈̔́n
2b�{c��a�i��const.�j���c��a�|2b�ŁA0��c��a������A
0��b��a/2 (1)
�m�Ƃ͈̔́n
����b�ɑ��ăƂ�90������ƁA�}-1���A�Ƃ��̖ʐς͌���̂ŁA
0���Ɓ���/2 (2)
�m�Ƃ��̖ʐ�S�n
���[�̎O�p�`�Ƃ܂�Ȃ��̒����`�̖ʐς𑫂��A
S��b2cos��sin�Ɓ{bc�sin��
�ł��B2b�{c��a�i��const.�j�Ȃ̂ŁA
S(�ƁCb)��b2cos��sin�Ɓ{b(a�|2b)�sin��
�m��S/�݃Ɓn
��S/�݃Ɓ�2b2cos2�Ɓ{b(a�|2b)cos�Ɓ|b2 (3)
(3)�̉E�ӂ�f(cos��)�Ƃ����ƁAcos�ƂɊւ���Q�����ŁA(2)���0��cos�Ɓ�1�B
f(0)���|b2��0 �i(1)���j
f(1)��b2�{b(a�|2b)��0�i(1)���j
�Ȃ̂ŁAf(cos��)��0��0��cos�Ɓ�1�ɕK��������������A
cos�Ɓ�1�̑���f(cos��)��0�Ccos�Ɓ�0�̑���f(cos��)��0�B
(2)���Ɓ�0 �� ��/2�Ɠ����Ƃ��Acos�Ɓ�1 �� 0�Ɠ����̂ŁA
f(cos��)����S/�݃Ɓ�0�����Ƃ́AS(�ƁCb)�̃ƂɊւ���ő�l�ɂȂ�B
�m��S/��b�n
��S/��b��(�|2b(2�|cos��)�{a)�sin�� (4)
��S/��b��0�Ƃ����ƁA(2)���sin�Ɓ�0������A
b��a/2/(2�|cos��) (5)
0��cos�Ɓ�1����������A
0��a/4��a/2/(2�|cos��)��a/2
�ƂȂ�Ab��a/2/(2�|cos��)��(1)�����B
(4)��b�̌W���|2(2�|cos��)�͕K�������Asin�Ɓ�0�Ȃ̂ŁA
��S/��b��0����b�́AS(�ƁCb)��b�Ɋւ���ő�l�ɂȂ�B
�mS�ő��^����(�ƁCb)�n
(3)�C(4)���A
2b2cos2�Ɓ{b(a�|2b)cos�Ɓ|b2��0 �@
�|2b(2�|cos��)�{a��0 �A
�ł���Ηǂ��B�A��b�ɂ��ĉ�����(5)�A������@�ɑ������A
2cos�Ɓ|1��0
��B�����cos�Ɓ�1/2�C�Ɓ�60���B
���̎�b��a/2/(2�|cos��)��a/3�B���̎���S�́A
| S(��/3�Ca/3) | ��b2cos��sin�Ɓ{b(a�|2b)�sin�� |
| ��a2/9�1/2�31/2/2�{a/3�a/3�31/2/2 | |
��
|
�����D�Ƃ��̗��[����1/3��60���ɐ܂�Ȃ����Ƃ������ʍő�B

| NO.1040 | 2001.9.23. | Junko | �H�v�́i�Q�j |
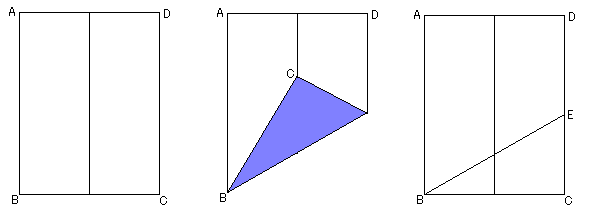
���̐}�̒����`ABCD�ɂ����āAAD=3�AAB=4�Ƃ��܂��B
A��D�AB��C���d�Ȃ�悤�ɔ����ɐ܂�ڂ����܂��B
���̐܂�ڂ�C���d�Ȃ�悤�ɁAB���N�_�ɐ܂�ڂ����čL���܂��B
�O�p�`BCE�ɂ����āA��EBC���R�O���A��BEC���U�O������A
CE:EB:BC��1:2:��3
�]���āAEB��2��3����12
���낢��Ǝv���߂��炷���ŁA
NO.1034�@�����`�̐܂莆�i�T�j���q���g�ɂȂ�܂����B
�u�����A�������I�v���Ďv���u�ԁA���܂łȂ�ŔY��ł����낤�Ǝv���܂��B
����͂����ƈ�ʉ����āA�Q�ӂ̒��������C���̒����`����A�め������肾�������ł��ˁH

| NO.1041 | 2001.9.24. | �n���@�� | �H�v�́i�R�j |
���̉ۑ�͂����ƈ�ʉ��ł���悤�ȋC�����Ă��܂��E�E�E�Ƃ������Ƃł����A
���̑O�ɉ��T�@�c�R�̒����`�����P�T�͔@���ł��傤���H

| NO.1042 | 2001.9.25. | yokodon | �f���̋t���̘a���P�����H |
�͎��V���[�Y4
n �����R���Ƃ���B
����oan�p�̊e���́A�ȉ��̏����ɏ]���Ē�܂���̂Ƃ���B
(i) a1 �� 2
(ii) �e ak�ik �� 1,2,...,n�j�ɑ��A x �Ɋւ���ȉ��̕s���������ŏ��̎�
�R���� an+1 �Ƃ���B
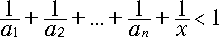
�i1�j���̓��������藧���Ƃ������B
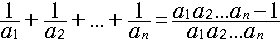
�i2�j�قȂ鎩�R�� k, l �ɑ��Aak �� al �݂͌��ɑf�ł��邱�Ƃ������B

| NO.1043 | 2001.9.27. | Junko | �H�v�́i�S�j |
NO.1040�@�H�v�́i�Q�j�Ɠ��l�ɂ��āACE=��R�܂��B
���̐}�̂悤�ɂ�����Q�{���āACF=�Q��R�A���Ɉڂ����Ƃ�GC=��R
�]���āAGF=��P�T

| NO.1044 | 2001.9.27. | yokodon | �������O�p�`�i�T�j |

NO.1037�@�������O�p�`�i�S�j�ŁA
���̗̈�̋��E�̈ꕔ���������ł��邱�Ƃ��m�F���܂������A
���̏œ_�Ə����͈�̂ǂ��ɂ���̂ł��傤�H�Ƃ����̂��A���܂��Ƃ��čl���Ă݂���
�Ǝv���܂��B
�@�Ƃ����Ă����_�͊ȒP�ŁA���n�`�a�Ɓ��o�p�q�̏d�S�͈�v���A������f�Ƃ�����
�A�f���œ_�ɂȂ��Ă��܂��B�܂������n�f�̒��_���g�Ƃ���ƁA�g��ʂ�ӂ`�a�ɕ�
�s�Ȓ��� m �������ɂȂ��Ă��܂��B
�@���ہANO.1037�@�������O�p�`�i�S�j�̐}-�P�̍��W�n�̂��ƂŁA
�f(0, 2��3/3) �A�g(0, ��3/3) �Ȃ�
�ŁA�_�m (X, Y) �̋O�Ղ� �f�m���m�s�i�A���A�_�s�͂m���璼�� m �ɉ��낵������
�̑��j�����悤�Ɏ��ƁA���̕������̎����o�Ă��܂��B���̂Ƃ��A���������
�_�m���i�ܘ_�A���n�`�a�̓����ɂ����āj��Œ肵�����Őڐ��������ƁA�m������
�p�q�̒��_�ł����Ċ����o�p�q�����O�p�`�ɂȂ�悤�ȂR�_�o�A�p�A�q��ӂ`�a�A
�a�n�A�n�`��Ɏ�邱�Ƃ��o���܂��i�o�͂m�ɂ�����������̖@���ƕӂ`�a�̌�_��
���ċ��߂邱�Ƃ��o���܂��j�B
�@�t�ɁA�i���W����e�ӂ̒����̏�����������Ă��ȉ��͐��藧�͂��ł��j�A�f
��������p�q�ɉ��낵�������̑����m�Ƃ���ƁA�m�͐����p�q�̒��_�ł���A�����
���� m �ɂm���牺�낵�������̑����s�Ƃ���ƁA�f�m���m�s�����藧���Ƃ�����
���Ƃ��o���܂��B�ȏ�́A�x�N�g���⏉���̒m�����g���ďؖ��ł���͂��Ȃ̂�
�A�����̂�����͒��킵�Ă݂Ă͂������ł��傤���H

| NO.1045 | 2001.9.27. | �l�c�@���� | �ő�J�ʁi�R�j |
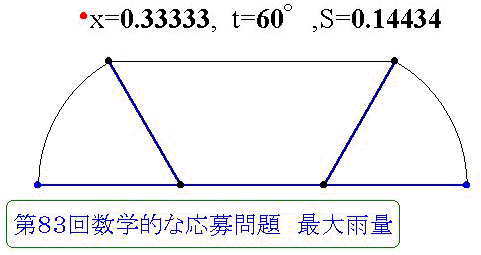
�f�q�`�o�d�r�ɂ��𓊍e���܂��D
�����`�a�̒������P�C�܂�Ȃ��镔���̒����i�`�b�C�a�c�j�����C
�p�i�ڂ`�b�d�C�ڂa�c�e�j�����i�O�������P�^�Q�C�O�������^�Q�j�Ƃ��܂��D
���̂����̒f�ʂł��铙�r��`�̖ʐς����ő�ɂȂ�悤�ɁC���C����I�ׂ悢�D
�@�@�O.�O�O�P�������P�^�Q�C�O.�O�O�P���������X�O��
�͈̔͂ŁC���C���̂����ݒl���C�����C���ꂼ��͈͂̂P�^�P�O�����݂Ŗʐς����v�Z���Ă����C
�ő�ɂȂ�ꍇ�̂��C�������߂܂��D���������ꂼ�ꂕ�C���Ƃ��܂��D
�@����ɁC
�@�@���|�����������{���C���|�����������{��
�Ƃ��C�����ݒl���C�����P�^�P�O�{���C�V���ɍő�ƂȂ邁�C�������߂܂��D
�@���̌v�Z�����v�U��J��Ԃ��C�ő�ƂȂ邁�C�������߂܂��D
�@���̃X�N���v�g�ɂ��C�����ő�ƂȂ�̂́C
�@�@�����O.�R�R�R�R�R�C�����U�O���i�����O.�P�S�S�R�S�j
�̏ꍇ�ł��邱�Ƃ�������܂��D
�@�������C���̃X�N���v�g�͌v�Z���I���̂ɁC�����Ԏ��Ԃ��������Ă��܂��܂��D
���̓s�x�C�v�Z���ʂ�\������悤�ɂ��Ă���̂ŁC����Ȃ�ɉɂԂ��ɂ͂Ȃ�ł��傤���C
�C���Z���l�ɂ͂��������m��܂���D
�`(�O�C�O)�C�a(�P�C�O)�C
�b(���C�O)�C�c(�P�|���C�O)�C
�d(���|��cos���C��sin��)�C�e(�P�|�d���C�d��)
# file://Click�Ōv�Z�J�n # m:=0 # u:=0 # v:=0 # for d:=1 to 6 # if d=1 then # Hx:=.001 # Hy:=1/2 # k:=(Hy-Hx)/10 # Ix:=.001 # Iy:=90 # @:=(Iy-Ix)/10 # else # Hx:=u-k # Hy:=u+k # k:=k/10 # Ix:=v-@ # Iy:=v+@ # @:=@/10 # endif # for a:=Hx to Hy step k # for b:=Ix to Iy step @ # s:=(len(C,D)+len(E,F))*Ey/2 # if m<s then # m:=s # u:=a # v:=b # endif # draw # next # next # next # a:=u # b:=v # draw # ---

 E-mail
E-mail
 �߂�
�߂�