
Weekend Mathematics/コロキウム室/2000.4〜6/NO.94
| NO.806 | 2000.5.3. | 水の流れ | ピタゴラス数(1) |
太郎さんは、有名なピタゴラスの定理(三平方の定理)
x2+y2=z2の自然数解が次のように表されることを
本を読んで知っています。
x=2mn、y=m2−n2、z=m2+n2
(ただし、m、nは互いに素で、m>nとする)
そこで、ピタゴラスの定理を満たす3つの自然数の組をピタゴラス数と言います。
ちなみに、
| (x,y,z)= | (3,4.5),(5,12,13),(7,24,25),(8,15,17),(9,40,41), |
| (11,60,61),(12,35,37),(13,84,85),(16,63,65),(20,21,29), | |
| (20,99,101),(28,45,53),(33,56,65),(36,77,85),(39,80,89), | |
| (48,55,73),(60,91,109),(65,72,97),・・・・・・ 、ここで、問題です。 |
問題1:
x2+y2=z2の自然数解
x=2mn、y=m2−n2、z=m2+n2
をどのようにして導いてあるのか。
(ただし、m、nは互いに素で、m>nとする)
問題2:
x2+y2=z2の自然数解の表現は上記以外、他にもあるのか。
問題3:
ピタゴラス数の3つの自然数の積が60の倍数であること示してください。
質問:
ピタゴラス数の3つの自然数に関して、何か共通して言えていることがあれば、教えてください。

| NO.807 | 2000.5.3. | Junko | ピタゴラス数(2) |
NO.806 ピタゴラス数(1)の問題2
について、3.「らせん階段の問題」のコメントで書いた内容を再び書きます。
ところで、「X2+Y2=Z2」 を満たす整数X、Y、Zの組(ピタゴラス数といいます。)は一体どの位あるのでしょうか。 結論からいうと無数に存在します。 「32+42=52」は あまりにも有名だからご存じですよね?
1組見つかるとその整数倍「62+82=102」、 「92+122=152」・・・を考えただけでも 無数にありますよね。 しかし、これを除いたとしても無数に存在します。次にその探し方を紹介しましょう。
(n+1)2-n2=2n+1という恒等式を利用します。 これより、隣合った整数(n+1とn)の平方の差は必ず奇数(2n+1)になります。 しかも、nを大きくするにつれだんだんと大きくなっていきます。 そこで、奇数かつ平方数(何か整数の2乗)を拾い出せばいいわけです。n 2n+1 4 9=32 「32+42=52」 12 25=52 「52+122=132」 24 49=72 「72+242=252」 40 81=92 「92+402=412」 60 121=112 「112+602=612」 ・ ・ ・というわけでいくらでも見つけることができるのです。

| NO.808 | 2000.5.11. | 水の流れ | 逆関数(1) |
太郎さんは、こんな逆関数の質問を受けましたので、
コロキウム室の愛読者の皆さんにも考えてもらいたく 投稿します。
【Q 次の関数の逆関数を求める。f(x)=SIN(SIN X)】

| NO.809 | 2000.5.13. | 数楽家Crane | 逆関数(2) |
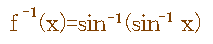 と表現するしかないのかな。
と表現するしかないのかな。

| NO.810 | 2000.5.21. | 水の流れ | ルース=アーロン・ペア |
太郎さんは、今日の朝日新聞の読書欄を読んでいて、興味ある数学本の紹介がありました。
ここの記事からの問題です。
1974年、ハンク・アーロンは715本のホームランを飛ばし、
35年にベーブ・ルースが作った通産714本の記録を破った。
この714と715という数字には不思議な性質がある。
714の素因数の和は715の素因数の和に等しい。
このように、連続する整数で、双方の素因数の和が等しい数のペアを「ルース=アーロン・ペア」
と呼ぶ。
ここで、太郎さんは、他にもこのようなペアがあるように思えてきました。ここで、問題です。
問題1:
714の素因数の和は715の素因数の和に等しいことを示してください。
問題2:
「ルース=アーロン・ペア」を小さい自然数順に、数個発見してください。
問題3:
「ルース=アーロン・ペア」に何か規則性があるか、ないか調べてください。
問題4:
「ルース=アーロン・ペア」は無数にあると、ポール・エルデシュは本に書いています。
無数に存在する証明はできるのでしょうか。
<出典:5月21日朝日新聞の記事にある「放浪の天才数学者エルデシュ」(草思社)から>

| NO.811 | 2000.5.21. | 数楽家Crane | ボールの問題の発展 |
11、「ボールの問題」の発展です。
重いか軽いかわかっている時には、天秤n回で3n個までですが、
重いか軽いかわかっていない時には天秤n回で何個まで判定できるでしょう。

| NO.812 | 2000.5.22. | 水の流れ | 有限小数と無限小数(1) |
太郎さんは、今授業で、Nを自然数としたとき、逆数1/Nが有限小数か無限小数かのを
見分ける方法を宿題にしてあります。理由も考えてください。
次ぎに、Nを自然数とするとき、分数3/Nが、
ちょうど小数第3位までの有限小数となるようなNを求めてください。

| NO.813 | 2000.5.27. | 月の光 | 円錐(1) |
紙に円を描き切り抜きます。次にその円を扇形に切り、内側の角度をθ
とします。
切り口を繋ぐと円錐になり、横から見ると二等辺三角形になります。
円錐の頂点を横から見た時の角度をφとするとき、θとφの関係はどう
なっているでしょうか。

| NO.814 | 2000.5.27. | 月の光 | マッチ棒の直角三角形(1) |
マッチ棒で3辺が5,12,13本の直角三角形を作ります。
この三角形を10本のマッチ棒で3つの面積が等しい部分に分けて下さい。

 E-mail
E-mail
 戻る
戻る