Weekend Mathematics／問題／問題3

３．らせん階段の問題

栄子さんの住んでいる団地には非常階段があります。 その階段はらせん階段で、時々利用しますが、 ５階までとっても長くて大変です。 そこでいったいどの位歩いているのだろうかと 考えてみました。

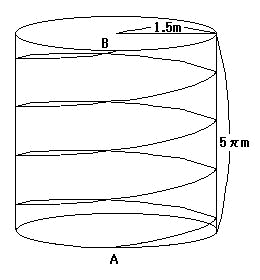
半径１．５ｍ、高さ５πｍの円柱があります。 その円柱には図のようにＡ点からＢ点（Ｂ点はＡ点の真上にある。） までらせん状に４周するひもがあります。 さて、そのひもの全長は何ｍでしょうか？


答えと解説












答えと解説

３．らせん階段の問題

栄子さんの住んでいる団地には非常階段があります。 その階段はらせん階段で、時々利用しますが、 ５階までとっても長くて大変です。 そこでいったいどの位歩いているのだろうかと 考えてみました。

半径１．５ｍ、高さ５πｍの円柱があります。 その円柱には図のようにＡ点からＢ点（Ｂ点はＡ点の真上にある。） までらせん状に４周するひもがあります。 さて、そのひもの全長は何ｍでしょうか？

回答・その１

４周する時、水平方向の距離は（２π×半径）×４ｍであり、 垂直方向の距離は５πｍである。 従って下図の長方形の対角線が歩いた距離となる。

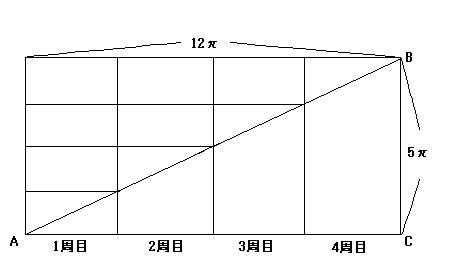
対角線の長さをｌとすれば次の式が成り立つ。

　　　　l=SQR((5π)2+(12π)2)
　　　　　=SQR(25+144)π
　　　　　=SQR(169)π
　　　　　=13π

回答・その２

半径1.5m、高さ５πmの円柱を展開する。 これにらせん状に４周するひもがあるので下の図のようになる。

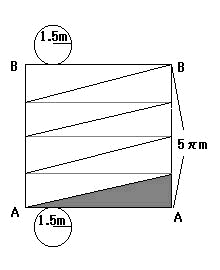
斜線の三角形を取り出す。

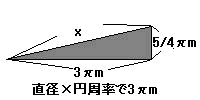
三平方の定理で、
　　　　　x2=(5/4π)2+(3π)2
　　　　　x2=25/16π2+9π2
　　　　　x2=169/16π2
　　　　　
　　　　　x=SQR(169/16)π
　　　　　 =13/4π

これが４つあるので、13/4π×4=13π(m)

あれ−っ？

Ａ−Ｂで切ると、（ひもも一緒に切る。）

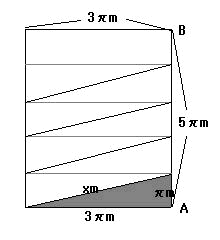
xの長さを求める。 

　　x2=π2+9π2
　　x2=10π2

　　x=SQR(10)π　(m)
　　これが５本だから、5SQR(10)π　(m)

あれ−っ？・コメント

５階まで上るのに階段は５回？

コメント

今回の問題はピタゴラスの定理（三平方の定理）を使うと簡単に解くことができます。
まずはそのピタゴラスの定理です。
下の図のようにＣを直角とする直角三角形があります。
このとき、三辺の長さａ、ｂ、ｃの間に次の関係式が成り立ちます。
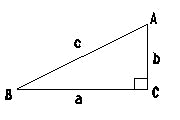ｃ2=a2+b2

この定理は紀元前572年にギリシャの植民地サモス島に生まれたピタゴラス は、タイルで敷き詰められた寺院の床を見て、 この関係に気づいたと伝えられています。
この定理の証明には、３０種類以上の証明法があると言われています。
（収集してみるとおもしろいかも・・・・）
そのうちの２つ紹介します。

証明・その１


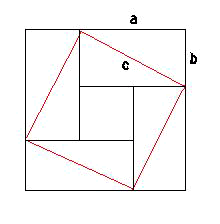
直角をはさむ２辺の長さをａ、ｂ、斜辺の長さをｃとします。 この直角三角形を８つ下の図のように並べると、 内側に正方形ができます。 外側の大きい正方形の面積は(a+b)2で表され、 内側の小さい正方形の面積は(a-b)2で表されます。
図から明らかなように、赤い線で描いた斜線を一辺とする正方形の面積は、 大小２つの正方形の面積のちょうど平均となっています。 したがって、その面積c2は、

　　c2=1/2((a+b)2+(a-b)2)
　　　=a2+b2
であることがわかります。


証明・その２


三角関数が使えるなら、 作図としては斜辺に対して垂線をおろすだけの簡単な証明があります。
∠Cが直角として、頂点Cから対辺ABに垂線を下ろし、垂線の足をHとする。
△CHAと△BHCはともに△BCAと相似であり、 △BCAの面積は△BHCと△CHAの面積の和に等しいが、 相似な多角形の面積は対応する辺の長さの２乗に比例しますから 比例定数をkとすれば、　 

　　　k･ＡＢ2=k･ＢＣ2+k･ＣＡ2

と書くことができ、ＡＢをc、ＢＣをa、ＣＡをbと書けば、
 
       c2=a2+b2

となるわけです。

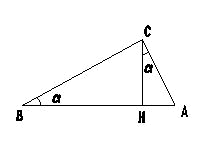
ちなみに∠ACHをαと書けば、 比例定数kは、 

　　　k=1/2sinαcosα=1/4sin2αです。

以上２つの証明は、玉木英彦著「小学生にピタゴラス」みすず書房より。

ところで、「Ｘ2＋Ｙ2＝Ｚ2」 を満たす整数Ｘ、Ｙ、Ｚの組（ピタゴラス数といいます。）は一体どの位あるのでしょうか。 結論からいうと無数に存在します。 「32+42=52」は あまりにも有名だからご存じですよね？
１組見つかるとその整数倍「62+82=102」、 「92+122=152」･･･を考えただけでも 無数にありますよね。 しかし、これを除いたとしても無数に存在します。

次にその探し方を紹介しましょう。 

　　　(n+1)2-n2=2n+1
という恒等式を利用します。 これより、隣合った整数(n+1とn)の平方の差は必ず奇数(2n+1)になります。 しかも、nを大きくするにつれだんだんと大きくなっていきます。 そこで、奇数かつ平方数（何か整数の２乗）を拾い出せばいいわけです。 
　　n　　　2n+1　
　　
　　4　　　9=32　「32+42=52」　　　
　　12　　25=52　「52+122=132」
　　24　　49=72　「72+242=252」
　　40　　81=92　「92+402=412」
　　60　 121=112 「112+602=612」
　　・
　　・
　　・
というわけでいくらでも見つけることができるのです。
　

さて、これによく似た定理に 「フェルマ−の最終定理」というのがあります。
（実は最近ようやく証明がされたところなので、 それまでは「フェルマ−予想」というべきだったのかもしれません。）
フェルマ−の最終定理
ｎが３以上の自然数の場合、
「xn+yn=zn」を 満たす ０でない自然数x、y、zは存在しない。
　赤字部分訂正(2007.9.29.)

フェルマ−は１７世紀のフランス人で、 ツ−ル−ズ地方で法律関係の仕事に従事して生涯を 送った人で、 余暇に数学を研究するのがなによりの楽しみという 変わった趣味（？）の人だったようです。

1637年頃、ギリシャ時代のディオファントスが著した 「算術」という数論の書物を読み、 気づいたことを欄外の余白に書き込んでいった その中にこの定理があったのです。 さらに、「そのことの真に驚くべき証明を見つけたが、 この余白は狭すぎて書けない」と記されていたのです。

以後、たくさんの数学者がこの証明に挑んだけれども成功しませんでした。 ドイツの数学者クンマ−は19世紀中頃に、 100以下の指数nではフェルマ−の定理が成り立つことを含む 一般的な定理を証明しました。 このクンマ−の開発した代数的整数論という理論を深く究める ことによって、1994年の初めにはnが400万以下であれば、 フェルマ−の定理が正しいことがわかるところまできていました。 しかし、たとえ400万でも、１兆でも、すべてではないのです。

そして1994年10月、「すべての場合において」フェルマ−の定理が正しいことが イギリス人アンドリュ−・ワイルズによって証明されたのです。 優秀な若手の数学者が集まって論文を隅から隅までつついてみた結果 「まず間違いはない」と結論し、 最終的には1995年2月、プリンストン大学から出ている雑誌「Annals of Mathematics（数学年報）」 （ワイルズはこれに投稿した。）の編集委員会がワイルズの証明には 間違いがないと結論を下したのです。
かくして、この人騒がせな予想は360年余を経て 最終的に定理となったのです。
（参考：「フェルマ−の大定理が解けた！」足立恒夫著ブル−バックス）

それにしても、n=2の時は無数に存在するのに、 n≧3だと1組も存在しないなんて不思議！！！

問題の出典


秋山仁の中学生おもしろ数学

日本放送出版協会


戻る