Weekend Mathematics乛栤戣乛栤戣35
俁俆丏俁妏偺栤戣

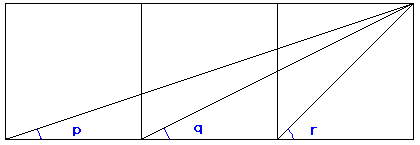
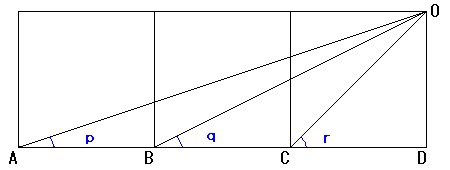
恾偺傛偆偵丄惓曽宍傪俁偮暲傋丄嶰妏宍傪俁偮偐偒傑偡丅
偦偺偲偒丄佢倫亄佢倯亄佢倰丂傪媮傔偰偔偩偝偄丅
乮堦晹夵戣乯
悢妛僷僗儖
壂揷丂峗
拞宱弌斉
乮儁儞僱亅儉丗戞30985崋乯
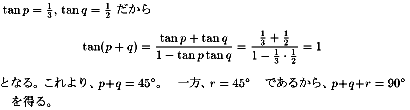

乮儁儞僱亅儉丗儅僒儃亅乯
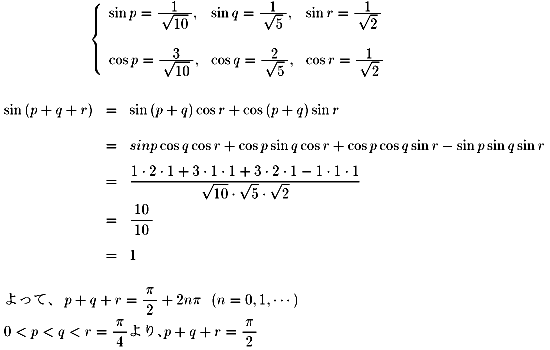

乮儁儞僱亅儉丗彫弔乯
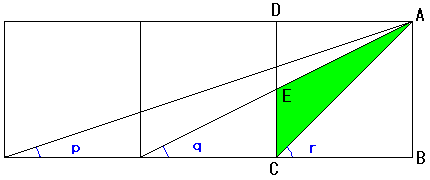
巐妏宍俙俛俠俢傪佢俙俠俛亖佢倰偲側傞傛偆偵偍偔丅
慄暘俠俢偺拞揰傪俤偲偍偔偲丄暯峴慄偺嶖妏傛傝佢倯亖佢俢俙俤偲側傞偐傜丄
埲壓偱佢倫亖佢俤俙俠傪帵偡丅


乮儁儞僱亅儉丗sambaGREEN乯
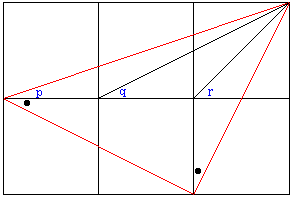
崟揰偺妏偼倯偲摨偠丅愒偄嶰妏宍偼捈妏俀摍曈嶰妏宍丅
偟偨偑偭偰丆倫亄倯亄倰亖係俆亱亄係俆亱亖俋侽亱

乮儁儞僱亅儉丗彮擭俫乯
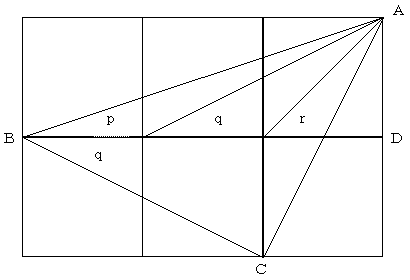
忋恾偵偍偄偰仮俙俛俠偼捈妏擇摍曈嶰妏宍偱偁傞丅
傛偭偰佢倫亄佢倯=係俆搙丄傑偨佢倰=係俆搙偱偁傞偐傜丄
摎偊偼俋侽搙

乮儁儞僱亅儉丗悈偺棳傟乯
俫俤偵懳偡傞俙偺懳徧揰傪俲偲偡傞丅
仮俛俢俤佭仮俲俙俛乮柧傜偐乯
仮俙俢俤佭仮俤俫俲乮柧傜偐乯
| 佢俲俛俤 | 亖侾俉侽亱亅佢俤俛俢亅佢俲俛俙 |
| 亖侾俉侽亱亅佢俛俲俙亅佢俲俛俙 | |
| 亖佢俲俙俛 | |
| 亖俋侽亱 |
| 屘偵丄係俆亱 | 亖佢俛俤俲亖佢俲俤俫亄佢俫俤俛 |
| 亖倫亄倯 |

乮儁儞僱亅儉丗傆偠偗傫乯
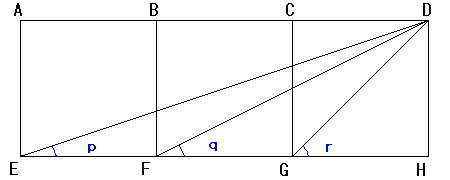
忋偺恾偺傛偆偵丄惓曽宍偺偦傟偧傟偺揰傪
A B C D E F G H
偲偟傑偡丅
偙偙偱暯峴慄偺嶖妏傛傝佢倫亖佢ADE
嶰曈偺斾偑摍偟偄偙偲傛傝仮DFG佷仮EDG
傛偭偰佢倯亖佢EDG
傑偨丄仮DGH偼捈妏擇摍曈嶰妏宍側偺偱佢倰亖佢GDH乮亖45亱乯
亪佢倫亄佢倯亄佢倰亖佢ADE亄佢EDG亄佢GDH亖90亱

乮儁儞僱亅儉丗働僀儞乯
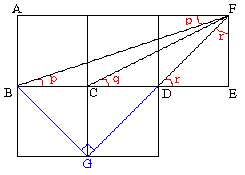
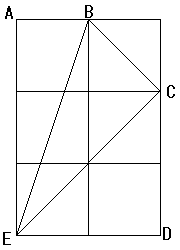
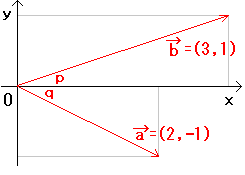
塃恾偺傛偆偵栤戣偺恾宍偵A,B,C,D,E,F偲偆偮偲丄
巐妏宍ABEF偼挿曽宍側偺偱
丂佢AFB亖佢FBE亖倫乮嶖妏乯
仮EDF偼擇摍曈嶰妏宍側偺偱
丂佢EFD亖佢EDF亖倰
偁偲偼佢BFD亖倯偑尵偊偨傜
佢倫亄佢倯亄佢倰亖俋侽並丂
偑惉棫偡傞偺偱 佢BFD亖倯 傪徹柧偟傑偡丅
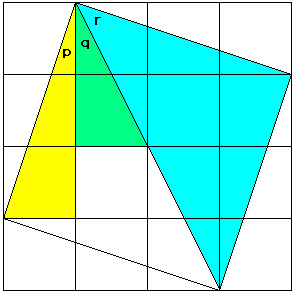
恾偺傛偆偵惓曽宍傪壓偵暲傋偰揰G傪嶌傝丄仮FCE偲仮BFG偵偮偄偰峫偊傞偲
丂CE丗FG亖俀丗俀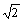 亖侾丗
亖侾丗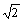 乧嘆
乧嘆
丂FE丗BG亖侾丗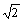 丂丂丂丂丂丂丂乧嘇
丂丂丂丂丂丂丂乧嘇
丂佢CEF亖佢FGB亖俋侽亱丂丂丂丂丂乧嘊
嘆丄嘇丄嘊傛傝擇曈偺斾偲偦偺娫偺妏偑偦傟偧傟摍偟偄偺偱
丂仮FCE佷仮BFG
亪佢FCE亖佢BFD亖倯
亪佢倫亄佢倯亄佢倰亖俋侽亱

乮儁儞僱亅儉丗傆乣乯
傑偢栤戣偺奺捀揰偵婰崋傪晅偗傞
偡傞偲丄偦傟偧傟偺妏偼師偺嶰妏宍偺妏偲偟偰尒傞偙偲偑偱偒丄
偝傜偵丄佢俢乮亖佢俼乯傪嫴傓曈偺挿偝傪斾偱昞偡偲
佢倫 仺 仮俷俙俢 仺 俁丗侾
佢倯 仺 仮俷俛俢 仺 俀丗侾
佢倰 仺 仮俷俠俢 仺 侾丗侾
捈妏傪嫴傓曈偺斾
仮俤俢俠仺侾丗侾
仮俤俠俛仺俀丗侾
仮俤俙俛仺俁丗侾
偟偨偑偭偰丄佢倫亄佢倯亄佢倰亖俋侽並偲側傞丅

乮儁儞僱亅儉丗寧偺岝乯
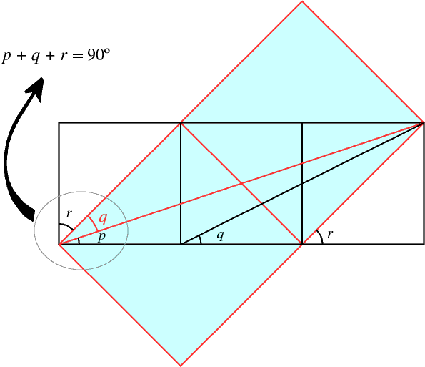
恾傛傝丄佢倫亄佢倯亄佢倰亖俋侽搙

乮儁儞僱亅儉丗戞30985崋乯
恾偵傛傞夝摎丅

乮儁儞僱亅儉丗彫弔乯
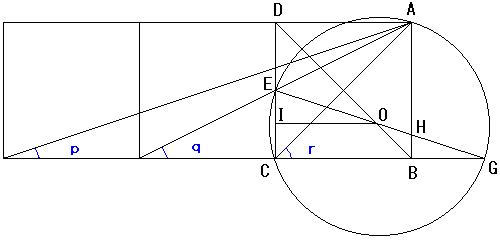
仮俙俤俠偺奜愙墌偺拞怱傪俷偲偟丄俷偐傜曈俤俠偵壓傠偟偨悅慄偺
懌傪丄俬偲偡傞丅
傑偨丄俧傪俤俧偑奜愙墌偺捈宎偲側傞傛偆偵偍偒丄俤俧偲俙俛偺岎揰傪俫偲偡
傞丅
偝傜偵丄佢倫傪帩偮嶰妏宍傪仮p偲偍偔丅
墌廃妏傛傝佢俤俙俠亖佢俤俧俠
傛傝丄偙偙偱偼丄佢倫亖佢俤俙俠傪帵偡偨傔偵仮俤俧俠偲
仮p偑憡帡偱偁傞偙偲傪帵偡丅
俬偼曈俤俠偺拞揰偱偁傞乮俷俬偼俤俠偺悅捈擇摍暘慄)丅
傑偨丄仮俢俬俷偲仮俢俠俛偼憡帡偐傜丄
DI丗IC = DO丗OB = 3丗1丂
偮偓偵丄仮俢俤俷偲仮俛俫俷偐傜丄
DO : OB = DE : BH = 3 : 1
DE = EC 偐傜 EC : BH = 3 :1
仮俤俠俧偲仮俫俛俧偼憡帡偐傜丄
EC : HB = CG : BG = 3 :1
CG = 3BG ,CB = 2EC偐傜
3EC = CG
2EC = DC 偮傑傝丄惓曽宍偺堦曈偱偁傞丅
仮俤俠俧偼幬曈偱偼側偄巆傝偺擇曈偺斾偑3:1偱丄偦偺嫴傓妏偑捈妏偱
偁傞丅
偲偙傠偱丄仮p傪側偑傔偰傒傞偲丄幬曈偱偼側偄巆傝偺擇曈偺斾偑3:1
偱丄偦偺嫴傓妏偑捈妏偱偁傞丅
傛偭偰丄仮俤俠俧偲仮p偼憡帡偱偁傞丅
偮傑傝丄佢倫亖佢俤俙俠偱偁傞偺偱丄
p + q + r = 90 偲傢偐偭偨丅
Q(Junko):
俢俷俛偑堦捈慄忋偵暲傇偺偼丄帺柧偱偼側偄偺偱愢柧偑昁梫偩偲巚偄傑偡偑丒丒丒
A(彫弔):
俢俷俛偑堦捈慄忋偵偁傞偙偲偼丄
嶰妏宍俙俠俤偺奜愙墌偺拞怱偑俷偱嶰妏宍偲奜愙墌偺娭學偐傜丄俙俠偺悅捈擇摍
暘慄忋偵俷偑偁傝傑偡丅
傑偨丄俙俠偼惓曽宍俙俢俠俛偺懳妏慄偱偡偺偱丄俙俠偲俛俢偼屳偄偺拞揰偱悅捈
偵傑偠傢傝傑偡丅
傛偭偰丄俢俷俛偼堦捈慄忋偵偁傝傑偡丅

乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
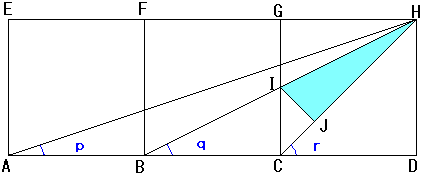
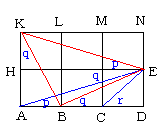
佢倫丄佢倯丄佢倰傪恾偺捀揰俫偵廤傔傞丅
佢倯亖佢俤俫俛乮暯峴慄偺嶖妏乯
佢倰亖佢俠俫俢乮仮俠俢俫偼捈妏擇摍曈嶰妏宍乯
佢倫亖佢俬俫俠
側偤側傜丄俛俫偲俧俠偺岎揰俬偐傜俠俫傊偺悅慄傪俬俰偲偡傞偲
丂丂丂丂丂仮俙俢俫 佷 仮俫俰俬
側偤側傜丄惓曽宍偺侾曈偺挿偝傪侾偲偡傞偲丄
仮俰俬俠偼捈妏擇摍曈嶰妏宍側偺偱
| 俫俰丗俰俬 | 亖乮俠俫亅俠俰乯丗俰俬 |
亖乮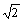 亅 亅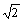 乛係乯
丗 乛係乯
丗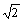 乛係 乛係
| |
亖俁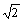 乛係丗 乛係丗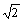 乛係 乛係
| |
| 亖俁丗侾 | |
| 亖俙俢丗俢俫 |
廬偭偰丄丂佢倫亄佢倯亄佢倰亖俋侽並

乮儁儞僱亅儉丗寧偺岝乯
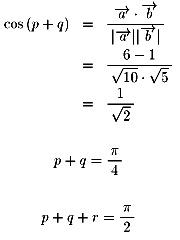

乮儁儞僱亅儉丗寧偺岝乯
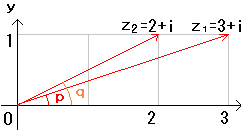
r=兾/4
p=arg z1
q=arg z2
| p+q | =arg(z12) |
| =arg 5(1+i) | |
| =兾/4 |

| kiyo | ch3cooh | 傆偠偗傫 |
| sambaGREEN | 偐偵 | 彮擭俫 |
| Idaho Potato | 彫弔 | toki |
| 悈偺棳傟 | 儅僒儃乕 | 戞30985崋 |
| 傆乣 | 働僀儞 | 寧偺岝 |
| 偪傖傔 | 栭傆偐偟偺偮傜偄偍偠偝傫 |

巹帺恎丄偙傫側偵偨偔偝傫偺夝朄偑偁傞偲偼巚偄傑偣傫偱偟偨丅
嬃偄偰偄傑偡丅傑偩傑偩偁傞偐傕偟傟傑偣傫偹丒丒丒丠
偍傂偲傝偱俁偮傕係偮傕夝朄傪婑偣偰偄偨偩偄偨曽傕偄傜偭偟傖偄傑偡丅
戙昞揑側偲偙傠傪傂偲偲偍傝徯夘偟偰偁傝傑偡丅
偁傞栤戣傪夝偔偺偵偨偔偝傫偺夝朄偑偁偭偰丄
偦傟傜傪尒斾傋傞偺偑巹偼戝岲偒偱偡丅
侾偮偺嶳傪偄傠偄傠側妏搙偐傜挱傔丄偦傟傪搊傞傛偆偵巚偄傑偡丅
偦傟傜傪傒偰偄傞偆偪偵栤戣偺摎偊乮嶳偺捀忋乯偑摉慠偁傞傋偒傕偺偵尒偊偰偔傞偺
偱偡丅
夝摎丒偦偺侾偺傛偆偵帩偭偰偄偔偲丄
tangent偺壛朄掕棟偺墘廗栤戣偲偟偰嵟揔両偲巚偄傑偟偨丅
堦曽丄夝摎丒偦偺係丄
夝摎丒偦偺俆偺傛偆偵
捈妏擇摍曈嶰妏宍傪嶌傞夝朄傕巹帺恎偲偟偰偼婥偵擖偭偰偄傑偡丅
傓偢偐偟偄抦幆傪帩偪弌偝側偔偰傕丄傄偨偭偲弌傞偲偙傠偑旤偟偄両丂
偲巚偭偰偟傑偄傑偡丅
偙傟側傜彫妛惗偱傕棟夝偱偒傑偡丅
偙偺捈妏擇摍曈嶰妏宍傕挱傔傟偽挱傔傞傎偳丄
乽昁慠乿偵巚偊偰偔傞(?)偐傜晄巚媍偱偡丅
偙傟偵偮偄偰乽Idaho Potato乿偝傫偐傜師偺傛偆側搳峞傪偄偨偩偒傑偟偨丅
偙偺栤戣偺乽椶戣乿偑嶌傟側偄傕偺偐偲峫偊偰傒傑偟偨丅
梫偡傞偵丄tan(p), tan(q) 偑娙扨側暘悢偱丄偐偮丄 tan( p + q ) = 1 傪枮偨偡 傛偆側妏 p, q 偺慻傪尒偮偗傛偆丄偲偄偆偙偲偱偡丅
偲側傝傑偡丅偙偙偱 (m,n) = (1,2) 偲偡傞偲丄崱寧偺栤戣偵側傝傑偡丅
傕偭偲傕丄偙偺娭學幃偼丄 (n+m)亊n 偺奿巕偵捈妏擇摍曈嶰妏宍偑 偼傑偭偰偄傞恾傪昤偄偰傒傟偽柧傜偐偱偡偹丅
偦偙偱丄 m, n 偵彫偝側帺慠悢傪弴偵戙擖偟偰偄偔偲丄
偲偄偆傛偆偵丄偄偔傜偱傕婡夿揑偵夝偺慻傪惗惉偱偒傞偙偲偵側傝傑偡丅
偱傕丄偺傛偆偵乽旤偟偄乿栤戣偵側傞傕偺偼丄巆擮側偑傜丄 傎偐偵偼尒偮偐傝偦偆偵偁傝傑偣傫丅
tangent 偱偼側偔丄媡悢傪偲偭偰 cotangent 偱峫偊傞偲丄
偲側傝傑偡偑丄偪傚偆偳丄 ( cot(p), cot(q) ) = ( 2, 3 ) 偑丄 偙偺曽掱幃偺(懳徧惈傪彍偄偰)桞堦偺帺慠悢夝偵側偭偰偄傑偡丅
偦偆偄偆堄枴偱丄寢嬊丄
傪梡偄偰嶌偭偨栤戣偑乽嵟椙乿偲偄偆偙偲偵側傞傛偆偱偡丅
偄偨偩偄偨夝朄偺拞偱巹偑堦斣姶摦偟偨偺偼丄
夝摎丒偦偺侾侽偲夝摎丒偦偺侾侾偱偡丅
偳偪傜傕丄堦晹奼戝亄夞揮偝偣傞偙偲偱帇妎揑偵摎偊傪帵偟偰偄傑偡丅
愢柧偼偄傜側偄丄恾傪尒偰傕傜偊傟偽廩暘丄偲偄偆姶偠偱偡丅
奆偝傫偐傜婑偣傜傟偨夝摎傪尒偣偰偄偨偩偄偰丄堦斣妝偟偐偭偨偺偼巹偐傕偟傟傑偣傫丅
偙偺嶳傪搊傞偺偵偄傠偄傠婑傝摴傪偟偨傝丄彫摴偵擖偭偨傝偟側偑傜妝偟傑偣偰偄偨偩偒傑偟偨丅
夋憸傗恾丄TeX file側偳丄帪娫傪偐偗偰夝摎偟偰偄偨偩偒姶幱偟偰偍傝傑偡丅
 E-mail
E-mail
 栠傞
栠傞