
Weekend Mathematics/コロキウム室/1999.4〜6/NO.61
| NO.516 | '99 6/5 | Junko | 連続の証明(4) |
「ε-δ(イプシロン−デルタ)論法」というのを紹介します。
(極限をきちんととらえようとするとき、
避けては通れないのですよね。)

εによって、どんなに小さい区間を与えられたとしても、
それなりに(εにdependした形で)区間(a-δ,a+δ)をとってくれば、
その区間内にあるxに対するf(x)の値を、(α-ε,α+ε)内に納めることができる、
ということです。

| NO.517 | '99 6/5 | Junko | ロシア農民の掛け算 |
本屋さんで、別冊Newton「自然にひそむ数のミステリ−」(Newton Press \2040)
というのを見つけました。
数学をテ−マにしたものははじめてだそうで、以外な感じがしないでもありません。
 その中に、「ロシア農民の掛け算」というのが紹介されています。
その中に、「ロシア農民の掛け算」というのが紹介されています。
(以下、上記の本からの引用です。)
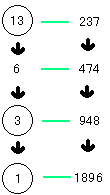
たとえば、13×237の場合、13を2で割った答を下へ下へと書いていく (余りは無視する)。 答が1になるまで続ける。 このときに答が奇数になったものをマ−クしておく。 次に13の横に同じようにして、237を2倍、さらにその2倍した数を、 下へ下へと同じ行数だけ書いていく。 最後に、マ−クした答えに対応する237の列の答えを合計する。 それが掛け算の答である。
13×237 = 237+948+1896 = 3081
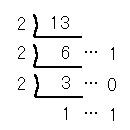 2で割っていくという操作は、13の2進法表示を求めるときの操作そのものです。
奇数をマ−クするというのは、2進法表示で「1」となる場所を求めることになります。
(奇数だと2で割った時に余りが1になりますからね。実際には1つづつずれますが・・・。)
2で割っていくという操作は、13の2進法表示を求めるときの操作そのものです。
奇数をマ−クするというのは、2進法表示で「1」となる場所を求めることになります。
(奇数だと2で割った時に余りが1になりますからね。実際には1つづつずれますが・・・。)
13の2進法表示は、13=1101(2)となります。
| 13×237 | |
| = | (23×1+22×1+21×0+20×1)×237 |
| = | (23×237)×1+(22×237)×1+(21×237)×0+(20×237)×1 |
| = | 1896×1+948×1+474×0+237×1 |
ここで、「×1」は残す、「×0」は要らないということになります。
奇数のところだけ(2進法表示をしたときに1になるところだけ)足していった所以です。
掛け算ですからどうかけてもいいのでしょうが、13の方は半分、半分とスリムになっていく分、
237の方に押しつけているようで、おもしろいなあと思います。

| NO.518 | '99 6/5 | Weadore | 長方形の5等分 |
定規だけを用いて長方形を5等分せよ。

| NO.519 | '99 6/6 | 月の光 | 高貴な未解決問題(2) |
1.第n番目の素数Pnをnで表せたらどんなに素晴らしいことでしょう?
について、F(j)を
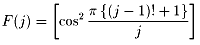
と定義します。([ ] はガウス記号)
ウィルソンの定理”(p-1)!+1がpで割り切れるときに限りpは素数である”から
F(j)はjが素数のとき1、合成数のとき0となります。
例えば
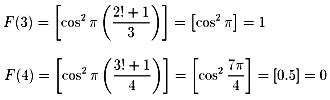
これを使うと素数計算関数π(n)は
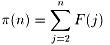
で表され、n番目の素数Pnは次の威圧的な式で表されます。
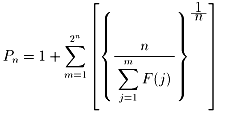
上のπ(n)の式を使うと
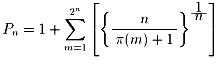
お分かりのようにこの式は有用ではありません。
わずか三番目の素数5を計算するだけでもとても多くの計算が必要です。
もっと簡単な式はないのでしょうか。
Pnの推定値であれば素数定理から次のことが示されます。
Pn〜nlogn+n{log(logn)−1}
=でないのが残念ですがこれだけでもおもしろいと思います。
いくつか値を挙げてみます。
| n | 推定されたPn | 実際のPn | パーセント誤差 |
|---|---|---|---|
| 500 | 3521 | 3571 | 1.40 |
| 1000 | 7840 | 7919 | 1.00 |
| 2000 | 12454 | 12553 | 0.75 |
| 3000 | 27260 | 27449 | 0.69 |
| 4000 | 37638 | 37813 | 0.46 |
| 5000 | 48296 | 48611 | 0.65 |
ここで、junko先生が「数学の宇宙」のなかで初めに読まれた
「素数定理」とは、
素数定理:nより小さい素数の数はnをnの対数で割った近似である。
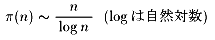
のことです。
これは1792年、15歳のガウスによって推測され、
1896年に2人の数学者
ジャック・アダマールとデ・ラ・ヴァレー・プーサンによって独立に
証明されました。
では、n/lognはどれほどπ(n)の近似となるのでしょうか。
あとで表を書きますが、
不幸にして、パーセント誤差は緩やかに減少します。
もっと正確な別の式は存在しないのでしょうか。
あります!
「nの対数積分」と呼ばれ、ガウスにより発見されました。
li(n)として示されます。
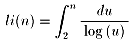
この積分を直接実行するのは大変なので、次の級数で近似すると便利です。
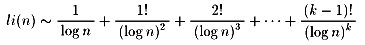
kはli(n)を近似するために級数の中で一緒に加える項の数です。
この式はnとkがかなり大きいときには非常に正確です。
下の表ではk=12まで取って近似の値を出しています。
| n | π(n) | li(n) | n/logn | パーセント誤差 ( li(n)/ n/logn) |
|---|---|---|---|---|
| 102 | 25 | 111 | 21 | 344/16.00 |
| 105 | 9,563 | 9,630 | 8,635 | 0.385698/9.47 |
| 1010 | 455,052,512 | 455,055,600 | 434,294,493 | 0.000678/4.56 |
| 1013 | 346,065,536,839 | 346,065,632,227 | 334,072,662,679 | 0.000027/3.47 |
| 1015 | 29,844,570,422,669 | 29,844,571,135,055 | 28,952,965,081,228 | 0.000002/2.99 |
この表を見ていると、D(n)=π(n)− li(n)は常に増加するように
見えますが、1914年、ジョン・リトルウッドは
D(n)は十分大きなnに対して減少するだけでなく、
負になり、正と負の間の符号を無限回変えることを
証明しました。
そしてドイツの数学者リーマンは li(n)を改良した
関数 R(n)を構築しました。
まだまだ話題はありますが、長くなったので終わりにします。
<参考文献:数学の不思議−数の意味と美しさ−(青土社)>

| NO.520 | '99 6/6 | 月の光 | 「数学の宇宙」(2) |
今回僕が参考にした本「数学の不思議」(青土社)も似た内容ですが
好きな本の内の1つです。
素数定理のもう少し詳しい内容と、リーマン予想に関すること、
インドの天才数学者ラマヌジャンの発見した驚くべき式などが書かれています。
こちらもお勧めの本です。
NO.268連分数その2の問題もここから出しました。

| NO.521 | '99 6/6 | 月の光 | 高貴な未解決問題(3) |
2.与えられた素数の、次の素数を発見できたら?
与えられた素数の次の素数は近似的にどこにあるのでしょうか。
1845年、ジョセフ・ベルトランが、2≦nなら
nと2nの間には少なくとも一つの素数が存在すると推測し、チェビシェフにより証明されました。
しかしこれでは大した助けにはなりません。Pnとそれの後に続くものに対する
関係としてあと二つあります。
Pn+Pn+1>Pn+2 と
Pm・Pn>Pm+nです。
では、与えられた素数の次の素数を求める式とはどんなものでしょうか。
それは、F(j)をπ(n)を表すときに定義した関数、PnをPとし、
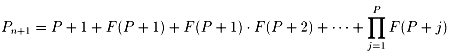
で表されます。これも有用ではありません。
理想的にはn番目の素数Pnや、
与えられた素数の次の素数を求める単純な式があればいいのですが、
そのような式はまだ存在しないそうです。
いつかそのような単純な式が見られる日が来るのでしょうか。
<参考文献:数学の不思議−数の意味と美しさ−(青土社)>
素数に関してここに詳しく(英語で)書かれています。
The Prime Pages
How Many Primes Are There?

| NO.522 | '99 6/7 | 水の流れ | エジプト人のかけ算・わり算 |
NO.517 「ロシヤ農民のかけ算」 で思い出しましたので、今度はエジプト人のかけ算・わり算 のお知らせします。
エジプト人は2倍と1/2だけの計算で、すべてのかけ算・わり算を行います。 例えば
13×237 1* 237 2 474 4* 948 8* 1896左側に、1,2,4,8,16、32,・・・・ と上の数字の2倍を書いていく。
次に、わり算です。
39÷8 1 8 2 16 4 32* 1/2 4* 1/4 2* 1/8 1*左側に、8の1倍、2倍、4倍、・・・ で39に近い数字まで続ける。
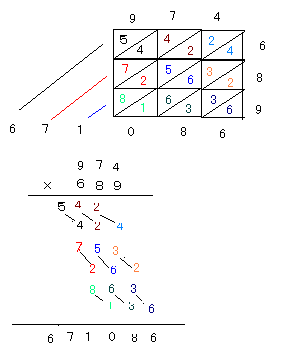
次に、中世のヨーロッパで流行した格子かけ算をご紹介します。
例えば、974×689 を右図に示します。
最後は、右から順に斜めに足してください。
積み算も図に示します。
現在、私達が行っているかけ算での誤算の大部分は、途中の繰り上がりの
数字を暗算で加えるところにあります。
この格子かけ算は途中の暗算が全くふくまれていないので、
精神的疲労がなく、極めて効率的である。
また、この方法は頭からかけていくので、
自分の必要とする位まで最小限の労力で求められるという便利さもある。
<参考文献:「数の世界雑学辞典」(日本実業出版)方野善一郎 著 >

| NO.523 | '99 6/7 | プ−太 | 連続の証明(5) |
NO.516 連続の証明(4)でjunkoさんが、
連続や極限の定義を厳密のおこなう為にεーδ論法
をあげていましたが、別な方法もあることを紹介します。
実数列の極限


| NO.524 | '99 6/7 | Junko | 連続の証明(6) |
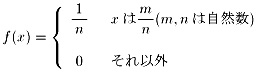
とする。
xが無理数のとき、f(x)が連続であることを証明せよ。
これをεーδ論法で証明してみます。


| NO.525 | '99 6/7 | Junko | バーレーボールの得点(2) |
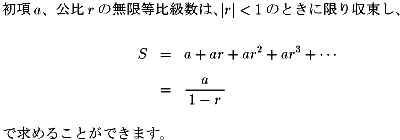
1.Aがあっさり1点とればいいわけですが、たとえBサ−ブ権をとられたとしても、
また取り返して、得点すればいいわけです。
そう考えると、次のような無限等比級数になります。
Aにサ−ブ権がある状態で、Aが1点をとる確率をP(A,A)とします。
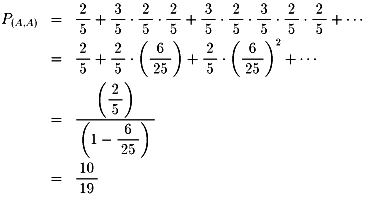
2.

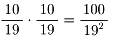
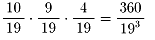
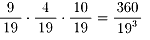
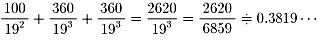

 E-mail
E-mail
 戻る
戻る