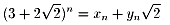なる(ｘｎ，ｙｎ)が、
方程式ｘ２＝２ｙ２＋１ の解であることを
数学的帰納法で示します。Weekend Mathematics／コロキウム室／1999.7〜9／NO.67
| NO.575 | '99 7/13 | Junko | 三角数は平方数？（３） |
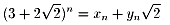なる(ｘｎ，ｙｎ)が、
方程式ｘ２＝２ｙ２＋１ の解であることを
数学的帰納法で示します。
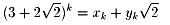に対して、
ｘｋ２＝２ｙｋ２＋１ とする。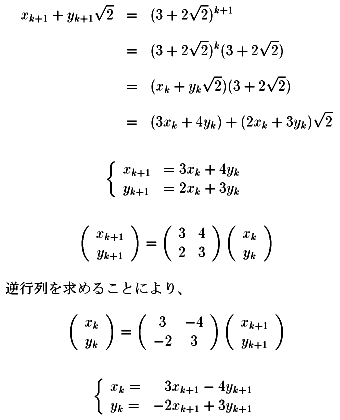
これを、ｘｋ２＝２ｙｋ２＋１ に代入する
ことにより、ｘｋ＋１２＝２ｙｋ＋１２＋１ を
得ますから、
数学的帰納法により証明されます。
しかしながら、これは
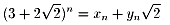なる(ｘｎ，ｙｎ)が、
方程式ｘ２＝２ｙ２＋１ の解であることを
示したにすぎず、方程式ｘ２＝２ｙ２＋１ を解いたことにはなりません。
「方程式を解く」というのは、それを満たす解を”すべて”求めることだからです。
| NO.576 | '99 7/15 | ものもの | フェルマ−の大定理 （５） |
Ａn＋Ｂn＋・・・＝Ｚn
（Ａ,Ｂ,・・・,Ｚ≠０）（nは自然数）
左辺の項数をＭ（≧２）とすると
| NO.577 | '99 7/15 | Junko | 三角数は平方数？（４） |
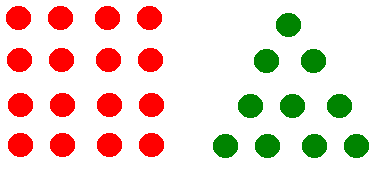
一辺ａの正方形のおはじき個数は
一方、一辺ｂの正三角形のおはじきの個数は、
１＋２＋３＋・・・＋ｂ＝1/2・ｂ（ｂ＋１）
これが等しければいいので、
1/2・ｂ（ｂ＋１）＝ａ２
ｂ（ｂ＋１）＝２ａ２
左辺を平方完成すると、
（ｂ＋1/2）２−1/4＝２ａ２なので、
ｂ＋1/2＝ｃとおく。
そうすると、ｃ２−1/4＝２ａ２ となり、
４ｃ２−１＝８ａ２
（２ｃ）２＝２（２ａ）２＋１ となる。
さらにここで、２ｃ＝ｘ、２ａ＝ｙとすれば、
となり、ペルの方程式に帰着される。
ここで、ａ，ｂは正のの整数なので、ｘ＝２ｂ＋１，ｙ＝２ａも正の整数である。
NO.572で「kiyo」さんが、示してくださった解をあてはめてみます。
ｘ＝３、ｙ＝２のとき、ａ＝1/2・ｙ、ｂ＝1/2（ｘ-1）より、ａ＝1、ｂ＝1。
このとき、おはじきの個数は１個。
ｘ＝１７、ｙ＝１２のとき、ａ＝６、ｂ＝８。このとき、おはじきの個数は３６。
ｘ＝９９、ｙ＝７０のとき、ａ＝３５ｂ＝４９。このとき、おはじきの個数は１２２５。
・・・
| NO.578 | '99 7/15 | 数楽者 | スターウォーズグッツ（２） |
最初に１個買うと１つ手に入ります。
２個目は、自分がすでに持っているものと違うグッズが
得られる確率が49/50なので、２個目を手に入れるまでの
期待購入数は50/49となります。
同様に、３個目を手に入れるまでの期待購入数は50/48
・・・
４９個目を手に入れるまでの期待購入数は50/２
最後の１個を手に入れるまでの期待購入数は50/１
したがって、すべてを手に入れるまでの期待購入数は
50(1/1+1/2+1/3+・・・+1/49+1/50)
となります。
期待購入数／グッズの総数＝1/1+1/2+1/3+・・・+1/49+1/50
となり、どこかで見かけた式が出てきました。
| NO.579 | '99 7/17 | Junko | 三角数は平方数？（５） |
一般の「ペルの方程式： Ｘ２＝ｋ・ｙ２＋１」・・・(*)
について考えてみます。
これを満たす解が１組みつかったとしたら(存在する保証はどこにもないのですが・・・)
これを、
ｘ1＝ａ、ｙ1＝ｂとして、
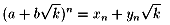なる（ｘｎ , ｙｎ）を考えます。
これもやはり方程式（*）の解になることが>NO.575と
同様に数学的帰納法で証明されます。
| NO.580 | '99 7/17 | Junko | スターウォーズグッツ（３） |
実際に次の式を「mathematica」に計算してもらいました。
| 50(1+1/2+1/3+1/4+･･･+1/50) | |
| = | (13943237577224054960759/61980890084919934128) |
| = | 224.96 |
| NO.581 | '99 7/17 | Junko | オイラーの「無限解析入門（１）」（２４） |
ｆ（ｘ）＝１÷（１−ｘ）（１−ｘ２）（１−ｘ３）
（１−ｘ４）（１−ｘ５）（１−ｘ６）
（１−ｘ７）（１−ｘ８）（１−ｘ９）
（１−ｘ１０）・・・とする。
この分母を
Ｆ（ｘ）＝（１−ｘ）（１−ｘ２）（１−ｘ３）
（１−ｘ４）（１−ｘ５）（１−ｘ６）
（１−ｘ７）（１−ｘ８）（１−ｘ９）
（１−ｘ１０）・・・
とおいて、計算せよというのがNO.561の宿題でした。
これはちょっと大変・・・ということで、「mathematica」の登場です。
（１−ｘ３０）までを展開しました。
Ｆ（ｘ）＝（１−ｘ）（１−ｘ２）（１−ｘ３）
（１−ｘ４）・・・（１−ｘ３０）
＝１−ｘ−ｘ２＋ｘ５＋ｘ７−ｘ１２−ｘ１５＋ｘ２２
＋ｘ２６＋ｘ３１・・・＋ｘ４６５
ｘ３０までの係数は正確なものですから、
Ｆ（ｘ）＝１−ｘ−ｘ２＋ｘ５＋ｘ７−ｘ１２−ｘ１５＋ｘ２２
＋ｘ２６＋・・・
規則性が見え隠れします。
| NO.582 | '99 7/18 | 水の流れ | オイラーの「無限解析入門（１）」（２５） |
オイラーの無限解析入門（１）の第１３夜の始まり、始まり。
オイラーの三角形のＳ（ｍ）の数列を並べてみましょう。
１，２，３，５，７，１１，１５，２２，３０，４２，・・・
この数列の規則性を見つけるのが目的です。
そのために、母関数を持ち出してきています。
| Ｆ（ｘ） | ＝（１−ｘ）（１−ｘ２）（１−ｘ３） （１−ｘ４）・・・（１−ｘ３０） |
| ＝１−ｘ−ｘ２＋ｘ５＋ｘ７−ｘ１２−ｘ１５＋ｘ２２ ＋ｘ２６−・・・ | |
| ＝１−ｘ（１＋ｘ）＋ｘ５（１＋ｘ２）−ｘ１２（１＋ｘ３）＋ｘ２２ （１＋ｘ４）−・・・ |
| NO.583 | '99 7/19 | 水の流れ | スターウォーズグッツ（４） |
太郎さんは、この夏休みに「スターウォーズ３部」を観に行く予定です。
某飲料水メーカーは、スターウォーズグッツをＡかＢの２タイプの
おまけのうちどちらかに入れて、販売を始めました。
各タイプごとにｎ種類の異なるおまけがある。
このおまけグッツは２タイプすべての種類がランダムに当確率に出回っています。
ＡかＢのどちらかの全種類が集まるまで、１回に１本ずつ買うことにする。
太郎さんは、ＡかＢのどちらかの全種類が集まるまでに飲料水を買う
本数の平均が気になりました。ここで、問題です。
問題１：
ｎ＝３として、具体的に、買わなければならない本数の平均Ｅを求めよ。
問題２：
一般に、ｎ種類の場合の平均本数を求めよ。
皆さん、考えてください。
太郎さんも童心にかえって、飲料水を買ってきては集め始めましたが、
なかなかうまく集まりません。皆さんも、考えてください。
| NO.584 | '99 7/19 | spooky | オイラーの「無限解析入門（１）」（２４） |
さきほど、NO.546を読んだのですが、
２×３×５×７×１１×・・・＝1/４π2
の証明については、少し疑問が あります。
たしかにオイラーの時代ならよかった（？）のかもしれませんが・・・・。
それは、解析接続に関してです。
たとえば、ζ（ｓ）は確かに複素平面全域に解析接続できます。
詳しいことは私も証明がいまいち理解できていないのでいえませんが、
すこし参考書 を参考に書いてみます。
だから、１＋２＋３＋４＋・・・・の和というのは、
実際には収束しないのですが、 これがζ（-1）であると考えると、
上の式より値が出てきてしまうのです。
しかし、ζ（−１）というのはすべての自然数の和とは違うわけです。
昔はこのような区別が付いていなかったため、
オイラーはこのように書いたのでしょう。
つまり、すべての自然数の積というのも、
Γ（ｓ）のｓ→∞の極限とかそういうもの なのかもしれません。
ただ、それがすべての自然数の積であるとは思わない方がいいと思います。
あくまでも、関数の解析接続したものを考えているわけですから。
Γ関数がいくら階乗の拡張だといっても、Γ（１／２）＝（−１／２）！
とは考えないでしょう？？
いわゆるオイラーの公式も実関数の立場（オイラーの立場）では
テイラー展開に複素数を代入するという、無茶な代入をしなければなりません。
本来ならば、複素関数として３つを定義して考えなければならないわけです。
ということは、もともと、１×２×３×４・・・・という式は何らかの関数の
解析接続であるはずで、
その式を元にしてあのような証明をたてるのはかなり疑問だと思うのですが・・・。
どうでしょうか？？
まあ、題名に「オイラーの」とついていたので、
オイラー時代の考えでともできるの ですが、 どうなんでしょうね？？
| NO.585 | '99 7/19 | 月の光 | 相加平均と相乗平均（１） |
カール君は相加平均≧相乗平均の関係を見て、
次の数列を計算していました。
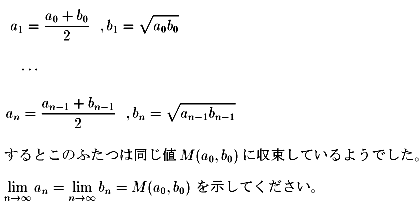
E-mail
戻る