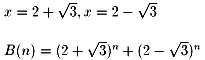
他の2辺はプラス、マイナス1となる。
Weekend Mathematics/コロキウム室/1999.7〜9/NO.66
| NO.564 | '99 7/9 | kiyo | ヘロンの三角形(4) |
ヘロンの三角形の一般式。
三辺を、B−1,B,B+1とする。
漸化式は、
B(n)=4・B(n−1)−B(n)
特性方程式は、X2−4X+1=0
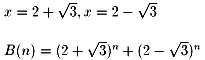
他の2辺はプラス、マイナス1となる。

| NO.565 | '99 7/9 | Junko | ヘロンの三角形(5) |
NO.558
x1=2,y1=1,
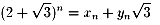 から、
(xn,yn)の一般項を出してみます。
から、
(xn,yn)の一般項を出してみます。
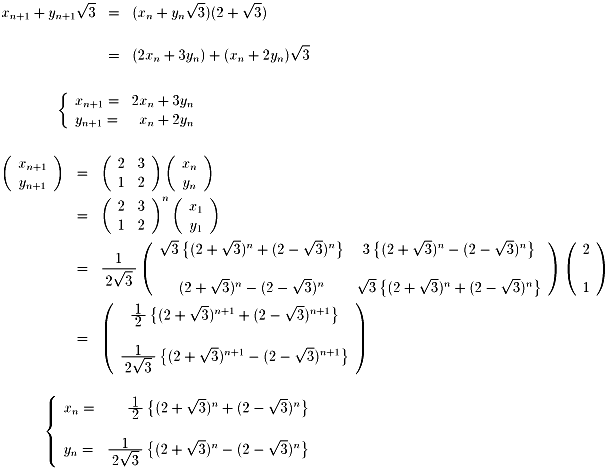
行列のn乗の計算についてここでは省略させてください。
計算間違いをしていないといいのですが・・・。

| NO.566 | '99 7/10 | 数楽者 | ヘロンの三角形(6) |
コロキウムNO.558の1について
これは3の平方根の有理数による近似です。

少なくとも私はそのように理解しています。

| NO.567 | '99 7/10 | ものもの | フェルマ−の大定理 (3) |
フェルマーの問題の拡張
A3+B3+C3=D3
のように3乗で3項なら
33+43+53=63
というものがあります。
4乗で4項なら
A4+B4+C4+D4=E4で
3、4、5、6、7かと思ったが、そうはなりませんでした。
ありそうな、なさそうな?

| NO.568 | '99 7/10 | Junko | フェルマ−の大定理 (4) |
「フェルマ−の最終定理」
| フェルマ−の最終定理 |
| nが3以上の自然数の場合、 「xn+yn=zn」を 満たす整数x、y、zは存在しない。 |
フェルマ−は17世紀のフランス人で、
ツ−ル−ズ地方で法律関係の仕事に従事して生涯を
送った人で、
余暇に数学を研究するのがなによりの楽しみという
変わった趣味(?)の人だったようです。
1637年頃、ギリシャ時代のディオファントスが著した
「算術」という数論の書物を読み、
気づいたことを欄外の余白に書き込んでいった
その中にこの定理があったのです。
さらに、「そのことの真に驚くべき証明を見つけたが、
この余白は狭すぎて書けない」と記されていたのです。
以後、たくさんの数学者がこの証明に挑んだけれども成功しませんでした。
ドイツの数学者クンマ−は19世紀中頃に、
100以下の指数nではフェルマ−の定理が成り立つことを含む
一般的な定理を証明しました。
このクンマ−の開発した代数的整数論という理論を深く究める
ことによって、1994年の初めにはnが400万以下であれば、
フェルマ−の定理が正しいことがわかるところまできていました。
しかし、たとえ400万でも、1兆でも、すべてではないのです。
そして1994年10月、「すべての場合において」フェルマ−の定理が正しいことが
イギリス人アンドリュ−・ワイルズによって証明されたのです。
優秀な若手の数学者が集まって論文を隅から隅までつついてみた結果
「まず間違いはない」と結論し、
最終的には1995年2月、プリンストン大学から出ている雑誌「Annals of Mathematics(数学年報)」
(ワイルズはこれに投稿した。)の編集委員会がワイルズの証明には
間違いがないと結論を下したのです。
かくして、この人騒がせな予想は360年余を経て
最終的に定理となったのです。
(参考:「フェルマ−の大定理が解けた!」足立恒夫著ブル−バックス)

| NO.569 | '99 7/10 | Junko | ト−ナメント戦(1) |
夏の高校野球の地区予選が始まっているようですが、神奈川大会も今日開会式がありました。
横浜スタジアムでの開幕第1戦は、私の前任校である県立大船高校と、県立厚木南高校でした。
大船高校は先取点を取り、試合を有利に展開しながらも、途中逆転されはらはらさせられましたが、
結局9−8で初戦を突破しました。
昨年は80回の記念大会ということで、神奈川を東西2つに分け、
2校が甲子園への切符を手にしました。
東神奈川大会の優勝校、横浜高校が松坂投手の活躍で甲子園でも優勝したことは記憶に新しいところです。
今年は例年通り神奈川県全体での大会となり、出場校も205校と全国1の激戦区となっています。
さて205校で優勝を争う今年の神奈川大会、試合総数はいくつでしょう?

| NO.570 | '99 7/11 | 水の流れ | スターウォーズグッツ(1) |
某飲料水メーカーは50種類のスターウォーズグッツをおまけに入れて、
販売を始めました。
このおまけグッツはすべての種類がランダムに当確率に出回っています。
このグッツを少なくとも1つずつ全種類を集めるまで1回に1本ずつ買うとする。
N本を買った個数とするとき、この平均を求めてください。
また、一般にr種類のグッツを少なくとも1つずつ集めるとき、
平均何本買う必要がありますか。

| NO.571 | '99 7/12 | 水の流れ | 三角数は平方数?(1) |
太郎さんは、高校でパスカルの三角形の美しさを教えています。
そこで、問題です。
問題1:
x2=2y2+1(一つのペル方程式)である、
正の整数解(x、y)を求めてください。
一部の特殊解でも良いですし、一般解でも良いです。
問題2:
子供とき、おはじきで遊んだことがあります。
正方形に並べたおはじきをくずして、
今度は正三角形にも並べることができたとき、
これらのおはじきの個数を求めたくなりました。
1つの例でも良いですし、一般の場合でも良いです。
皆さん、考えてください。
太郎さんも童心にかえって、いろいろとおはじきを並び替えて、
考えていましたが、なかなかうまくいきません。
皆さんも、考えてください。

| NO.572 | '99 7/12 | kiyo | 三角数は平方数?(2) |
(1)
(X,Y)=(3,2),(17,12),(99,70),(577,408)・・・
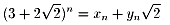
(2)
36,1225,41616,1413721,48024900,・・・
漸化式
C(1)=0,C(2)=1
C(n)=34・C(n−1)−C(n−2)+2
前回と同じアプローチです。

| NO.573 | '99 7/12 | 水の流れ | ト−ナメント戦(2) |
試合数は205チームが戦う場合、
1試合ごとに1チームが敗退していきますから、優勝するまでに、
204チームは敗退しなければないません。
したがって、答えは全部で204試合行うことになります。
ちなみに、1回戦不戦勝の学校は256−205=51チームあります。

| NO.574 | '99 7/12 | Junko | ト−ナメント戦(3) |
今年の高校野球神奈川県大会は205校で争うわけですが、
ト−ナメント方式ですから負ければそれで終わりです。
これで優勝するためには何試合連続で勝てばいいのでしょうか?

 E-mail
E-mail
 戻る
戻る