Weekend Mathematics／コロキウム室／1999.7〜9／NO.65

オイラーの「無限解析入門（１）」第１１夜の始まり、始まり。
今度は、ある自然数ｎを同じものを許す方法で、 自然数の和で表わす方法をＣ（ｎ）とします。 これは、＜水の流れ＞にある第１９回の応募問題のＧの中にでてくる Ｓ（ｍ）と同じ問題です。
そこで、この中にあるＴ（ｍ、ｋ）の表をｍ＝１０まで、 完成しておいてください。素敵な三角形の表になります。
前に、パスカルの三角形、モンモールの三角形と言いましたから、 オイラーの三角形としましょう。　次のようになります。

ｍ	Ｓ（ｍ）	Ｔ（ｍ、ｋ）
		１	２	３	４	５	６	７	８	９	１０
１	１	１
２	２	１	１
３	３	１	１	１
４	５	１	２	１	１
５	７	１	２	２	１	１
６	１１	１	３	３	２	１	１
７	１５	１	３	４	３	２	１	１
８	２２	１	４	５	５	３	２	１	１
９	３０	１	４	７	６	５	３	２	１	１
１０	４２	１	５	８	９	７	５	３	２	１	１

以上です。例の漸化式で増やしていきました。
ところが、オイラーは偉大でした。そこで、今夜の宿題です。
次の母関数を展開してください。

f（ｘ）＝	(１＋ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６＋ｘ７＋ｘ８＋ｘ９＋ｘ１０＋・・・)
	(１＋ｘ２＋ｘ４＋ｘ６＋ｘ８＋ｘ１０＋・・・) (１＋ｘ３＋ｘ６＋ｘ９＋・・・)
	(１＋ｘ４＋ｘ８＋・・・) (１＋ｘ５＋ｘ１０＋・・・) (１＋ｘ６＋・・・)
	(１＋ｘ７＋・・・) (１＋ｘ８＋・・・) (１＋ｘ９＋・・・) (１＋ｘ１０＋・・・)

NO.530で提起された問題 「完全数のすべての約数の逆数の和は２であることを証明してください。」
について考えてみました。

最初の完全数「６」についていえば、その約数の逆数の和は、 1+1/2+1/3+1/6＝2であり確かに和は２になっています。
この式の全体を６倍すると、6+3+2+1＝2・6＝12となり、これはまさに完全数の定義です。

２番目の完全数28について逆に考えれば、完全数の定義から、1+2+4+7+14+28＝2・28
この式の両辺を28でわることで、1/28+2/28+4/28+7/28+14/28+28/28＝2
従って、1/28+1/14+1/7+1/4+1/2+1=2
ということで、約数の逆数の和が２になることがわかります。 約数の順番は入れ替わりますが、同じ面々が今度は逆数で並ぶことになります。

一般には完全数Nの約数を小さい順に、a₁(=1)､a₂､･･･､a_n(=N)とします。
完全数の定義より、a₁+a₂+･･･+a_n=2N
この式の両辺をNで割ることで、
a₁/N+a₂/N+･･･+a_n/N=2
a₁･a_n=N､a₂･a_n-1=N､･･･より、
1/a_n+1/a_n-1+･･･+1/a₁=2
となり、約数の逆数の和が２になるわけです。

特製のサイコロは面の数が偶数の場合に拡張できますね。 ８面体の場合は解が複数あります。

第２１回数学的な応募問題

太郎さんは、高校で三角形の面積を求めるのに、 ヘロンの公式を教えています。 そこで、３辺の長さとその面積がともに整数となる三角形を ヘロンの三角形と言います。 だから、この性質を持つ三角形を知っていたいと、思っていました。 ここで、特に、３辺の長さが連続する３つの自然数の場合を考えます。

問題１：
ｘ^２＝３ｙ^２＋１（一つのペル方程式） である、負でない整数解（ｘ、ｙ）を求めてください。 一部の特殊解でも良いですし、一般解でも良いです。

問題２：
３辺の長さが連続する３つの自然数で、 その面積も整数である三角形の例をいくつか、 考えてください。

太郎さんも童心にかえって、いろいろと数字を順に変えて、 考えていましたが、　なかなかうまくいきません。 皆さんも、考えてください。　

1. （Ｘ_１＝２，Ｙ_１＝１）， （Ｘ_２＝７，Ｙ_２＝４），・・・
   

   一般には次の式で与えられます。

   
   
   

2. 簡単なベーシックのプログラムを組んでいくつか例を出して数列サイトでカンニングしました。

   　
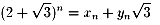
   　　FOR I=1 TO 100000
     　　 FOR J=I+1 TO I+1
         　　FOR K=J+1 TO J+1
          　　  LET  S=(I+J+K)/2
          　　  LET  S1=(S*(S-I)*(S-J)*(S-K))^0.5  ヘロンの公式
          　　  LET  S2=INT(S1)
          　　  LET  S3=S1-S2
          　　  IF S3=0 THEN PRINT I;J;K;S1　条件を満たす３辺と面積
         　　NEXT K
      　　NEXT J
   　　NEXT I
   END
   

   
   
   

   辺 a	辺 b	辺 c	面積
   ３	４	５	６
   １３	１４	１５	８４
   ５１	５２	５３	１１７０
   １９３	１９４	１９５	１６２９６
   ７２３	７２４	７２５	２２６９７４
   ２７０１	２７０２	２７０３	３１６１３４０
   １００８３	１００８４	１００８５	４４０３１７８６
   ３７６３３	３７６３４	３７６３５	６１３２８３６６４

   
   
   　１番短い辺をＨ（ｎ）とする。 漸化式は、
   Ｈ（１）＝３，Ｈ（２）＝１３
   Ｈ（ｎ）＝４×Ｈ（ｎ−１）−Ｈ（ｎ−２）＋２　となっていました。
   Ｈ（３）＝４×１３−３＋２＝５１
   Ｈ（４）＝４×５１−１３＋２＝１９３
   

Weekend Mathematics ではきれいな図や数式をふくむgifファイルが使われていま すが、 どのようなソフトで作成しているのでしょうか。よろしければ教えていただ けないで しょうか。 先月の多角形の問題で私のメールがきれいに書き直してもらっ てあって、感激しました。

数式をかくのには、「PLATeX」というソフトを使っています。 これは数学的記述を多く含んだ書籍の作成を意図して作られた組版システムで、 Donald　E.Knuth　という人が開発しました。 基本的には無償で配布されています。 大きな書店に行くと、関連の書籍が見つかるでしょう。 その中のいくつかには、インスト−ル用のＣＤ−ＲＯＭ がついていると思います。
このソフトを使うと数式を自由自在にかくことができます。 図もかけるのですが、勉強不足の私は、まだそこまでいっていません。

図は、windows付属の「ペイント」で書いています。

グラフなどは「mathematica」を使っています。 これがまたすぐれものです。 数学に関するあらゆることをやってくれます。 詳しくは、wolframのペ−ジ

いずれにせよ、できた画像はgifに変換し、周囲を透過して使っています。 その際には、「Gix Pro」というシェアウエアを使っています。 これは雑誌などの付録ＣＤ−ＲＯＭなどで手に入ります。 タスカホ−ムペ−ジからダウンロ−ドすることもできます。 シェアウエアですから継続して使用する場合は代金(\2310)を支払って、ユ−ザ−登録をしましょう。

「オイラーの無限解析入門（１）」第１２夜の始まり、始まり。
昨夜、オイラーの三角形を作ってみました。 意味のある数字が並んでいますね。 夜空に輝いている星のように、美しき並んでいます。 このＳ（ｍ）の数列を並べてみましょう。
１，２，３，５，７，１１，１５，２２，３０，４２，・・・
何とかして、漸化式みたいのがあれば、計算しやすいのにと、 流れ星の願を賭けていたとき、偶然にも、天使様から、 「理系の数学：５月号」（現代数学社：石谷茂）を読んでみなさいと お告げがありました。 これを参考しして、書きます。
前夜の母関数を展開した係数がＳ（ｍ）ですが、 これでは大変な労力です。 そこで、無限等比等比数列の和の公式を用いて、ｆ（ｘ）を簡単にしましょう。

ｆ（ｘ）＝１÷（１−ｘ）（１−ｘ^２）（１−ｘ^３） （１−ｘ^４）（１−ｘ^５）（１−ｘ^６） （１−ｘ^７）（１−ｘ^８）（１−ｘ^９） （１−ｘ^１０）・・・

この分母を

Ｆ（ｘ）＝（１−ｘ）（１−ｘ^２）（１−ｘ^３） （１−ｘ^４）（１−ｘ^５）（１−ｘ^６） （１−ｘ^７）（１−ｘ^８）（１−ｘ^９） （１−ｘ^１０）・・・

とおいて、　計算してみる方が易しくみえます。
そこで、今夜の宿題です。この計算をしてください。 美しく輝く天の川のように、オイラーの恒等式が見えてきますよ。 お休みなさい。

三角形の三辺の長さをａ，ｂ，ｃとしたときに面積Ｓを与える次の式を、 へロンの公式と呼んでいます。

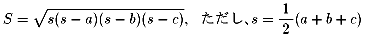
さてここで、三角形の３辺は連続した自然数ということですから、 ｂ−１，ｂ，ｂ＋１とします。

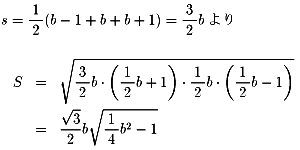
面積Ｓが整数となるためには、ｂは遇数である必要があります。 そこで、ｂ＝２ｋとおきます。（ｋは正の整数）

ｋはもちろん正の整数ですから、これで問題１の方程式ｘ^２＝３ｙ^２＋１に帰着されたわけです。
NO.558で、「kiyo」さんが求めてくださった解を２，３代入してみます。

• ｒ_１＝１，ｋ_１＝２とすると、
  ｂ＝２ｋ＝４、従って３辺の長さは３，４，５、面積は６
  
• ｒ_２＝４，ｋ_２＝７とすると、
  ｂ＝２ｋ＝１４、従って３辺の長さは１３，１４，１５、面積は８４
  
• ｒ_３＝１５，ｋ_３＝２６とすると、
  ｂ＝２ｋ＝５２、従って３辺の長さは５１，５２，５３、面積は１１７０
  

正８面体のサイコロについて、特製サイコロを具体的に作ってみようと思います。

NO.551でやったのと同じように、
ｘ＋ｘ^２＋ｘ^３＋ｘ^４ ＋ｘ^５＋ｘ^６＋ｘ^７＋ｘ^８ の因数分解を考えます。

ｘ＋ｘ^２＋ｘ^３＋ｘ^４ ＋ｘ^５＋ｘ^６＋ｘ^７＋ｘ^８ ＝ｘ（１＋ｘ）（１＋ｘ^２）（１＋ｘ^４）
と因数分解できますので、ｘ・（項数２）・（項数４）という変形が３通り考えられます。

ｘ＋ｘ２＋ｘ３＋ｘ４ ＋ｘ５＋ｘ６＋ｘ７＋ｘ８	＝ｘ（１＋ｘ＋ｘ２＋ｘ３）（１＋ｘ４）・・・（１）
	＝ｘ（１＋ｘ２＋ｘ４＋ｘ６）（１＋ｘ）・・・（２）
	＝ｘ（１＋ｘ＋ｘ４＋ｘ５）（１＋ｘ２）・・・（３）

これを組み替えて、（項数８）・（項数８）という形を_３Ｃ_２＝３通り作れると思います。
（１）、（２）の組み合わせで特製サイコロを作ってみます。

＝（ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６＋ｘ７＋ｘ８）・ （ｘ＋ｘ２＋ｘ３＋ｘ４＋ｘ５＋ｘ６＋ｘ７＋ｘ８）

＝ｘ（１＋ｘ＋ｘ２＋ｘ３）（１＋ｘ４）・ ｘ（１＋ｘ２＋ｘ４＋ｘ６）（１＋ｘ）

＝ｘ（１＋ｘ＋ｘ２＋ｘ３）（１＋ｘ）・ ｘ（１＋ｘ２＋ｘ４＋ｘ６）（１＋ｘ４）

＝（ｘ＋２ｘ２＋２ｘ３＋２ｘ４＋ｘ５）・ （ｘ＋ｘ３＋２ｘ５＋２ｘ７＋ｘ９＋ｘ１１）

＝（ｘ＋ｘ２＋ｘ２＋ｘ３＋ｘ３＋ｘ４＋ｘ４＋ｘ５）・ （ｘ＋ｘ３＋ｘ５＋ｘ５＋ｘ７＋ｘ７＋ｘ９＋ｘ１１）

というわけで２つのさいころを、「１，２，２，３，３，４，４，５」と「１，３，５，５，７，７，９，１１」とすればいいということがわかります。
和を表にしたものを下に示します。 右に、普通の正８面体サイコロの表を並べておきます。

１ ３ ５ ５ ７ ７ ９ １１ １ ２ ４ ６ ６ ８ ８ １０ １２ ２ ３ ５ ７ ７ ９ ９ １１ １３ ２ ３ ５ ７ ７ ９ ９ １１ １３ ３ ４ ６ ８ ８ １０ １０ １２ １４ ３ ４ ６ ８ ８ １０ １０ １２ １４ ４ ５ ７ ９ ９ １１ １１ １３ １５ ４ ５ ７ ９ ９ １１ １１ １３ １５ ５ ６ ８ １０ １０ １２ １２ １４ １６

１ ２ ３ ４ ５ ６ ７ ８ １ ２ ３ ４ ５ ６ ７ ８ ９ ２ ３ ４ ５ ６ ７ ８ ９ １０ ３ ４ ５ ６ ７ ８ ９ １０ １１ ４ ５ ６ ７ ８ ９ １０ １１ １２ ５ ６ ７ ８ ９ １０ １１ １２ １３ ６ ７ ８ ９ １０ １１ １２ １３ １４ ７ ８ ９ １０ １１ １２ １３ １４ １５ ８ ９ １０ １１ １２ １３ １４ １５ １６

E-mail 戻る