Weekend Mathematics/コロキウム室/1999.4〜6/NO.58
| NO.493 | '99 5/25 | 水の流れ | ダーツの期待値(1) |

太郎さんは、先日のゴールデンウイークに、 岐阜県大垣市長松にある電気店パナシーズンの大売り出しに行って来ました。 ここで、問題です。
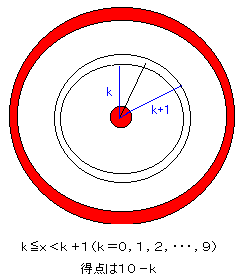
この電気店では、図1のような丸い的でダーツ競技を行っていました。
中心がOで、半径10の円板が的でして、
同心円上に、半径9,8,7,…、2,1の円が書いてありました。
得点は小さい円環(一番小さいのは円)から順に、
10点、9点、8点、…、最後は1点でした。この得点分だけ、
参加者に賞品がもらえます。
円板内の点をまったくでたらめに1回選んだときの得点の
期待値を求めてください。
太郎さんは童心にかえって、ダーツ競技を楽しんでいましたが、
この電気店にとって、賞品の数をどれだけ用意しておいたか、
気になってしかたがありません。
皆さんも、考えてください。

| NO.494 | '99 5/25 | 水の流れ | 置換積分(7) |
NO.490にあるハイポサイクロイドで囲まれた図形の 面積を求めてみました。


| NO.495 | '99 5/25 | Junko | 置換積分(8) |
NO.491にある、モンテカルロ法について
コメントします。
ある図形Aの面積を求めるのに、それを含む正方形Bを考えます。
この正方形の中から任意の点P(x,y)を抽出して、その点P(x,y)が
図形Aの中にあるかどうかを判断します。
これを1,000回繰り返してAの中にあった回数がたとえば521回とすると、
(Aの面積)/(Bの面積)≒521/1,000と考えられるわけです。
こうしてAの面積の近似値を求められるわけですが、
試行回数を10,000、100,000とふやす(コンピュ−タ−があればこそ・・・)ことで、
ある程度の精度を得ることができるわけです。
浜田 明巳のNO.448などは
その例だと思います。
このモンテカルロ法というのは「大数の法則」の基づいています。
「大数の法則」というのは、試行回数Nを十分大きくすると、事象Aの起こる相対度数
r/NはほぼP(A)に等しい、というものです。
それにしてもなぜ、「モンテカルロ」なのでしょう?

| NO.496 | '99 5/26 | Junko | オイラーの「無限解析入門(1)」(12) |

| NO.497 | '99 5/26 | Junko | ダーツの期待値(2) |
円の面積は半径の2乗に比例することに注意して、
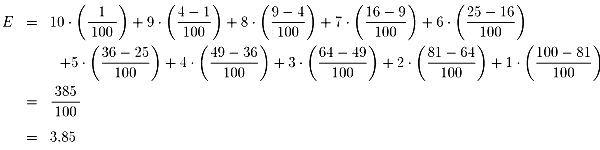

| NO.498 | '99 5/26 | Junko | ダーツの確率(4) |
この問題についてず−っと考えていました。
確率は1/2だそうなあ、と見当をつけていましたが、
はっきりとした根拠を示せずにいました。
また、NO.465で1〜3までの
ヒントに対する解答は得られたのですが、それがどうして4につながっていくのか
わかりませんでした。
幸いにして、このコロキウム室で極座標系による積分を話題にしていくうちに、
だんだんと道が開けてきました。
今日またこの問題を考えていて、「わかった!」と叫んでしまいました。
もやもやしていた霧が一気に晴れたような感じです。
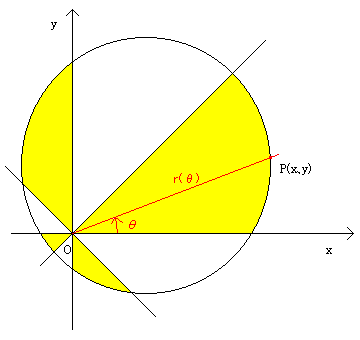
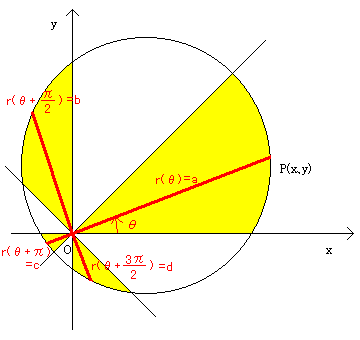
4本の弦が1点で交わっているところを原点に、左上の図のようにダ−ツの的をおきます。
円周上の点P(x,y)と原点を結ぶ線分OPとx軸とのなす角をθとします。
0P=r(θ)とし、極座標系による積分を考えます。
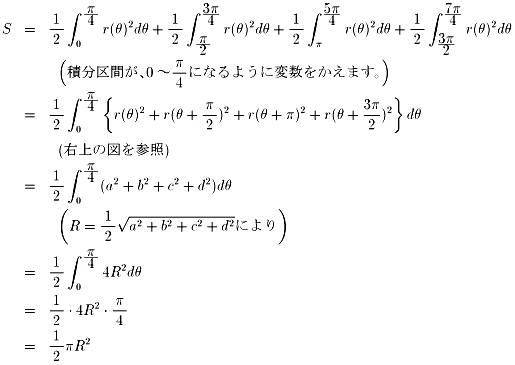

| NO.499 | '99 5/26 | 水の流れ | 置換積分(9) |
モンテ・カルロ法について、大阪書籍発行の「新数学辞典」から引用します。
十分滑らかな境界Γで囲まれた領域Ωにおいて、
Γ上に境界値を与えてΔu=0を解くディリクレ問題の解uの定点x∈Ω
における値u(x)は、xから出発してランダムに動く点
(以下これを「よっぱらい」と呼ぶ)
が境界yにおいてつかまる確率密度をpx(y)とすると、
積分∫ψ(y)dpx(y) で与えられる。
これは本質的に1920年代にウィーナー
(父から天才教育を受け、18歳でハーバード大学卒業、ブラウン運動で有名)
によって研究された結果であり、不正則点やウィーナーの条件など、
この立場から明快に説明される。
1950年代以降確率論的ポテンシャル論のもっとも簡単な一例として
知られるようになった。
いわばよっぱらいがyでつかまるとψ(y)の罰金をとられるとき、
xから出発したよっぱらいがとられる罰金の期待値がu(x)ということである。
これをランダムに動く点をシュミュレートしょうというのが
モンテ・カルロ法による境界値問題の解法である。
提案された当時(1940年末)には奇抜な解法と評判であったが、
詳しい値を求めるにはきわめて多数回の反復を要した。
そこで、私の見解ですが、当時、イタリヤのモナコの近くにあった
モンテカルロという町を巡って行われる自動車のラリーがこのような、
ランダム運動をしたことから、このいわれを取るようになったと考えられる。
全くの推測ですが?

| NO.500 | '99 5/27 | プ−太 | 「理系への数学」 |
最近、雑誌「理系への数学」(旧、BASIC数学)のバックナンバーを
読みました。
そこには、山下純一氏のコラム、入試問題からの旅立ちという僕に
ピッタシ内容がありました。
それに関して、所感を述べさしてください。
そこでは、弘前大の入試問題から発展させて、
次のルベーグの定理を証明していました。
ルベーグの定理: 実数αが0<θ<1で、2進法展開が
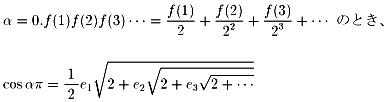
となる。
ここで、e1=1-2f(1), e1e2=1-2f(2),
e1e2e3=1-2f(3),……とする。
僕が、心踊ったのはこれが「無限連無理数」というべきものを
用いて表わされているという点です。
僕は、以前、小数展開や連分数展開があるのなら、「連無理数展開」
といったものがあったっていいじゃないか、と考えた事があったからです。
僕がそれを考えたのは、次の象徴的な事実にまとめられます。
周期小数=有理数=整数係数1次方程式の解→
→周期連分数=2次の無理数=整数係数2次方程式の解→
→「周期連無理数」=
半径1の円周に内接する正多角形のある対角線の長さ(2cos(a/b)π)
=整数係数2のベキ次方程式の解→
このように、1次方程式の解を表わす為に分数が作られ、
それを応用して連分数が作られ、
周期連分数を考えると2次方程式を解く必要が有り、
2次方程式の解を表わす為に平方根が作られ、
それを応用して「連無理数」が作られ、
「周期連無理数」を考えると2のベキ次方程式を解く必要が有り、………。
なんともきれいな、思考の過程だとおもいませんか?
僕の妄想としては、(特殊な)2のベキ次方程式の解を表わす為に
三角関数があるのなら、次に「連三角関数」を考えてもいいんじゃないか、
と考えています。

 E-mail
E-mail
 戻る
戻る