
Weekend Mathematics/コロキウム室/1999.4~6/NO.55
NO.464 '99 5/7 水の流れ オイラーなら?(3)
(5/10一部訂正)
オイラーの公式eix=cos x+isin x(iは虚数単位)を用いると、
三角関数が指数関数に表現できます。
だから、三角関数の微積分は指数関数の微積分になるので、
ex・sin xやex・cos xの形の微分、積分は
オイラーの公式を用いると便利です。
そこで、基本的な考え方を紹介します。
連立方程式
eix=cos x+isin x…①
e-ix=cos x-isin x…②
をsinx、 cos xについて、解くと、
sin x=(eix-e-ix)/2i ,
cos x=(eix+e-ix)/2となります。
このとき、虚数単位iを含む微積分では、
iを通常の定数と同様に扱います。
「月の光」さんは、この考えで、
途中分母を複素数の極形式で表されましたが、
別な方法として、分母の実数化をしてもできます。
(1) ここで、書いてみます。まず、積分からいきます。

(2) 次に、微分です。
f(x) =ex・cos x 、g(x)=ex ・sin x より、
| h(x)= | ex (cos x+isin x) とおくと、 |
| =ex・eix | |
| =e(1+i)x とかける。 |
| h’(x)= | (1+i)・e(1+i)x |
| =(1+i)・ex・eix | |
| =(1+i)・ex(cos x+isin x) | |
| =ex(cos x-sin x)+iex(cos x+sin x) |
皆さん、こんな微積分があったら、
オイラーの公式を使って解いてください。
高校の先生が答案をみて、どんなコメントを言われるか楽しみですね。

NO.465 '99 5/8 Junko ダ-ツの確率(2)
(一部訂正5/10)
NO.462の 「ダ-ツの確率」についてとりあえず3番まで。


NO.466 '99 5/9 水の流れ 最速降下問題(1)
皆さん、NO.415のゼーター関数ζ(2)物語の第13夜<特別寄稿>を思い出してください。
もう一度、ヨハンの考え出した特別問題を書きます。
「異なる高さにある2点を考えます。
この2点をA,Bとし、1点がもう1点の真上にないものとします。
これらの2点を結ぶ直線から円弧、波形に曲がりくねったものまで、
もちろん無数にあるわけです。
そこで、この曲線にそってAからBへボールを転がし落とすと想像して
みて下さい。ボールが上の点から下の点にたどり着くまでにかかる時間は
当然、曲線の形に関わってくることになります。
ベルヌーイはボールが最も短い時間で転がり落ちる
特定の曲線ABを求めよという問題を出して、数学界に挑戦したのです。
彼はこの曲線をギリシャ語の“最短”と“時間”という語からとって
最速降下問題と呼びました。」
ここで、再度、問題を誤解されることがないように、繰り返します。
「与えられた二つの点を結ぶ曲線は無数にありますが、
たとえばその曲線を細い管か溝と考えて、
小さな球をその中に置いて手を放し、
この球が1点からもう1つの点までもっとも短時間に通過する、
そんな曲線を1つあげなさい。」
ヨハンの視界の中にはもっと別な標的がありました。
ヨハンはこう書いています。
「幾何の秘密を見抜いただけでなく、
その分野を拡張したという驚くべき法則を誇っている者たちを含め、
この風変わり問題を解いたという者は現れていない。
ただし、彼らは誰にも知られていないと思っていたらしいが、
その黄金の定理とやらはかなり以前に他の人物によって
発表されていたのである。」
”黄金の定理”とはアイザック・ニュ-トンの発見した流率法をさしています。
ヨハンはこの問題の写しを1697年に、
イギリスの造幣局に務めていたニュートンに発送しました。
当時ニュ-トンは姪のキャサリン・コンドウィットと共に
ロンドンに住んでおり、彼女がこのエピソードに触れています。
「1697年、その問題がベルヌーイから送られてきたとき、
ニュ-トン卿は貨幣大改鋳で大忙しの最中にあり、
ロンドン塔からはやっと4時に戻ってきた。
たいそう疲れていたが、それを解いてしまうまで(朝の4時だった)、
眠ろうとはしなかった。
アイザック・ニュ-トンは当時もうかなりの年齢になっており、
しかも緊張を強いられる日中の仕事でくたびれていたのに、
ヨーロッパの大多数の者が解決できなかった問題に勝利を収めたのです。
それは偉大なる英国の天才の恐るべき威力を
思い知らせる素晴らしい機会になりました。
この続きは、次回にお送りします。
尚、歴史的事実は、参考文献の「数学の知性」(現代数学社)から、
多くの引用をさせて頂いています。

NO.467 '99 5/10 水の流れ 最速降下問題(2)
ニュートン(イギリス:1642~1727)はベルヌーイ兄弟
(スイス兄ヤコブ:1654~1705、弟ヨハン:1667~1748)や
ライプニッツ(ドイツ:1646~1726)が彼の評判や栄光を
打ち砕いてやろうと狙っていることや、
どうせ彼らは自分たちの解を発表してやろうとずうずしながら待ちかまえているに
違いないことをはっきりと感じとっていました。
ですから、ニュートンはこの機会をとらえて、時間が勝負のこの問題をさっさと
解いてしまったのです。多少怒りを込めて彼はこう述べたと言います。
”私は数学上のことで外国人にいじめられるのは好きじゃない”
さてヨーロッパへ戻って、1697年のイースター
(キリストの復活を祝う祭り:春分後の最初の満月の次の日曜日)が近づくにつれ、
いくつかの解がヨハンの下に寄せられました。
誰もが探していた・・・(幾何学者ならよく知っている)
・・・曲線は、外でもない上から下へ向かうサイクロイドでした。
この重要な曲線はパスカル(スランス:1623~1662)と
ホイヘンス(オランダ:1625~1695)によって研究されていましたが、
これが最速降下線にもなることに二人の数学者のどちらも気づいていませんでした。
ヨハンは独特の誇張した言い回しで、
”もし私がこのホイヘンスのサイクロイドこそ求めていた曲線であると言ったら、
あなたがたは驚きのあまり生気を失うであろう”と言っています。
期限であるイースターの日がきました。
ヨハンは合わせて 5つの解を受け取りました。
彼自身のものと、ライプニッツのもの、3つ目が兄ヤコブのもの
(さぞヨハンは落胆したでしょう。解けないと思っていたから)、
ホスピターリ侯爵のものもこれに加わっています。そして、最後が英国の消印のついたものでした。
開封してみると、匿名になっていましたがヨハンはそこに正解を見つけだしました。
彼はアイザック・ニュートンの手強さを思い知らされたのです。
サインこそありませんでしたが、解そのものが迷うことなく天才のサインを示していました。
真実かどうかは怪しいのですが、うれしくなるような伝説が伝えられています。
”私はその爪を見てライオンを識別した”
これで、最速降下線(サイクロイド)にまつわるお話を終わります。
そこで、現代にもどってみます。
東京と大阪を結び最速の乗り物(リニアモターカー)の研究が進んでいますが、
この最速降下線を知っているなら、
是非東京と大阪を結ぶサイクロイドの地下道をつくってもらいたいなー・・・。
また、私自身、興味をもっているのに自然界で、
このサイクロイドの性質を使っている乗り物を見つけたいです。
例えば、ジェットコウスターとか、奈良の東大寺の屋根の優雅な曲線は
雨が自然に早く落ちるように設計されていて、このサイクロイド曲線がモデルかなー・・・。
もし、ご存じ方があれば、お知らせください。
尚、遅くなりましたが、いつものように、
歴史的事実は、参考文献の「数学の知性」(現代数学社)から、多くの引用をさせて頂いています。

| NO.468 | '99 5/10 | Junko | 最速降下問題(3) |
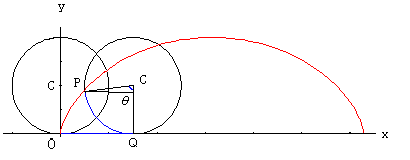
最速降下問題の答えでもある、サイクロイド曲線についてかきます。
右の図のように、直線上を円が転がるときに、
円周上の定点Pが動く軌跡をサイクロイドと呼びます。
この円の半径をa、∠PCQをθとすると、
点P(x,y)は次の様に表示されます。
線分OQ=弧PQであることに注意して、
x=a(θ-sinθ)
y=a(1-cosθ)

| NO.469 | '99 5/10 | 水の流れ | オイラーの「無限解析入門(1)」(7) |
オイラーの「無限解析入門(1)」の第4夜の始まり、始まり。
先日、「月の光」さんによって、第3夜の宿題が見事に、
微分を利用して、一気に解決されました。(NO.461)
「月の光」さん!すごい。
次の等式を書きましたね。

そして、x=ー1を代入すれば、
ψ(-2)、ψ(-3)を求められて、
ζ(-2),ζ(-3) を計算できます。
皆さん、チャレンジしてくださいね。
今夜はこれで終わります。また、次夜をお楽しみに待っててください。

| NO.470 | '99 5/12 | 月の光 | xn+yn=zn(4) |
問題
フェルマーの定理を n=3,4,5… のときなど、
できる範囲で証明してください。
ただし、x,y,z は自然数とします。
n=4 のときに挑戦してみました。
x4+y4=z4 を満たす自然数 x,y,z は存在しない。
証明) x,y,z は自然数なので x<z,y<z …(1)
x4=z4-y4=(z2+y2)(z+y)(z-y)
(1)より x2<z2<z2+y2
だから x3=z2+y2 …(2)
または x4=z2+y2 …(3)
(2)のとき、(1)より x<z<z+y なので x=z-y , z+y=1
これは zとyが自然数なので有り得ない。
(3)のとき、z2-y2=1 , z2=y2+1
しかし、y2<y2+1<y2+2y+1 から
y<
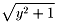 <y+1
<y+1
yは自然数なので z2=y2+1 を満たす自然数 z は存在しない。
よって x4+y4=z4 を満たす自然数
x,y,z は存在しない。

| NO.471 | '99 5/13 | Junko | オイラーの「無限解析入門(1)」(8) |
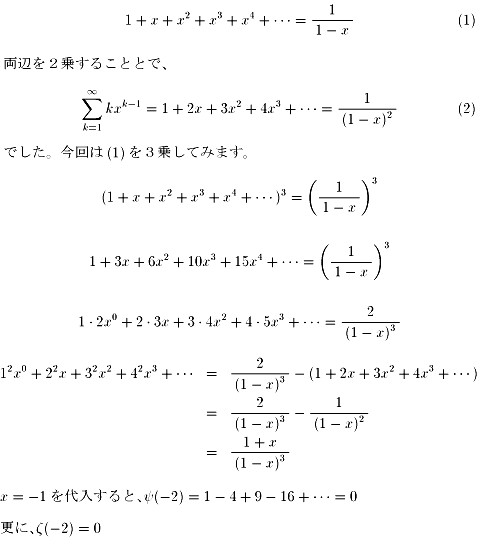
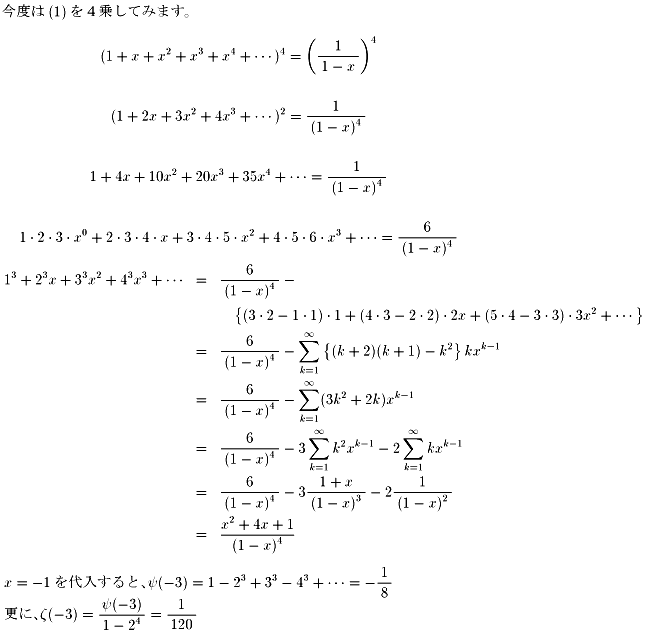

| NO.472 | '99 5/14 | プ-太 | xn+yn=zn(5) |
NO.470の
x4+y4=z4 を満たす自然数 x,y,z は存在しない
という証明の以下の部分について、大変恐縮ながら
間違った証明をされているものと思われます。
x,y,z は自然数なので x<z,y<z …(1)式の因数分解は、そのまま数の素因数分解になってはいません。 z2+y2は、例えば(x3.5)とか (x4)/3かもしれません。 ただし、もちろん (x3.5)とか(x4)/3が整数であった場合ですが。
x4=z4-y4=(z2+y2)(z+y)(z-y)
(1)より x2<z2<z2+y2 だから x3=z2+y2 …(2)
または x4=z2+y2 …(3)
フェルマーの大定理のn=3,4のときの証明が、
初等整数論講義(高木貞治)にのってあります。
大学2,3年生のレベルだと思われます。
もし、証明をこのコロキウムに
載せるためには、準備と証明自身で、
(本に換算して)10ページ前後必要だと思われます。
ちなみに、初等整数論講義(高木貞治)では二次体をつかって
証明してあります。

| NO.473 | '99 5/15 | Junko | ビュッフォンの針の実験(3) |
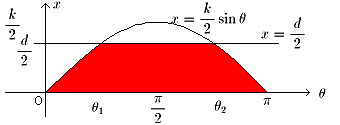
d<kの場合について考えました。
右の図の赤い部分の面積を求めればいいことになります。
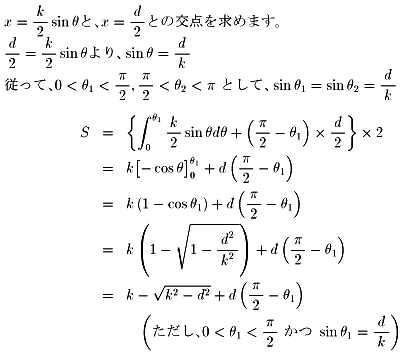

 E-mail
E-mail
 戻る
戻る