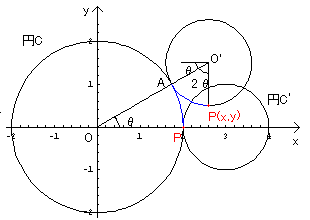
Weekend Mathematics/コロキウム室/1999.4~6/NO.57
| NO.483 | '99 5/21 | Junko | 置換積分(2) |
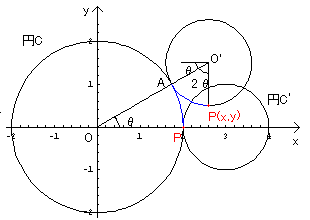
右の図のように、円Cと円C’との接点をAとする。
APの長さが等しいことと、円Cの半径が、円C’の半径の2倍であることを
考慮すると、
x軸とOAとのなす角θに対して、∠AO’Pは2θとなる。
従って、P(x,y)とすると、
x=3cosθ+cos(π+3θ)=3cosθ-cos3θ,
y=3sinθ+sin(π+3θ)=3sinθ-sin3θ
(0≦θ<2π)となります。
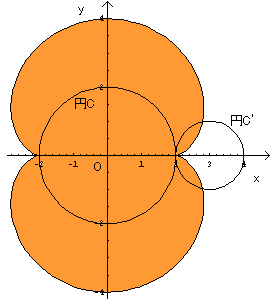
点Pの軌跡は右の図のようになります。
円Cと円C’も一緒にかいてあります。
問題はオレンジの部分の面積を求めることになります。

| NO.484 | '99 5/21 | Junko | 最大値なし |
青山学院大学経営学部の数学の入試問題に出題ミスがあったとか・・・。
|
x,yが、2x+3y=1,-1≦x≦1を満足しているならば、
8x-5×9y-2x+1+1は、 x=□のとき、最大値□をとる。 |
2x=X、3y=Yとおくと、X+Y=1
z=8x-5×9y-2x+1+1とする。
| z | =X3-5Y2-2X+1 |
| =X3-5(1-X)2-2X+1 | |
| =X3-5X2+8X-4 |
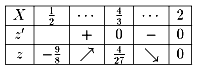
従って、zの最大値は4/27で、このときのX=4/3(x=2-log23)
という解答を想定したのでしょうか?
これには間違いがあります。
3y=Yとおいていますから、Y>0です。従って、Y=1-X>0よりX<1、
つまりXのとりうる範囲は、1/2≦X≦2ではなく、1/2≦X<1です。
この範囲で新たに増減表を書いてみると、
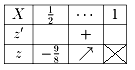
従って「最大値はない」ということになります。
2x+3y=1とした時点で、-1≦x≦1はあり得ないということです。
実際には-1≦x<0です。
また最初の解答で、zは、xとy(置き換えにより、XとYの)の2変数関数ですから、
最大となるときのX(x)だけでなく、Y(y)も確認していれば、
おかしいということに気づいたのにと思います。

| NO.485 | '99 5/21 | Junko | オイラーの「無限解析入門(1)」(10) |
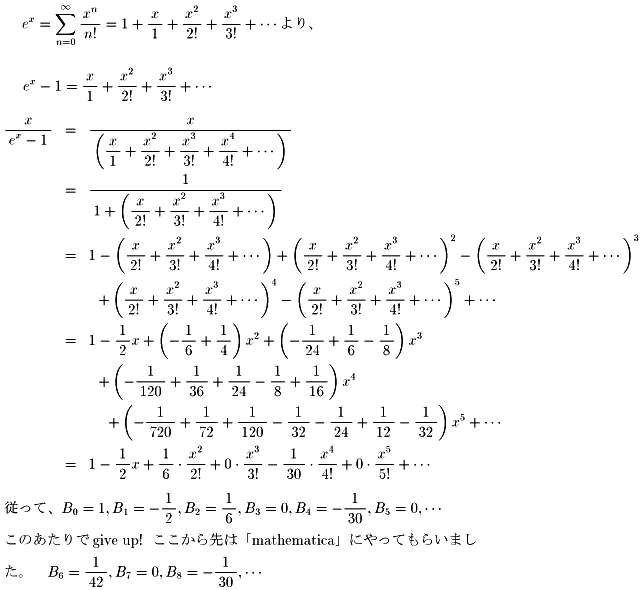

| NO.486 | '99 5/21 | 水の流れ | 置換積分(3) |
NO.482の後の解答は、
極方定式 r=f(θ)の面積を求める公式に
入れて計算してありますが、
点Pとx軸とのなす角はθではありません。
だから、ここで間違っています。
ちなみに円C’は何回転しますかは、もうお分かりでしょう。
3回転します。
この軌跡をエピ・サイクロイド(外サイクロイド)といいます。
円C’を内側で、円Cに接しながら滑ることなく回転させると、
こちらは1回転しかしません。そして、この場合は円Cの内部で
y軸上を動くことになるでしょう。
また、軌跡の名称は忘れましたが、(内サイクロイドと言います)

| NO.487 | '99 5/22 | Junko | ダ-ツの確率(3) |

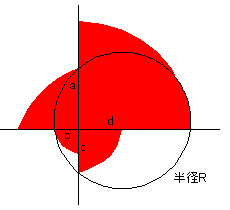
円の4分割は任意ですから、これもまたおもしろい結果だなあと思うのです。

| NO.488 | '99 5/22 | Junko | 置換積分(4) |
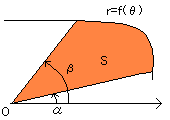
極座標系における面積の求め方です。
原点からの距離rが、偏角θの関数として、r=f(θ)として表されているとき、
左図の面積Sは以下の定積分によってもとめるこができます。
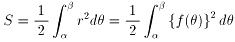
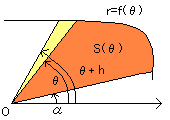
どうして上の式で面積を求めることができるのか、 感覚的にではありますがこじつけてみます。


| NO.489 | '99 5/23 | 水の流れ | オイラーの「無限解析入門(1)」(11) |
オイラーの「無限解析入門(1)」の第6夜の始まり、始まり。
Junkoさんが見事にBernoulli数がTaylor展開によって、求められました。
数式ソフト「Mathematica」と共にJunkoさんの能力も素晴らしい。
解析概論を読んでいたら、Bernoulli数を別の角度から、
求めてありましたので、紹介します。
-2π<x<2π において、
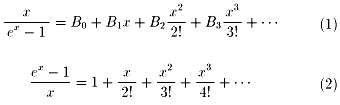
この2式を掛けると、明らかに右辺は1になります。
そして、当然 B0=1 であり、xnの係数は 0 です。
これを左辺で見ますと、
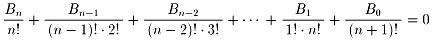
両辺に(n+1)! を掛けて 、2項係数で表すと
n+1C1Bn+
n+1C2Bn-1+
n+1C3Bn-2+
・・・+
n+1CnB1+
n+1Cn+1B0=0
これは n+1 のところを n で書き直し、さらに組合せの性質もつかって、
nCn-1Bn-1+
nCn-2Bn-2+
・・・+
nC2B2+
nC1B1+
nC0B0=0
これは(B+1)n-Bn=0 と書けば分かり易いです。
ただし、展開後の B の指数を下の添え字にしてください。
ここで、n=2 を代入して 2B1+1=0 ∴B1=-1/2
n=3 を代入して 3B2+3B1+1=0 ∴B2=1/6
n=4 を代入して 4B3+6B2+4B1+1=0 ∴B3=0
n=5 を代入して 5B4+10B3+10B2+5B1+1=0 ∴B4=-1/30
後は、読者に任せます。分かったことは
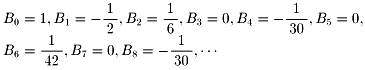
(B1以外の奇数番号のBnは0になっています)
ここで、ゼーターの値 ζ(0)=-1/2,ζ(-1)=-1/12,ζ(-2)=0, ζ(-3)=1/120,・・・を比較してください。 すると、
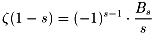
と簡単に書けることをオイラーは1749年に発見しました。
さて、ζ(2),ζ(3),ζ(4),・・・とB2、B3,B4,
・・・の関係については、オイラーは
すでに1735年に見つけていました。
ここの関係を発見するにはガンマ関数Γ(s)の登場になります。
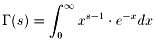
と書きます。
ここで、やっと、今夜の宿題です。
このガンマ関数Γ(s)の下記の性質を示してください。
(1) Γ(s+1)=sΓ(s) 、Γ(1)=1
(2) Γ(s+1)=s!
この先の展開に不安を持ちつつ、第6夜はゆっくりねましょう

| NO.490 | '99 5/24 | Junko | 置換積分(5) |
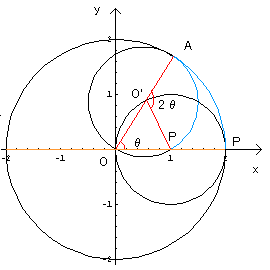
円C’を内側で、円Cに接しながら滑ることなく回転させたときの
軌跡は、「ハイポサイクロイド」というそうです。
点Pはy軸上を(2,0)から(-2,0)まで行き、また戻ってきます。
(オレンジの部分)
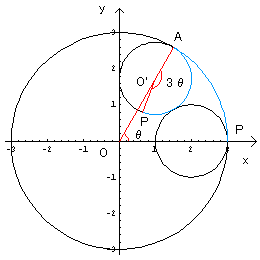
半径の比を1:2とすると、線分になってしまっておもしろくないので、
今度は半径の比を1:3にしてみます。
円Cと円C’との接点をAとします。
APの長さが等しいことと、円Cの半径が、円C’の半径の3倍であることを
考慮すると、x軸とOAとのなす角θに対して、∠AO’Pは3θとなる。
従って、P(x,y)とすると、
x=2cosθ+cos(-2θ)=2cosθ+cos2θ,
y=2sinθ+sin(-2θ)=2sinθ-sin2θ
(0≦θ<2π)となります。
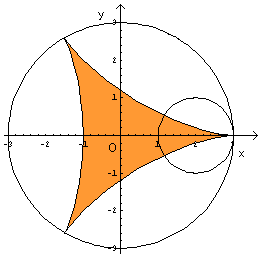
これを図示するとこうなります。
この曲線で囲まれた部分の面積も求めてみてください。

| NO.491 | '99 5/24 | 浜田 明巳 | 置換積分(6) |
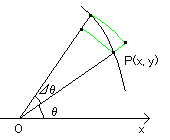

これをいつものようにBASICのプログラムで検証しました.昔の話なので,N88日本語BASICで作ってあります.
100 'SAVE"97OOSAK3.BAS",A 110 *INIT:SCREEN 3,0,1:CLS 3:SCREEN ,,0,1:CLS 3:CONSOLE 0,25,0,1:WIDTH 80,25 120 ON STOP GOSUB *STP:STOP ON:ON ERROR GOTO *ER 130 DIM X(180),Y(180):LOCATE 44,12:PRINT"97年大阪府立大" 140 R=2:RR=1 '大円,小円の半径 150 X0=0:Y0=0:X1=X0+R+RR:Y1=Y0:S1=0:S2=0:S3=0:S4=0:S5=0 160 T=0:X(0)=X1-RR:Y(0)=Y1:KK=49:XC=320+2*KK:YC=200:ACT=0:PI=3.14159:W=PI/180 170 ' 180 *ST:GOSUB *SAKUZU 190 LOCATE 0,0:PRINT"何かキーを押して下さい.始めます." 200 WHILE INKEY$="":WEND:WHILE INKEY$<>"":WEND:LOCATE 0,0:PRINT SPC(34) 210 FOR T=0 TO 180:TT=2*T 220 X1=X0+(R+RR)*COS(TT*W):Y1=Y0+(R+RR)*SIN(TT*W) 230 X(T)=X1-RR*COS((RR+R)*TT*W):Y(T)=Y1-RR*SIN((RR+R)*TT*W) 240 ON -(T=0) GOTO 320 250 S1=S1+.5*ABS((Y(T)-Y(T-1))*(X(T)+X(T-1))) 260 S2=S2+.5*ABS(X(T-1)*Y(T)-X(T)*Y(T-1)) 270 A=SQR(X(T)*X(T)+Y(T)*Y(T)):B=SQR(X(T-1)*X(T-1)+Y(T-1)*Y(T-1)) 280 C=SQR((X(T)-X(T-1))*(X(T)-X(T-1))+(Y(T)-Y(T-1))*(Y(T)-Y(T-1))) 290 S=.5*(A+B+C):S3=S3+SQR(S*(S-A)*(S-B)*(S-C)) 300 S4=S4+.5*A*B*SIN(2*W) 310 S5=S5+.25*(A*A+B*B)*2*W 320 ACT=1-ACT:DISP=ACT*16+1:SCREEN ,,ACT:CLS 2 330 GOSUB *SAKUZU:LOCATE 0,4:PRINT"t=";TT;"°":PRINT 340 COLOR 2:PRINT"面積=4∫(0,4)xdy":PRINT USING" =##.####*π";S1/PI:PRINT 350 PRINT"面積=∑.5*abs(x1*y2-x2*y1)":PRINT USING" =##.####*π";S2/PI:PRINT 360 PRINT"面積=∑(ヘロンの公式)":PRINT USING" =##.####*π";S3/PI:PRINT 370 PRINT"面積=∑.5*OP1*OP2*sin(⊿t)":PRINT USING" =##.####*π";S4/PI:PRINT 380 PRINT"面積=∑.5*OP^2*⊿t":PRINT USING" =##.####*π";S5/PI:COLOR 7 390 SCREEN ,,,DISP 400 ON -(INKEY$="S") GOSUB *SS 410 NEXT:WHILE INKEY$<>"":WEND 420 LOCATE 0,0:PRINT"繰り返しますか?(Y/N)":A$="" 430 WHILE A$<>"Y" AND A$<>"y" AND A$<>"N" AND A$<>"n" 440 A$=INKEY$:WHILE INKEY$<>"":WEND 450 WEND 460 IF A$="Y" OR A$="y" THEN RUN 470 LOCATE 0,0:PRINT"終わりました. " 480 ' 490 *STP:END 500 ' 510 *ER:RESUME NEXT 520 ' 530 *SAKUZU:CIRCLE(XC+KK*X0,YC-KK*Y0),KK*R,7 540 CIRCLE(XC+KK*X1,YC-KK*Y1),KK*RR,6 550 FOR J=0 TO T:CIRCLE(XC+KK*X(J),YC-KK*Y(J)),2-(J=T),2-3*(J=T),,,,F:NEXT 560 RETURN 570 ' 580 *SS:WHILE INKEY$="":WEND:WHILE INKEY$<>"":WEND:RETURNこのプログラムによると,
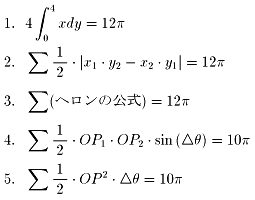
となります.
1.は通常の積分計算,2~4は原点を1つの頂点とし,
その頂点の角を2度(=π/90)とする微小の三角形に分割して
面積の和を求めた計算,5は原点を中心,
中心角2度の微小の扇形に分割して面積の和を求めた計算です.
これでどうやら⊿θ(=2度)がからんだ計算だと10πになり,
そうでないと12πになることが分かりました.
しかしどれも同じ部分の面積を求める式のはずです.
ここら辺で頭がこんがらがってしまったのです.
どうか皆さん,助けて下さい.
他にモンテカルロ法でもプログラムを作ってみたのですが,
面積は12πになりました.
正解は絶対に12πという事は分かっているのですが・・・.

| NO.492 | '99 5/24 | 水の流れ | フェルマ-の大定理 |
フェルマ-の大定理は本当に解決したでしょうか。
先日、下記のようなメールが届きましたので、お知らせします。
誰か、この信憑性について、ご存じの方教えてください。
<水の流れ>さんは
ホームページ
の中で、
「フェルマーの大定理は
1994年10月7日に発表した論文には四カ月にわたる詳細な検証によって、
最終的に解決されました。」
とかかれているようですが、先日
「未だに証明はされてません。現在、十五万乗まで証明されているのですが、
一般的な解決には達していないようです。2007年9月13日までに
この定理を証明した人には”賞金10万マルク”を与えるとドイツの数学者ウォルスケールは発表してます。
コレ真面だそうです。」

 E-mail
E-mail
 戻る
戻る