Weekend Mathematics乛僐儘僉僂儉幒乛1999.4乣6乛NO.53
僐儘僉僂儉幒
NO.446丂丂丂丂'99 4/21 丂丂 悈偺棳傟 丂丂丂 價僼僅儞偺恓偺幚尡乮俀乯
丂丂
倫亖俀倠乛兾倓偲側傞偙偲傪徹柧偟傑偟傚偆丅
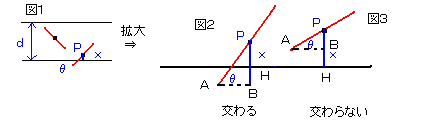 亙峫偊曽亜
亙峫偊曽亜
侾杮偺恓傪擟堄偵彴偵棊偲偟偨偲偒偺恾侾傪尒偰偔偩偝偄丅
恓偑暯峴慄偲岎傢傞偲偟偨傜丄恓偺拞揰俹偐傜嵟傕嬤偄暯峴慄偺侾杮偲岎傢傞丅
恓偺拞揰俹偲暯峴慄偺偆偪偺堦斣嬤偄捈慄偲偺嫍棧傪倶偲偟丄
恓偲偦偺暯峴慄偺側偡妏傪兤偲偍偔丅乮恾俀嶲徠乯
丂
偙偺偲偒丄曄悢倶丄兤偺曄堟偼丄侽亝兤亙兾丄侽亝倶亝倓乛俀乧乮仏乯丂偱偁傞丅
嵗昗暯柺忋偵丄曄堟乮仏乯傪恾帵偟丄傑偨丄恓偑捈慄偲岎傢傞兤偲倶偵娭偡傞忦審傪
媮傔丄偦傟傪嵗昗暯柺偵恾帵偟丄椉幰偺柺愊斾傪媮傔傞丅
側偍丄恓偺抂揰偑暯峴慄忋偵偁傞応崌偼乽岎傢偭偰偄傞乿傕偺偲偟偰埖偭偰傕
乽岎傢偭偰偄側偄乿偲偟偰埖偭偰傕寢壥偼摨偠偱偁傞丅
偙偙偱偼丄乽岎傢偭偰偄傞乿傕偺偲偟偰埖偆偙偲偵偡傞丅
丂
 亂夝摎亃偨偩偟丄倓亞倠偺応崌傪峫偊傑偡丅
亂夝摎亃偨偩偟丄倓亞倠偺応崌傪峫偊傑偡丅
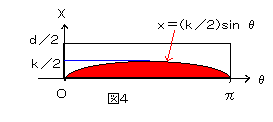
恓偑暯峴慄偺侾偮偲岎傢傞忦審偲偼丄恓偺拞揰偐傜堦斣嬤偄暯峴慄偲岎傢傞偙偲偱偁傞丅
恾俀傪尒偰壓偝偄丅
恓偑堦斣嬤偄暯峴慄偲岎傢傞曽偺抂揰傪俙丄拞揰傪俹丄揰俹偐傜堦斣嬤偄暯峴慄偵悅慄俹俫傪堷偔丅
傑偨丄俙傪捠傝暯峴慄傪堷偒丄悅慄俹俫偲偺岎揰傪俛偲偍偔丅
偝傜偵丄佢俹俙俛亖兤丂偲偍偔丅
偡傞偲丄俹俙亖倠乛俀丆俹俛亖乮倠乛俀乯亊倱倝値兤
偟偨偑偭偰丄倶偲俹俛偺娭學傛傝丄岎傢傞忦審偼丂倶亝乮倠乛俀乯亊倱倝値兤
岎傢傜側偄忦審偼丂倶亜乮倠乛俀乯亊倱倝値兤丂偱偁傞丅亙恾俁傪嶲徠亜
傛偭偰丄岎傢傞忦審傪嵗昗暯柺偱彂偔偲丄恾係偵側傝傑偡丅
偟偨偑偭偰丄媮傔傞妋棪倫偼


NO.447丂丂丂丂'99 4/21 丂丂 悈偺棳傟 丂丂丂 僆僀儔乕偺乽柍尷夝愅擖栧乮侾乯乿乮俁乯
丂丂
僆僀儔乕偺乽柍尷夝愅擖栧乮侾乯乿戞俀栭偺巒傑傝丄巒傑傝丅
愭擔丄僛乕僞乕娭悢兡乮俀乯暔岅偱彂偒傑偟偨偑丄僆僀儔乕偼侾俈俁俆擭偵丄
兡乮俀乯丆兡乮係乯丆丒丒丒傪媮傔傑偟偨丅
偦偺屻丄尋媶偼摉慠懕偄偰丄侾俈係俋擭偵丄兡乮侽乯丆兡乮亅侾乯丆兡乮亅俀乯丆丒丒丒丆
兡乮倱乯偲兡乮侾亅倱乯偺娭學傪敪尒偟偰偄傑偡丅
傕偆堦搙偙偺慺惏傜偟偄岞幃傪彂偒傑偡丅
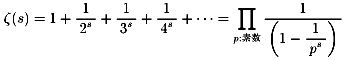
僛乕僞乕娭悢兡乮倱乯偺慺惏傜偟偄偺偼倱偵偳傫側暋慺悢傪戙擖偟偰傕丄
堄枴傪帩偮偲偄偆揰偱偡丅
亙悢妛揑偵偼乽夝愅愙懕壜擻乿偲尵偄傑偡亜
僆僀儔乕偺尒偮偗偨宍乮侾俈係俋擭乯偱尵偄傑偡偲丄
倱亝侽偺偲偒丄寧栭偺悽奅
侽亝倱亝侾偺偲偒丄偨偦偑傟偲偒亙梉從偗丒挬從偗亜
侾亝倱偺偲偒丄拫娫懢梲偺悽奅
丂偲儐僯乕僋側寧偺儅乕僋偲懢梲偺儅乕僋傪彂偄偰偄傑偡丅
摿偵丄寧栭偺悽奅偱偺寁嶼偑晄巚媍側寢壥偵側傝傑偡丅
堦椺傪嫇偘傑偡偲丄
兡乮侽乯亖侾亄侾亄侾亄丒丒丒亖亅侾乛俀
兡乮亅侾乯亖侾亄俀亄俁亄係亄丒丒丒亖亅侾乛侾俀
兡乮亅俀乯亖侾亄係亄俋亄侾俇亄丒丒丒亖侽
兡乮亅俁乯亖侾亄俉亄俀俈亄俇係亄丒丒丒亖侾乛侾俀侽
偙傟傜偼堦懱壗傪堄枴偟偰偄傞偺偱偟傚偆偐丠
傕偪傠傫晛捠偵偼偙傟傜偼柍尷戝偵側偭偰偄傞偼偢偱偡丅
偙偺寁嶼偼寁嶼偺払恖偱偁傞僆僀儔乕偑
俀俆侽擭慜偵傗偭偨寁嶼偱偡丅
師夞丄偙偺寁嶼傪僆僀儔乕偵側傝戙傢偭偰
僐儘僉僂儉幒偺co-worker偝傫偲偛堦弿偵峴偭偰傒傑偟傚偆丅
偦偙偱丄崱栭偺廻戣偱偡丅
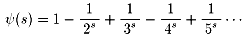
偲偍偄偰丄冋乮倱乯偲兡乮倱乯偺娭學傪敪尒偟偰偔偩偝偄丅

NO.448丂丂丂丂'99 4/23 丂丂 昹揷丂柧枻 丂丂丂嶰妏宍偺妋棪乮俀乯
丂丂
俻俛俙俽俬俠偺僾儘僌儔儉傪嶌惉偟媮傔傑偟偨丏撪梕偼師偺捠傝偱偡丏
墌偺敿宎傪侾偲偟傑偡丏棎悢偵傛傝丆侽偐傜俀兾傑偱偺妏倲傪俁屄媮傔丆
嶰妏宍偺俁捀揰偺嵗昗乮倶(倞),倷(倞)乯傪媮傔傑偡丏
師偵俁曈偺挿偝倓(倞)傪媮傔丆嵟戝曈倓倣倎倶傪媮傔傑偡丏
嵟戝曈偵懳偡傞妏偑嵟戝妏偱偡偐傜丆偙偺妏偺僐僒僀儞傪媮傔丆
偦偺晞崋傪媮傔傑偡丏
偙傟偵傛傝捈妏丆塻妏丆撦妏嶰妏宍偺偄偢傟偵側傞偐偑暘偐傝傑偡丏
偙偺帋峴傪侾侽侽侽侽侽侽乮倣倎倶乯夞孞傝曉偟丆偦傟偧傟偺妋棪傪媮傔傑偡丏
偙偺僾儘僌儔儉偵傛傝丆妋棪偼
- 侽
- 侽.俀係俋俈俋侽
- 侽.俈俆侽俀侾侽
偲側傝傑偟偨丏
幚嵺偵偼丆
- 侽
- 侽.俀俆
- 侽.俈俆
偲側傞偺偱偟傚偆丏
'sankaku.qb
pi = 3.14159
RANDOMIZE TIMER
DIM x(2), y(2), d(2), kaisuu(2)
FOR j = 0 TO 2
kaisuu(j) = 0
NEXT
shikoukaisuu = 0
max = 1000000
CLS
WHILE INKEY$ = "" AND shikoukaisuu < max
shikoukaisuu = shikoukaisuu + 1
FOR j = 0 TO 2
t = 2 * pi * RND
x(j) = COS(t)
y(j) = SIN(t)
NEXT
FOR j = 0 TO 2
j1 = (j + 1) MOD 3
j2 = (j1 + 1) MOD 3
d(j) = SQR((x(j2) - x(j1)) * (x(j2) - x(j1)) + (y(j2) - y(j1)) * (y(j2) - y(j1)))
NEXT
dmax = d(0)
jmax = 0
FOR j = 1 TO 2
IF d(j) > dmax THEN
dmax = d(j)
jmax = j
END IF
NEXT
j1 = (jmax + 1) MOD 3
j2 = (j1 + 1) MOD 3
cosine = (d(j1) * d(j1) + d(j2) * d(j2) - d(jmax) * d(jmax)) / (2 * d(j1) * d(j2))
bangou = -(cosine > 0) - 2 * (cosine < 0)
kaisuu(bangou) = kaisuu(bangou) + 1
LOCATE 1, 1
FOR j = 0 TO 2
PRINT USING "####### ####### / ####### =##.######"; j + 1; kaisuu(j); shikoukaisuu; kaisuu(j) / shikoukaisuu
NEXT
WEND
WHILE INKEY$ <> ""
WEND
END

NO.449丂丂丂丂'99 4/24 丂丂 Junko 丂丂丂嶰妏宍偺妋棪乮俁乯
丂丂
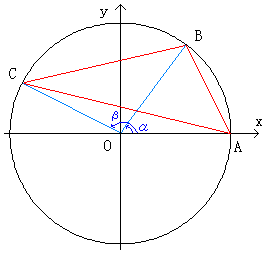 扨埵墌廃忋偵俁揰俙俛俠傪偲偭偰嶰妏宍傪嶌傝傑偡丅
扨埵墌廃忋偵俁揰俙俛俠傪偲偭偰嶰妏宍傪嶌傝傑偡丅
揰俙(侾丆侽)偲偟傑偡丅
俷俛丄俷俠偺曃妏傪偦傟偧傟兛丄兝偲偟丄兛亙兝偲偟傑偡丅
撦妏嶰妏宍偺応崌傪師偺俁偮偺働亅僗偵暘偗偰挷傋傑偡丅
侾丏佢俛偑撦妏偺偲偒丄
佢俛亖兾亅(1/2)兝亜(1/2)兾
廬偭偰丄兾亜兝
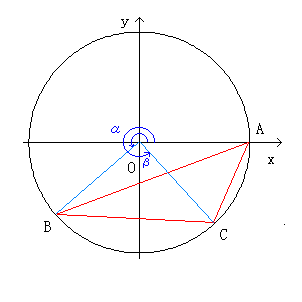 俀丏佢俠偑撦妏偺偲偒丄
俀丏佢俠偑撦妏偺偲偒丄
佢俠亖(1/2)兛亜(1/2)兾
廬偭偰丄兛亜兾
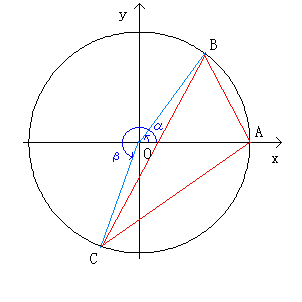 俁丏佢俙偑撦妏偺偲偒丄
俁丏佢俙偑撦妏偺偲偒丄
佢俙亖(1/2)(兝亅兛)亜(1/2)兾
廬偭偰丄兝亜兾亄兛
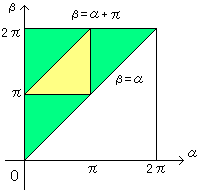
埲忋傪憤崌偡傞偲丄撦妏嶰妏宍偵側傞偺偼嵍恾偺墿椢偺晹暘偵側傝傑偡丅
慡帠徾(婲偙傝偆傞偡傋偰偺働亅僗)偼丄捈慄兛亖侽丄兝亖俀兾丄兝亖兛
偱埻傑傟偨嶰妏宍偵側傝傑偡丅嫬奅慄偼娷傒傑偣傫丅
廬偭偰丄撦妏嶰妏宍偵側傞妋棪偼丄柺愊斾偱3/4偲側傝傑偡丅
捈妏嶰妏宍偵側傞偺偼丄兛亖兾丄兝亖兾丄兝亖兾亄兛偺偲偒側偺偱丄
嵍恾偺墿椢偲墿怓偺嫬奅慄偵側傝傑偡丅柺愊偼侽偱偡偺偱丄妋棪0
巆傝偺墿怓偺晹暘偑塻妏嶰妏宍偲偄偆偙偲偵側傝丄柺愊斾偵傛傝1/4偲側傝傑偡丅

NO.450丂丂丂丂'99 4/25 丂丂 悈偺棳傟 丂丂丂 嶰妏宍壜擻側妋棪乮侾乯
丂丂
戞侾係夞悢妛揑側墳曞栤戣
懢榊偝傫偺偍巕偝傫偼岺嶌偑戝岲偒偱偡丅
嵶挿偄朹偑侾杮偁傝傑偡丅
偦傟傪俀僇強偱愜偭偰丄俁杮偵暘偗傑偡丅
偙偺偲偒丄弌棃偨俁杮偱嶰妏宍傪嶌傟傞妋棪傪媮傔偰偔偩偝偄丅
偨偩偟丄朹傪愜傞埵抲偼偳偺揰偱傕摨偠偲偡傞丅
懢榊偝傫傕摱怱偵偐偊偭偰丄偄傠偄傠偲愜偭偰峫偊傞偙偲偵偟傑偟偨丅
奆偝傫傕丄峫偊偰偔偩偝偄丅
丂
亙栤戣偺弌揟丗嶼悢偼傾僞儅偺傛偔側傞僷僘儖偩丗傒偔偵弌斉亜丂

NO.451丂丂丂丂'99 4/26 丂丂 悈偺棳傟 丂丂丂 僆僀儔乕側傜丠
丂丂
丂僆僀儔乕偺嬈愌傪挷傋偰偄偰丄師偺晄掕愊暘傗旝暘傪僆僀儔乕側傜
偳傫側夝朄偱偟偨偩傠偆偹丅

僆僀儔乕偺棫応偵側偭偰儐僯乕僋側夝朄傪偍婑偣壓偝偄丅

NO.452丂丂丂丂'99 4/28 丂丂 Junko 丂丂丂 僆僀儔乕偺乽柍尷夝愅擖栧乮侾乯乿乮係乯
丂丂
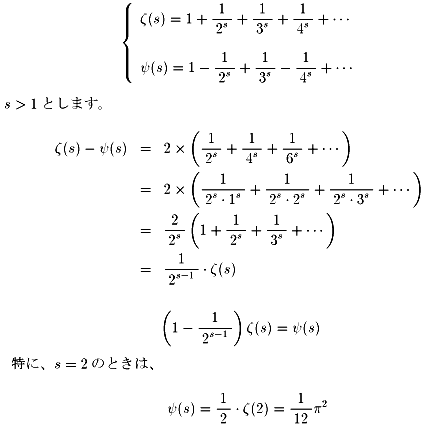

NO.453丂丂丂丂'99 4/29 丂丂 悈偺棳傟 丂丂丂 僆僀儔乕偺乽柍尷夝愅擖栧乮侾乯乿乮俆乯
丂丂
奆偝傫両僛乕僞乕娭悢暔岅偺懕曇偱丄僆僀儔乕偺亀柍尷夝愅擖栧乮侾乯亁
偺戞俁栭偺巒傑傝丄巒傑傝丅
慜栭偺廻戣傕丄忋庤偵夝偗偰偄傑偡偹丅
偙傟偐傜傕丄偙偺挷巕偱傛傠偟偔偹丅
偝偰丄冋乮倱乯偲兡乮倱乯偺娭學偼
冋乮倱乯亖乮侾亅俀(侾亅倱)乯兡乮倱乯丂傛傝
冋乮侽乯亖亅兡乮侽乯丂
冋乮亅侾乯亖亅俁兡乮亅侾乯丂
冋乮亅俀乯亖亅俈兡乮亅俀乯丂
冋乮亅俁乯亖亅侾俆兡乮亅俁乯丒丒丒丒丒丒
偲側傝傑偡丅偟偨偑偭偰丄
侾亄侾亄侾亄丒丒丒亖兡乮侽乯亖亅冋乮侽乯
侾亄俀亄俁亄係亄丒丒丒亖兡乮亅侾乯亖亅侾乛俁丒冋乮亅侾乯
侾亄係亄俋亄侾俇亄丒丒丒亖兡乮亅俀乯亖亅侾乛俈丒冋乮亅俀乯
侾亄俉亄俀俈亄俇係亄丒丒丒亖兡乮亅俁乯亖亅侾乛侾俆丒冋乮亅俁乯
丒丒丒丒丒丒偑摼傜傟傑偡丅
偦偙偱丄崱栭偼冋乮侽乯丆冋乮亅侾乯丆冋乮亅侾乯丆冋乮亅俁乯丆丒丒丒
傪寁嶼偟傑偡丅
偦偺慜偵丄師偺摍幃傪巚偄偩偟偰偔偩偝偄丅
侾亄倶亄倶俀亄倶俁亄倶係亄丒丒丒亖侾乛(侾亅倶)丒丒丒嘆
偪傚偭偲丄婋側偄寁嶼偱偡偑丄偙偙偱丄倶亖亅侾傪戙擖偟偰偔偩偝偄丅
摉慠丄廂懇忦審偵偁偭偰偄傑偣傫両
偱傕丄偙偙偺偲偙傠傪夝愅愙懕偲偄偆庤朄偱堄枴偯偗偨偺偑
僆僀儔乕偺侾侽侽擭屻偺儕乕儅儞偱偟偨丅
奆偝傫丄偙偺傛偆偵峫偊偰偔偩偝偄丅偡傞偲丄
冋乮侽乯亖侾亅侾亄侾亅侾亄丒丒丒亖侾乛俀偲媮傑傝丄
兡乮侽乯亖侾亄侾亄侾亄侾亄丒丒丒亖亅侾乛俀偑偱偰偒傑偡丅
偙偙偱丄崱栭偺廻戣偱偡丅
摍幃嘆偺椉曈傪俀忔偟偰丄冋乮亅侾乯偐傜丄
兡乮亅侾乯亖侾亄俀亄俁亄係亄丒丒丒傪媮傔偰偔偩偝偄丅
傑偨丄帪娫揑偵梋椡偺偁傞恖偼丄
冋乮亅俀乯丄冋乮亅俁乯偵傕僠儍儗儞僕偟偰傕椙偄偱偡傛丅
撉幰偺奆偝傫偵丄傕偆堦搙尵偭偰偍偒傑偡丅
偙偙偱偺寁嶼偼僆僀儔乕偑敪尒偟偨兡乮倱乯偲兡乮侾亅倱乯偺乽憃懳惈乿
偺棟夝傪栚揑偵偟偰偄傞偙偲傪両
偦傟偱偼丄戞俁栭偺枊傪壓傠偟傑偡丅
傑偨丄柧擔偺栭偍夛偄偟傑偟傚偆丅

 E-mail
E-mail
 栠傞
栠傞
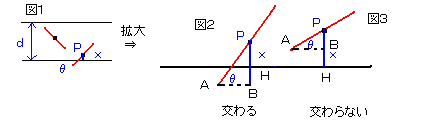 亙峫偊曽亜
亙峫偊曽亜 亂夝摎亃偨偩偟丄倓亞倠偺応崌傪峫偊傑偡丅
亂夝摎亃偨偩偟丄倓亞倠偺応崌傪峫偊傑偡丅

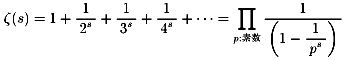
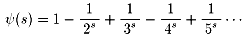
 扨埵墌廃忋偵俁揰俙俛俠傪偲偭偰嶰妏宍傪嶌傝傑偡丅
扨埵墌廃忋偵俁揰俙俛俠傪偲偭偰嶰妏宍傪嶌傝傑偡丅 俀丏佢俠偑撦妏偺偲偒丄
俀丏佢俠偑撦妏偺偲偒丄 俁丏佢俙偑撦妏偺偲偒丄
俁丏佢俙偑撦妏偺偲偒丄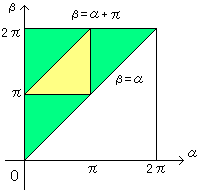

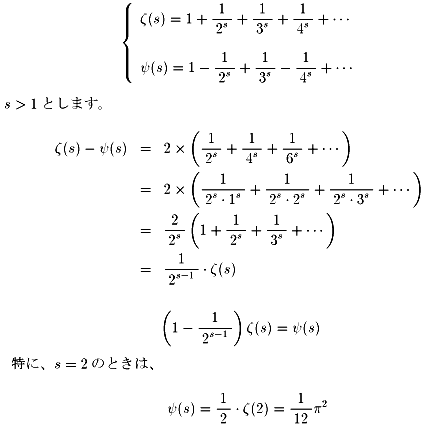
 E-mail
E-mail
 栠傞
栠傞