
Weekend Mathematics/コロキウム室/1999.1~3/NO.39
NO.315 '99 2/1 浜田 明巳 1999!の桁数(3)
1999!を実際に計算するプログラム(昔懐かしいN88BASIC)
を作ってみました。
このプログラムにより、確かに桁数は5733桁、
0が並ぶのは確かに496桁であることがわかります。
100 'SAVE"1999K.BAS",A
110 MITSUMORI=5000:DEFDBL A:CLS 3
120 DIM A(MITSUMORI):A(1)=1:FOR J=2 TO MITSUMORI:A(J)=0:NEXT:KETA3=1
130 FOR J=2 TO 1999:LOCATE 0,0:PRINT J;"!を計算中"
140 FOR JJ=1 TO KETA3:A(JJ)=A(JJ)*J:NEXT
150 KARINOKETA3=KETA3
160 FOR JJ=1 TO KETA3+1
170 IF A(JJ)>=1000 THEN A(JJ+1)=A(JJ+1)+INT(A(JJ)/1000):A(JJ)=A(JJ)-1000*INT(A(JJ)/1000):IF JJ>=KETA3 THEN KARINOKETA3=KARINOKETA3+1
180 NEXT
190 KETA3=KARINOKETA3
200 NEXT
210 FOR J=KETA3 TO 1 STEP -1:A$=RIGHT$(STR$(A(J)),LEN(STR$(A(J)))-1)
220 IF J=KETA3 THEN KOTAE$=A$ ELSE KOTAE$=KOTAE$+","+RIGHT$("00"+A$,3)
230 NEXT:PRINT
240 OPEN"1999.DAT" FOR OUTPUT AS #1:WRITE #1,KOTAE$:CLOSE
250 END
165,813,754,622,531,662,058,769,669,028,816,201,914,055,860,405,289,019,728,596,771,853,019,038,952,800,411,200,136,615,429,866,296,127,701,176,470,612,917,054,629,042,408,707,646,898,065,693,316,763,171,844,452,817,029,278,081,970,302,558,626,285,935,323,928,196,772,022,702,621,978,733,518,837,054,361,485,217,342,079,171,876,215,790,438,766,822,563,743,997,718,429,623,704,016,204,473,280,753,616,625,326,398,827,878,589,835,768,359,344,679,528,056,407,935,800,858,616,328,578,055,002,107,006,210,216,921,286,856,350,087,941,773,898,449,960,641,764,498,332,926,702,789,927,451,828,683,175,066,693,275,200,586,006,076,317,744,019,134,076,076,123,460,497,603,015,782,209,282,740,337,973,248,525,776,144,102,617,449,997,863,225,407,032,768,339,484,766,050,733,811,335,666,013,415,776,102,597,247,230,809,119,637,602,013,264,861,315,751,287,376,024,148,032,375,463,697,082,928,141,765,889,787,241,438,157,298,225,186,995,663,667,088,631,804,426,245,046,753,310,805,072,229,854,706,353,910,656
,866,281,915,786,151,009,974,957,479,158,235,471,387,236,935,163,992,774,837,149,304,419,688,163,412,076,239,417,193,734,797,914,628,870,287,269,918,750,792,907,734,068,147,108,974,986,199,906,799,740,508,278,281,938,017,113,656,456,125,192,354,936,454,813,311,230,985,538,302,965,775,100,947,567,791,582,678,935,746,145,458,389,524,851,123,547,305,968,803,892,582,555,342,216,127,952,824,368,133,265,188,692,325,195,394,024,762,300,356,274,701,307,283,036,127,068,151,377,456,835,791,703,048,915,537,472,641,108,745,390,673,854,846,620,778,055,669,914,025,679,300,345,297,309,982,628,655,370,588,540,759,961,282,258,389,285,729,028,301,092,827,380,476,188,731,508,339,711,244,222,242,899,174,900,774,016,310,414,945,482,928,690,875,944,309,688,346,414,139,944,226,792,319,948,297,106,976,492,232,645,546,004,551,855,023,074,724,957,914,294,025,380,933,962,473,192,590,439,937,256,445,704,009,670,037,312,960,028,549,364,789,299,821,825,327,947,806,205,115,509,345,278,030,154,391,814,555,25
2,800,622,954,499,191,705,399,683,951,026,038,429,334,591,738,953,279,272,350,074,346,328,462,315,966,668,806,214,048,710,033,586,423,180,969,624,849,314,234,359,996,725,196,944,683,635,243,563,586,367,280,850,177,433,738,754,551,477,761,976,773,970,553,710,956,650,678,409,770,545,970,731,383,208,771,080,793,812,631,429,044,900,611,221,945,124,338,591,027,479,707,875,995,850,635,883,785,893,747,930,809,832,965,939,427,570,917,891,046,300,741,035,888,665,867,698,017,152,484,541,035,294,979,350,690,990,406,517,795,080,381,454,194,287,280,644,108,849,068,091,241,788,369,609,151,559,207,359,566,993,446,421,172,000,389,623,345,604,883,365,825,716,747,218,736,617,818,286,024,422,239,165,927,470,846,515,062,265,838,116,372,683,939,661,423,736,912,242,546,141,569,976,254,866,252,989,563,515,523,841,800,740,595,551,114,626,686,348,846,911,835,028,782,806,200,145,288,021,926,426,451,468,803,239,766,729,089,833,061,919,802,631,274,553,593,331,934,677,383,054,227,523,099,051,042,025,317,9
13,838,263,294,746,196,624,759,842,977,085,836,209,664,765,341,836,747,772,002,293,179,919,080,521,529,724,913,313,765,302,711,790,377,947,054,139,440,213,912,975,544,940,317,705,283,958,975,487,008,890,344,391,434,905,109,505,450,074,176,030,844,441,860,125,155,332,961,034,300,741,824,915,266,391,044,131,768,279,021,802,843,390,642,084,608,566,523,570,588,156,087,947,888,561,318,792,376,561,758,615,495,274,914,605,067,343,652,102,949,007,209,031,937,691,332,084,948,852,118,879,703,140,438,626,851,132,713,265,290,431,189,650,711,337,910,593,571,751,459,318,818,170,150,086,625,909,131,038,019,873,684,797,601,321,316,182,072,723,425,556,713,601,075,229,191,925,505,068,470,656,517,428,110,958,315,811,946,316,382,907,677,505,638,153,912,529,984,579,412,266,728,717,718,931,841,586,865,336,648,294,677,599,847,229,118,436,754,415,139,328,850,439,874,944,996,171,777,783,120,341,417,381,892,342,591,922,486,824,436,976,237,551,612,111,055,280,600,647,914,828,595,684,054,346,912,737,882,
059,443,439,673,362,595,623,096,075,572,369,418,134,795,821,836,245,035,826,714,114,076,330,623,900,231,961,272,472,585,181,861,813,970,378,892,271,045,524,152,730,828,095,311,087,143,490,801,486,662,023,260,100,996,406,927,441,340,975,503,641,434,850,535,368,750,463,833,243,751,087,387,686,371,175,754,374,123,360,137,085,015,790,561,402,948,089,061,080,373,718,973,755,475,310,469,278,337,290,626,259,188,341,078,856,403,930,749,627,938,066,176,475,211,173,193,939,477,425,442,882,233,068,145,197,063,832,989,022,101,046,140,668,993,557,950,448,132,439,471,206,605,227,462,501,783,335,316,454,720,789,686,493,371,710,735,253,606,794,466,009,790,361,532,390,749,214,761,297,794,506,377,411,985,886,662,861,455,162,880,464,895,366,649,772,528,194,181,320,237,325,122,540,404,734,558,036,316,043,747,071,986,500,352,055,709,297,765,139,413,678,827,409,591,001,224,848,880,555,673,159,097,641,380,795,482,094,895,479,058,669,313,603,044,455,216,472,622,489,267,573,507,056,221,071,527,743,044
,819,789,189,173,662,661,797,881,645,719,462,644,196,993,128,136,621,431,387,781,570,231,915,194,584,210,816,556,722,818,154,785,982,989,233,169,275,746,158,098,167,837,677,569,201,712,902,081,459,918,911,133,454,760,885,076,587,669,365,142,305,420,943,277,069,164,585,975,666,058,947,864,270,831,042,411,841,408,966,256,465,618,760,770,963,485,134,851,649,738,821,911,693,241,504,435,765,186,702,833,191,934,147,044,243,865,360,881,134,424,511,542,467,330,597,130,090,136,306,901,054,002,539,107,870,503,027,424,100,673,929,789,051,385,353,890,327,756,386,270,250,837,166,198,033,126,608,207,502,404,386,201,523,805,964,516,105,077,192,676,569,342,769,243,212,785,395,397,670,588,259,785,594,341,869,940,341,947,896,371,874,841,749,071,461,646,098,154,888,545,071,968,421,827,666,679,653,910,090,656,496,727,512,103,022,281,670,289,303,481,235,980,752,801,697,449,761,660,900,217,179,983,628,311,963,598,217,701,436,027,737,506,039,927,165,985,337,398,656,563,406,761,826,872,042,831,131,60
3,384,418,792,566,391,448,126,166,642,170,906,488,812,348,539,771,718,001,746,171,579,619,837,381,819,456,057,642,703,328,891,823,106,955,623,723,525,627,613,171,350,619,763,509,063,522,745,824,022,966,124,054,429,337,300,476,153,396,587,983,877,790,505,839,970,002,624,903,151,881,570,672,206,134,518,517,493,677,899,958,004,629,624,037,526,242,770,784,133,140,880,407,723,154,152,703,338,706,315,062,220,932,102,054,186,559,546,565,000,577,235,280,138,886,862,189,033,594,449,885,425,528,363,638,390,623,599,416,428,847,922,108,794,447,580,233,934,102,405,005,023,908,231,179,110,419,266,244,067,135,417,039,934,243,316,081,360,104,411,654,363,909,542,689,422,734,565,778,010,864,436,560,953,696,982,604,630,114,550,738,763,540,465,432,682,489,929,277,005,288,725,139,644,907,301,844,215,910,754,318,623,108,483,936,141,084,673,685,299,643,138,556,223,845,460,451,494,160,083,415,085,136,710,129,882,835,854,931,655,608,174,751,085,632,213,413,559,825,132,027,114,115,879,815,437,237,650,9
23,597,047,762,131,705,749,234,754,036,695,040,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000

NO.316 '99 2/1 Junko 「オイラ-の贈物」
「月の光」さん曰く、
高校3年の初めにオイラーの公式とであって数学に興味を持ち、 図書館で見つけたこの本を読んでみました。この本というのは、「オイラ-の贈物」(吉田武著、海鳴社、\3000)です。
内容は丁寧で読みやすく、n次方程式の判別式や、 フィボナッチ数列の積表示などが有ります。
そこで読んでやってみたテイラー展開とフーリエ級数に 強い感動を覚えました。
「人類の至宝eiπ=-1を学ぶ」という副題がついていますが、
まさにその通りです。
eiπ=-1というのは、
オイラ-の公式
eiθ=cosθ+i sinθで、θ=πとしたものです。
この公式の周辺に関わる内容が分野を問わず出てきます。
数学のあらゆる分野がこの公式を通して1つにつながっていくようです。
オイラ-の公式がいかに重要かつ偉大であるかを痛感させられます。
数学を勉強していると、
時々自分の視界が急に開ける感動を味わうことができます。
今回も、そんな感動を経験しました。

NO.317 '99 2/1 水の流れ 2円の交点を通る直線(1)
太郎さんには、高校に通っているお子さんがいます。
ある日、お子さんに
「2円:x2+y2=1 ・・・・・・①
x2+y2-6x-4y+9=0・・・・・・②
の交点を通る直線の方程式を求めよ。」
という問題を質問されました。
太郎さんは、①から②を引いて、
答え 3x+2y=5 と言ってにっこりしました。
ところが、お子さんは、
「でも、お父さん、この2円を座標平面上で
書くと交わらないのだけど、一体どんな直線なの?」
と言われてしまいました。
太郎さんに変わって、誰か教えてください。
この種の問題は当然、2円の交点が有る場合を扱っていますが、
ないとき、直線式だけは出てきます。
この直線は一体何なのでしょうか。
疑問に思ったことはありませんか?
<追加とお詫び 2/4>
NO317の2円の交点を通る直線に関して、「数学セミナ-2月号」を読んで、
上のような問題を見かけましたので、コロキウム室で取り上げて頂こう
と思いました。
ここに、関係に人達に多大な迷惑をおかけしましたことを、
ここに、深くお詫びいます。

NO.318 '99 2/1 (2/7内容追加) 水の流れ 1998倍数の問題(4)
最近、読んだ理系への数学=2月号に依然扱った問題の別証がありましたので、 ご紹介します。
2つの自然数m、nについての数学的帰納法を紹介します。
2つの自然数m、nについての命題P(m、n)について、
【Ⅰ】命題P(1,n)は、常に正しい。
【Ⅱ】命題P(m、1)は、常に正しい。
【Ⅲ】命題P(m、n+1)、P(m+1,n)が、ともに正しいとき、
命題P(m+1,n+1)も正しい。
ならば、すべての自然数m、nに対して、
命題P(m+1,n+1)は正しい。
<平面上で、格子点を考えてください。この証明方法が理解し易いです>
NO.184の3.
「n個の連続した自然数の積は、n!で割る切れることを示せ。」
<証明> n個の連続した自然数の積を
P(m、n)=m(m+1)(m+2)・・・(m+n-1)とおく。
【Ⅰ】 m=1のとき、
P(1,n)=1・2・3・ ・・・ ・n=n! となり、明らかに、
n!の倍数である。
【Ⅱ】 n=1のとき、 P(m、1)=m となり、
明らかに、1!の倍数である。
【Ⅲ】P(m、n+1)は、(n+1)!の倍数、
P(m+1,n)は、n!の倍数 であると、2つ仮定する
ここで、 P(m+1,n+1)を考えると、
P(m+1,n+1)=(m+1)(m+2)・・・(m+n){m+(n+1)}
=m(m+1)(m+2)・・・(m+n)
+(m+1)(m+2)・・・(m+n)(n+1)
=P(m,n+1)+P(m+1,n)(n+1)
これは、明らかに、(n+1)!の倍数であることを示している。
NO.319 '99 2/1 Junko 2円の交点を通る直線(2)
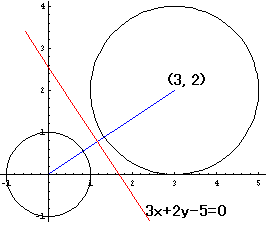
確かに、2つの円の交点が存在すれば、それは
x2+y2=1 ・・・・・・①と
x2+y2-6x-4y+9=0・・・・・・②を
満たしますから、
それらの差をとった式、3x+2y=5・・・・・・③をも満たします。
しかしそれは、2つの円の交点が存在すれば、の話しです。
この場合、③を変形した y=(5-3x)/2を①に代入してできる2次方程式
13x2-30x+21=0の判別式
D/4=152-13・21=-48<0より、
交点は存在しません。
では一体、3x+2y=5・・・・・・③は何を意味するのでしょうか?
2つの円の中心を結ぶ直線に対して垂直な直線で、これらは
2つの円の外側の部分で交わるようです。

NO.320 '99 2/2 水の流れ 算数・数学甲子園
我が岐阜県出身の偉大な世界的に有名な数学者故「高木貞治」
先生にになんで、この1月7日に出身地の同県本巣郡糸貫町で開催された
第1回「算数・数学甲子園」というイベントを紹介します。
これは、数学の楽しさに触れて子供達に想像力を養うユニークな数学の問題
に、町内の小・中学生83人が挑戦したコンクールのことです。
このときの、開催の案内をお知らせします。
日時:平成11年1月7日(木)午前9時から10時30分
場所:同内の福祉センター
持ち物:筆記用具・参加費200円
結果の発表:後日学校へ賞状と賞品を送ります。
高木貞治先生の業績の大要
(1875年生まれ、1960年84歳で生涯を終える)
東京帝国大学理科大学教授を務めつつ、明治・大正期に国際的に全く無視
されていた日本の数学のレベルを、その巨大で秀麗な類体論という一理論を
想像することによって、世界的なレベルに押し上げた大数学者です。
類体論とは相対アーベル体の理論のことで、この応用として、応用として
「クロネッカーの青春の夢」という難問を完全に解決させました。
著書には、有名な本が一杯あります。
高木先生は岐阜県で誇れる偉大な数学者です。
糸貫町には記念館もありますので、機会があれば、見学したいです。

NO.321 '99 2/2 水の流れ 「数の悪魔」
<こんな妖精=悪魔に逢いたい>
ハンス・マグヌス・エンツェンスベルガー(1929年生まれ)「著」
ロートラウト・ズザンネ・ベルナー(1948年生まれ) 「絵」
丘沢静也 東京都立大学教授(1947年生まれ)「訳」
A5版、257ページ、1998年9月発行、2840円 晶文社
エンツェンスベルガーという人はドイツを代表とする詩人、批評家、
評論から子供まで、 鋭く軽やかな想像力で多彩な文筆活動を続けている評論家です。
<この部分著作本引用>
全体を通して、数の悪魔を自称する年配で小柄な老紳士とロバートと
いう子供との中で、算数・数学が楽しくなる12夜にわたり、全編 会話調で書
かれています。この点、小生こと、<水の流れ>の授業編によく似ています。
著者は数学者ではないところに、
「算数って聞いただけで、じんましん出ちゃんだ」というロバートの子供の気持ちを
良く含んで、諭すようにおしゃべりを続けています。
もし、こんな悪魔、私は悪魔より妖精と言いたいが、毎日夜な夜な現れてくれるなら、
もっと、世界中の子供達から、算数・数学嫌いがなくなるように、思えます。
第1夜 数は1から始まり、どんな数だってそれに1を加えればもっと大きな 数になるんだよ。これが、数が無限にたくさんあることだよ。
第2夜 ローマ人は数字の記号に0を知らないまま生活していたが、うまく計 算出来ないところに、例えば、9+1の和にどうしても、10という0を必要と してきたんだよ。ここで、子供に10の1乗をポップと馴染みやすくしている。 10の3乗を3回ポップさせると言っている。
第3夜 素数の秘密に出会う。いわゆる数の神秘に等しい。私は学生時代に、 当時京都大学の「土井公二?」<もし、間違っていたら、何せ2十数年以上も前 にお会いした>先生の特別講義を聴講したことがあります。最後の講義終了後、 黒板に「数の神秘を知るために、あなたは青春をかけてみないか。」と黒板に書 かれたことを忘れない。だから、ときどき機会ある毎に、同じ言葉を無断で借用 しています。1例として、悪魔が4以上の偶数は二つの素数の和になるというゴ ールドバッハの未解決問題に頭を悩ませているのです。
第4夜 循環小数の神秘に出会う。 1例として、1=0.999999・・・・・・ これなど、私は生徒を引きつけるのに、いつも使っている手品みたいな数覚を 養うのに使っている。こでは、平方根のことを子供に平易に読まれやすく、大根 と呼んでいます。
第5夜 1,3,6,10,・・・という三角数の数列に触れている。 1例をあげると、隣り合う2つの三角数の和は平方数になる。 また、四角数、5角数、6角数にまで広げている。
第6夜 ここではフィボナッチ数列をウサギを例に分かり易く話している。
第7夜 サイコロを何個か準備して、パスカルの三角形を積み上げている。 ここでは、多くの性質を読者に伝えている。 私にとっても大変興味深いものが多かった。 心を引きつけさせたものに、順に斜めの数字の和がその1段下の右のサイコロの 数字には驚いた。三角数・四角数・五角数、・・・も並んでいる。 見方によって、フィボナッチ数列も発見出来る。 また、2.3,4,5,・・・の倍数に光をあてて、浮かび上がらせている。 クリスマスツリーの反対の逆三角形に光っている。 まさしく、神秘の光のようです。
第8夜 ロバートの通っている学校で、悪魔が先生で、黒板に向かって、順 列・組み合わせの授業をしている風景がでてくる。 ここで、階乗のことを、例えば4のびっくりは 4×3×2×1=24と呼んでいる。 当然、ここでも積み重ねられたパスカルの三角形のサイコロが でてきている。
第9夜 夢の中で、今まで扱ってきた数字が整列してきて、ロバートを悩まし ている。 天井には無限級数もでてきている。
第10夜 素晴らしい雪の結晶を眺めて、急にパソコンが登場してくる。 フィボナッチ数列の隣り合う2数に比が黄金比に近づくことも書いてあるし、多 面体のオイラーの定理まで悪魔が案内している。
第11夜 急流の中に大きな石があって、渡る切るのは大変なことをロバート に体験させている。数字のゴチャゴチャをすっきりさせる最高の方法はしかっり と眠ることなんだとも教えている。ここで、ロバートの好奇心はさらに燃え上が り、数と遊ぶだけでなく、どんなことがここに隠されているか、知りたくなって きていた。とうとう第12夜を向かえることになる。
第12夜 ロバートは夢をみることなく、悪魔とともにピタゴラスの宮殿に招 待される。 ここで、いろいろな悪魔に出会うことになります。
最後に、私達数学の先生はポッケル先生のように、子供がじんましんになるよう
な接しかたでなく、この本に出てくる数の悪魔=妖精のように、未だ見ぬ偉大な
数学者に話しかけたいです。本書は中学生から大人まで、おおぜいの人が数の不
思議に触れられる画期的な本です。皆さん、ご一読を!。

NO.322 '99 2/2 Junko 2円の交点を通る直線(3)

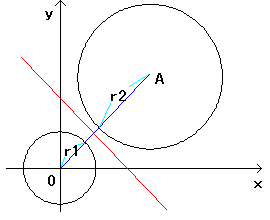
2つの円が離れている図を示しましたが、このことは 2つの円の位置関係によりません。
OAに垂直な直線となること、原点との距離については、
次のNO.323にて。

NO.323 '99 2/2 Junko 2円の交点を通る直線(4)


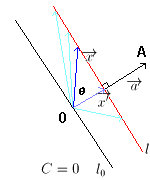

NO.324 '99 2/3 Idaho Potato 2円の交点を通る直線(5)
No.317の水の流れさんの問題について。
実は、これとそっくりの問題が、次の記事で扱われています。
答をばらしてしまうようですが、
記事の存在を知っている者としては、
それを紹介しないわけにはいきません。
岡部恒治・中村文則, 交わらない2円の交点を通る直線の存在, 数学セミナー, Vol.38(1999), 2月号, pp.2--5さらに、この記事の元ネタは、 北海道算数数学教育会・数学教育実践研究会のホームページ「数学のいずみ」 http://www.nikonet.or.jp/spring/ に掲載された文章とのことで、 「交わらない2円…」の問題に関する一連の議論のようすが、 このページに掲載されています。
そういうわけで、
「交わらない2円…」の問題に関する私自身のコメントは差し控えます。
ただ、件の数セミの記事のうち、
「1.受験数学は誰が作ったか」の一節を読んだときには、
私もNo.306で「テクニック偏重の受験数学」に対して批判的な見解を述べただけに、
うーむ、と考えさせられてしまいました。

 E-mail
E-mail
 戻る
戻る