NO.1894丂丂丂 僟僀僋僗僩儔朄偲椞堟擣幆丂丂丂丂2010.12.26.丂丂俢俢俿
奆偝傫丄僟僀僋僗僩儔朄偭偰偛懚抦偱偡偐丠丅抦傝傑偣傫傛偹丅抦偭偰偨傜儅僯傾夁偓傑偡^^丅僟僀僋僗僩儔朄偲偼丄摴楬僱僢僩儚乕僋偑梌偊傜傟偨帪偵丄偁傞岎嵎揰偐傜暿偺岎嵎揰偵偄偨傞嵟抁宱楬傪扵嶕偡傞昗弨揑乮屆揟揑乯曽朄偱偡丅庡偵岎捠寁夋暘栰偵偄傞妛惗偐島巘恮偟偐抦傜側偄偲巚偄傑偡丅僟僀僋僗僩儔偝傫偑1959擭偵採弌偟傑偟偨丅
摴楬僱僢僩儚乕僋偲偼丄恾-1偵傛偆側傕偺傪巜偟傑偡丅恾-1偼丄嶥杫傗嫗搒偺傛偆側岄斦偺栚偺巗奨抧偵懳墳偟偨丄摴楬僱僢僩儚乕僋偱偡丅
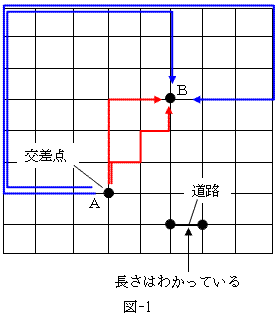 摴楬僱僢僩儚乕僋偱偼丄峫偊傞斖埻偺慡偰偺岎嵎揰偲丄堦偮偺岎嵎揰偵椬愙偡傞慡偰偺岎嵎揰偺僨乕僞丄偍傛傃椬傝崌偆岎嵎揰娫偺摴楬嫍棧偑梌偊傜傟傑偡丅
摴楬僱僢僩儚乕僋偱偼丄峫偊傞斖埻偺慡偰偺岎嵎揰偲丄堦偮偺岎嵎揰偵椬愙偡傞慡偰偺岎嵎揰偺僨乕僞丄偍傛傃椬傝崌偆岎嵎揰娫偺摴楬嫍棧偑梌偊傜傟傑偡丅
恾-1偺傛偆偵婯懃惈偺偁傞応崌偼丄椺偊偽揰乮岎嵎揰乯俙偐傜揰俛偵偄偨傞嵟抁宱楬乮愒乯偼丄(杒偵3僽儘僢僋丆搶偵2僽儘僢僋)恑傓擟堄偺宱楬偲偡偖傢偐傝傑偡偑丄僱僢僩儚乕僋偵婯懃惈偑側偄偲丄偦偆偼峴偒傑偣傫丅偄偒偍偄僩儔僀and僄儔乕偺扵嶕偲偄偆帠偵側傝傑偡丅
偡偖巚偄偮偔偺偼丄摴楬僱僢僩儚乕僋偺慡偰偺壜擻側捠傝曽傪懡暘栘偱慡扵嶕偟偰宱楬挿弴偵暲傋丄俙偐傜俛偵偄偨傞宱楬偩偗傪拪弌偟嵟抁傪慖傇偲偄偆傗傝曽偱偡丅堦偮偺岎嵎揰偵椬愙偡傞慡偰偺岎嵎揰偺僨乕僞偲丄椬傝崌偆岎嵎揰娫偺摴楬嫍棧偑梌偊傜傟傞偺偱丄偙傟偼尨棟揑偵偼壜擻偱偡丅偲偙傠偑彮偟奣嶼偡傞偲丄偙偺傗傝曽偼尰幚揑偵幚峴晄壜擻側偺偑傢偐傝傑偡丅
懡暘栘慡扵嶕傪恾-1偵帋偡偲偟傑偡丅岎嵎揰偼奣偹3暘栘偵側偭偰偄傑偡丅偡側傢偪丄偁傞摴楬偐傜岎嵎揰偵恑擖偟偨応崌丄3捠傝偺暘偐傟摴偲偄偆傢偗偱偡丅3捠傝偺撪偺堦偮傪慖傇偲丄傑偨3捠傝偺暘偐傟摴偑尰傟傑偡丅傕偟岎嵎揰偑100屄偁傞偲偡傟偽乮廲墶偵摴楬10杮乯丄挻奣嶼偱3亊3亊丒丒丒亊3亖3100偺扵嶕悢偵側傝傑偡丅
3100偼丄傎傏1050偺僆乕僟乕偱偡丅慜傕傗傝傑偟偨偑丄堦夞偺扵嶕傪1GHz偺CPU堦夞偺摦嶌偱姰椆偱偒傞偲偟偰傕丄1030擭傎偳偐偐傞寁嶼偵側傝傑偡丅傕偪傠傫1050屄偺拞偵偼丄摨偠僽儘僢僋傪偖傞偖傞弰夞偟偨傝丄俙偐傜弌敪偟側偐偭偨傝丄俛偵峴偐側偐偭偨傝丄捠夁宱楬偵栠偭偨傝偡傞偺傕偁傞偺偱丄惂栺忦審傪偮偗偰戝暆偵悢傪尭傜偡帠偼壜擻偱偡丅椺偊偽丄俙偐傜弌敪偡傞傕偺偩偗偵尷傟偽丄1/100偵側傞偺偼柧傜偐偱偡丅
偦傟偱傕偦偺寢壥丄椺偊扵嶕悢偑100壄暘偺1偵側偭偨偲偟偰傕從偗愇偵悈偱偡丅1020擭偱偡丅恾-1偵帵偟偨傛偆偵丄傢偞傢偞墦夞傝偡傞宱楬乮惵乯傕慡偰娷傑傟傞偐傜偱偡丅岎嵎揰100屄乮廲墶偵摴楬10杮掱搙乯側傫偰丄偪傚偭偲戝偒側挰側傜帩偭偰傞偼偢偱偡丅
偲偄偆栿偱僟僀僋僗僩儔偝傫偼丄嵟抁宱楬扵嶕傪岠棪壔偡傞僟僀僋僗僩儔朄傪峫偊傑偟偨丅僟僀僋僗僩儔朄偼婣擺朄偱徹柧偱偒傑偡偑丄扵嶕岠棪傪忋偘傞偨傔偺庤弴偑捛壛偝傟偰偄偰丄傢偐傝偵偔偄傕偺偵側偭偰偄傑偡丅偦偙偱丄僟僀僋僗僩儔朄傎偳岠棪偼椙偔側偄丄師偺婎杮僟僀僋僗僩儔乮壖徧偱偡乯傪峫偊傑偡丅
侾丏婎杮僟僀僋僗僩儔偺徹柧
嵟弶偵弌敪揰俙偲栚揑揰俛傪寛傔丄俙偐傜峴偗傞椬愙揰C1(1)丆C2(1)丆ゥCCa(1)傊偺宱楬挿傪寁嶼偟傑偡丅偦傟傜傪L1(1)丆L2(1)丆ゥCLa(1)偲偡傟偽丄偙傟偼俙偱暘婒偡傞摴楬偺摴楬挿偦偺傕偺偱偡丅傑偨擟堄偺Ci(1)偑丄俙偐傜偺嵟抁宱楬忋偵偁傞偺偼柧傜偐偱偡丅
丂宱楬挿Li(1)傪丄宱楬挿儕僗僩俴(1)亖{俴i(1)}偲偟偰婰榐偟傑偡丅
丂宱楬Pi(1)亖俙仺Ci(1)傪丄
宱楬儕僗僩俹(1)亖{Pi(1)}偲偟偰婰榐偟傑偡丅
師偵丄奺Ci(1)偐傜峴偗傞Cj(2)傪慡偰廤傔偰
C1(2)丆C2(2)丆ゥC
Cb(2)偲偟丄偦傟傜傊偺宱楬挿傪Lj(2)偲偟傑偡丅
Lj(2)偼丄Li(1)偵偦傟偧傟偺摴楬挿傪懌偡偩偗偱偡丅
宱楬Pj(2)亖俙仺Ci(1)仺Cj(2)傕嶌傝丄
偦傟偧傟儕僗僩偵壛偊傑偡丅
丂丂俴(2)亖{Li(1)丆Li(2)}
丂丂俹(2)亖{Pi(1)丆Pi(2)}
忋婰偺俴丆俹偼徣棯偟偰彂偄偰傑偡偑丄
杮摉偼俴(2)亖{Li(1)}伨{Li(2)}側偳偺堄枴偱偡丅
{Ci(2)}偵偼丄Ci(1)傊媡峴偡傞傕偺傕娷傑傟傑偡偟丄
媡峴偟側偔偰傕懠偺Cj(2)偵堦抳偡傞傕偺傕弌傞壜擻惈傕偁傝傑偡丅
偁傝傑偡偑丄偲傝偁偊偢婥偵偟傑偣傫丅
廳梫側偺偼{Ci(2)}偑丄2夞偺僗僥僢僾偱俙偐傜峴偗傞慡偰偺揰傪栐梾偟偰偄傞帠偱偡丅
俹(2)偵娷傑傟傞堦偮偺宱楬Pi(k)偵拲栚偟傑偡乮k亖1丆2乯丅
Pi(k)偼Ci(k)傊偺丄嵟抁宱楬偲偼尷傝傑偣傫丅壗屘側傜丄k夞埲壓偺僗僥僢僾m偱Ci(k)払偡傞Pj(m)偑偁偭偰丄
Li(k)傛傝Lj(m)偺曽偑抁偄偐傕偟傟側偄偐傜偱偡丅
傑偨(k亄1)夞埲忋偺僗僥僢僾n偱Ci(k)払偡傞丄傛傝抁偄Pj(n)偑丄偙偺愭弌傞偐傕偟傟側偄偐傜偱偡丅偟偐偟俴(k)偺嵟彫抣Lp(k)偵懳墳偡傞丄宱楬Pp(k)偲偦偺抂揰Cp(k)偵偮偄偰偼堘偄傑偡丅
Lp(k)偼k夞埲壓偺僗僥僢僾偱惗惉偝傟傞宱楬挿偺嵟彫側偺偱丄k夞埲壓偺僗僥僢僾偵尷傟偽丄宱楬Pp(k)偼丄抂揰Cp(k)傊偺嵟抁宱楬偱偡丅
偦傟傛傝彫偝側宱楬挿偑丄k夞埲壓偺僗僥僢僾偵偼側偄偐傜偱偡丅
偝傜偵丄(k亄1)夞埲忋偺僗僥僢僾偱Cp(k)偵払偡傞宱楬挿偼丄
慡偰Lp(k)傛傝戝偒偄帠偑尵偊傑偡丅
(k亄1)夞埲忋偺僗僥僢僾偱摓払偱偒傞揰偼慡偰丄k夞埲壓偱峴偗傞揰傪捠夁偟側偗傟偽側傜側偄偐傜偱偡丅
偙偙偱丄{Ci(k)}偑丄k夞偺僗僥僢僾偱俙偐傜峴偗傞慡偰偺揰傪栐梾偟偰偄傞帠偲丄Lp(k)偑俴(k)偺嵟彫抣偱偁傞帠偑岠偒傑偡丅
埲忋偺僗僥僢僾傪丄俛偵摓払偡傞傑偱孞傝曉偟傑偡丅
偄偮偐昁偢払偡傞偺偼柧傜偐偱偡丅
僗僥僢僾偺孞傝曉偟偺廔椆忦審偼丄
宱楬Pp(k)偺抂揰Cp(k)偑丄Cp(k)亖俛偲側傞帠偱偡丅
傕偆婣擺朄偵帩偪崬傓弨旛偼惍偄傑偟偨傛偹丠乮惍偄傑偟偨両丒丒丒壗偐朸撲妡偗寍恖傒偨偄偱偡偹^^乯丅側偺偱徹柧敳偒偱丄師偺婎杮掕棟乮偩偲巚偄傑偡乯傪偁偘傑偡丅
乵僟僀僋僗僩儔朄偺婎杮掕棟乶
丂俴(k)亖{Li(1)丆Li(2)丆ゥCLi(k)}偺嵟彫抣Lp(k)偵懳墳偡傞宱楬Pp(k)偼丄
偦偺抂揰Cp(k)傊偺嵟抁宱楬丅偨偩偟(k-1)埲壓偺僗僥僢僾偱嵟彫抣偲側偭偨傕偺偼丄嵟彫抣昡壙偐傜彍奜偡傞丅
乵徹柧乶
丂婣擺朄偵傛傞丅k亖1偺帪偼丄俹(1)亖{Pi(1)}偑慡偰嵟抁宱楬側偺偱丄婣擺朄偼惉棫偡傞丅
乵徹柧廔乶
偙偺婎杮掕棟偝偊傗偭偰偟傑偊偽丄屻偼扵嶕傪傕偭偲岠棪壔偡傞偩偗偱偡丅婎杮僟僀僋僗僩儔偺晄宱嵪側揰偼埲壓偱偡丅
丂丂(B-1)媡峴偡傞丅
丂丂(B-2)儖乕僾偡傞乮埲慜偺僗僥僢僾偱扵嶕偟偨揰偵栠傞乯丅
丂丂(B-3)婛偵嵟抁宱楬偑傢偐偭偨揰傕扵嶕丒昡壙偡傞丅
丂丂(B-4)傛傝抁偄宱楬偑偁傞偺偵丄偦偪傜偵扵嶕傪峣傜側偄丅
丂丂(B-5)堦夞偺僗僥僢僾偱丄晄梫偵墦偄揰傑偱扵嶕偡傞丅
(B-1)乣(B-5)傪夝徚偡傞偲丄師偺傢偐傝偵偔偄僟僀僋僗僩儔朄偵側傝傑偡丅
[侽]弶婜忬懺
丂丂(1)弌敪揰俙偲栚揑揰俛傪寛傔傞丅
丂丂(2)俙偐傜摓払偱偒傞椬愙揰俠1丆俠2丆ゥC俠s傊偺宱楬挿偲宱楬傪儕僗僩偡傞丅
丂丂(3)儕僗僩偺嵟彫抣偲側傞揰俠m傪尒弌偡丅宱楬俙仺俠m偑丄俠m傊偺嵟抁宱楬側偺偼柧傜偐丅
丂丂(4)俠m傪扵嶕揰偐傜彍奜偡傞丅
丂丂丂乮嵟抁宱楬偺傢偐偭偨揰偼扵嶕偟側偄乯
丂丂(5)俠m傪宱楬挿偲宱楬儕僗僩偐傜彍奜偟丄暿搑梡堄偟偨嵟抁宱楬儕僗僩偵丄俙仺俠m傪婰榐偡傞丅
丂丂丂乮嵟抁宱楬偺傢偐偭偨揰偼昡壙偟側偄乯
[侾]埲屻偺庤弴
丂丂(1)弌敪揰傪俠m偲偡傞丅
丂丂丂乮堦夞偺僗僥僢僾偱丄晄梫偵墦偄揰傑偱扵嶕偟側偄乯
丂丂(2)俠m偐傜摓払偱偒傞椬愙揰俢1丆俢2丆ゥC俢t傊偺丄俙偐傜偺宱楬挿偲丄俙偐傜偺宱楬傪儕僗僩偡傞丅
丂丂丂乮嵎暘傪懌偡偩偗乯
丂丂丂丂偨偩偟俢1丆俢2丆ゥC俢t偺拞偵丄宱楬俙仺ゥ▊bm偺揰偼娷傑側偄丅
丂丂丂乮媡峴偲儖乕僾嬛巭乯
丂丂(3)俢1丆俢2丆ゥC俢t偺拞偵丄俠i偲堦抳偡傞傕偺偑偁傟偽丄婛懚偺宱楬挿偲尰嵼偺宱楬挿傪斾妑偟丄抁偐偄傎偆偱丄俙偐傜偺宱楬挿儕僗僩偲俙偐傜偺宱楬儕僗僩傪抲偒姺偊傞丅偦偆偱側偄傕偺偼丄偨傫偵儕僗僩偵捛壛偡傞丅
丂丂丂乮傛傝抁偄宱楬傪桪愭乯
丂丂(4)俠1丆俠2丆ゥC俠s丆俢1丆俢2丆ゥC俢u偺宱楬挿偺拞偐傜丄嵟彫偺俢m傪慖傇丅
丂丂丂乮婎杮掕棟乯
丂丂(5)俢m傪扵嶕揰偐傜彍奜偡傞丅
丂丂丂乮嵟抁宱楬偺傢偐偭偨揰偼扵嶕偟側偄乯
丂丂(6)俢m傪宱楬挿偲宱楬儕僗僩偐傜彍奜偟丄嵟抁宱楬儕僗僩偵丄俙仺ゥ▊bm仺俢m傪婰榐偡傞丅
丂丂丂乮嵟抁宱楬偺傢偐偭偨揰偼昡壙偟側偄乯
[2]廔椆忦審
丂丂(1)俢m偑俛側傜廔椆偡傞乮栚揑揰偵払偟偨乯丅
丂丂(2)扵嶕揰偑側偄側傜廔椆偡傞乮俛偑嵟屻偵扵嶕偝傟偨乯丅
丂丂(3)(1)偱傕(2)偱傕側偄側傜丄俠m亖俢m偲偟偰[1]-(1)偵栠傞丅
丂婎杮僟僀僋僗僩儔偼丄堦夞偺扵嶕僗僥僢僾偛偲偵俛傊偺嵟抁宱楬偐斲偐傪敾掕偱偒傞揰傪彍偄偰丄偠偮偼懡暘栘慡扵嶕偲摨偠偱偡丅偟偐偟敾掕傾儖僑儕僘儉偑偁傞偺偱丄懡暘栘扵嵏偺嵟彫僗僥僢僾偱俛傊偺嵟抁宱楬偑摼傜傟丄偦偙偱寁嶼傪懪偪愗傟傑偡丅偙傟偑丄僟僀僋僗僩儔朄偑岠棪揑偱偁傞婎杮揑側棟桼偱偡丅
丂(B-1)丆(B-2)偺夝徚偼丄嵟抁宱楬扵嶕側傜偽昁偢枮偨偡傋偒惂栺側偺偱丄偙傟傜偱杮幙揑偵懍偔側傞栿偱偼偁傝傑偣傫偑丄懡彮懍偔側傞偺偼妋幚偱偡丅
丂(B-3)偺夝徚偼丄僟僀僋僗僩儔朄傪杮幙揑偵懍偔偟傑偡丅(B-3)傪夝徚偡傟偽丄堦夞偺扵嶕僗僥僢僾偛偲偵扵嶕揰偑堦屄偯偮尭偭偰偄偔偺偱丄昁梫扵嶕検偺忋尷偑1/n偯偮暋棙偱尭傞帠懺傪彽偒傑偡丅偙偙偱n偼丄奺揰偺暘婒悢偺暯嬒掱搙偺惍悢偱偡丅懡暘栘扵嶕偱扵嶕悢偑丄nm乮m丗扵嶕揰悢乯偺暋棙偱憹偊傞偺偲媡偺忬嫷偱偡丅僟僀僋僗僩儔朄偼丄屻敿偵峴偔傎偳僗僺乕僪傾僢僾偟傑偡丅
丂(B-4)丆(B-5)偺夝徚傕丅僙僢僩偱杮幙揑側壛懍偱偡丅傾儖僑儕僘儉偲偟偰偼丄[0]-(3)傑偨偼[2]-(3)偐傜[1]-(1)傊偺堏峴偲丄[1]-(3)偺儕僗僩峏怴偲偟偰幚憰偝傟傑偡丅
丂[1]偱慖戰偝傟偨俢m揰傊偺宱楬偼忢偵丄尰僗僥僢僾偱偺乽嵟嵟抁宱楬乿偱偡丅偦偙偵師偺扵嶕僗僥僢僾傪峣傝傑偡丅偦偆偡傞偲僟僀僋僗僩儔朄偱偼丄k夞栚偺僗僥僢僾偱丄k夞偺僗僥僢僾偱摓払偱偒傞揰傪乽慡偰栐梾偼偟側偄乿帠偵側傝傑偡丅偨偩偟丄k夞埲壓偺僗僥僢僾偱偼丄昁偢栐梾偝傟偰偄傞僗僥僢僾偑懚嵼偟傑偡丅椺偊偽k亖1偼丄柧傜偐偵栐梾偱偡丅
丂尰僗僥僢僾偱偺乽嵟嵟抁宱楬乿傪慖傇偺偱丄乽嵟嵟抁宱楬乿偼丄栐梾偝傟偨僗僥僢僾偺揰偺懁偐傜寛傑偭偰偄偒傑偡丅寢壥偲偟偰丄俙揰偐傜偺嬤偝偺弴偵嵟抁宱楬偑寛傑傝傑偡丅偙傟偵傛偭偰晄梫偵墦偄揰傑偱扵嶕偡傞帠偑杊偑傟傑偡丅俛偑俙偐傜10斣栚偵嬤偄揰側傜丄10僗僥僢僾偱摓払偱偒傞栿偱偡丅
丂偙偺傛偆側僟僀僋僗僩儔朄偺寁嶼検偼m2偵斾椺偟傑偡乮徹柧偱偒傑偣傫乯丅偱偡偑丄屄恖揑偵斾妑偱偒傞傾儖僑儕僘儉偲偟偰偼丄m尦楢棫堦師曽掱幃傪夝偔丄僈僂僗偺徚嫀朄偑偁傝傑偡丅偙傟偺寁嶼検偼丄m3偵斾椺偱偡丅尰峴偺昗弨巗斕PC偺CPU丄1GHz亊quad Core側傜丄m亖10000偱偁偭偰傕1000杮偺嵟抁宱楬寛掕偵丄挿偔偰悢昩偲梊憐偱偒傑偡丅
丂僟僀僋僗僩儔朄偼丄乽尵傢傟偰傒傟偽摉偨傝慜乿偺帠傪傗偭偰偄傑偡丅偟偐偟偦傟傪丄偙偙傑偱惍棟偟偰掕幃壔偟偨僟僀僋僗僩儔偝傫偼丄傗偭傁傝偡偛偄偲巚偄傑偡丅
俀丏桳尷梫慺朄
帺暘偺杮摉偺愱栧偼丄峔憿壆偱嫶椑壆偱偡丅偦傟偑偳偆偟偰僟僀僋僗僩儔朄側傫偐傪帩偪弌偟偨偐偲尵偆偲丄媣偟傇傝偵桳尷梫慺朄夝愅傪棅傑傟偨偐傜偱偡丅巜掕偝傟偨夝愅僜僼僩偼撻愼傒怺偄傕偺偱丄嵟弶偼偦傫側偵婥偵偟偰傑偣傫偱偟偨丅偲偙傠偑偦偺夝愅僜僼僩傪媣偟傇傝偵巊梡偟偨偲偙傠丄嫲傠偟偔晄曋側偺偵婥偯偒傑偟偨乮愗傟偐偗傑偟偨乯丅愄偼晄曋偝偵丄婥偯偄偰偄側偐偭偨偺偱偡丅偲偄偆栿偱丄桳尷梫慺朄傪奣愢偝偣偰捀偒傑偡乮仼慡偔棟桼偵側偭偰側偄^^;乯丅
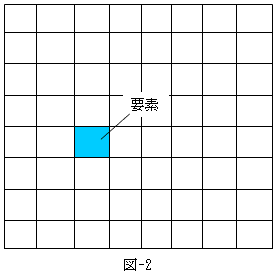 桳尷梫慺朄偑揔梡偝傟傞揟宆揑側忬嫷偼丄椺偊偽惓曽宍偺揝偺夠偑偁偭偰丄偦傟偑帺廳偱偳偺傛偆偵曄宍偡傞偺偐傪寁嶼偟偨偄応崌偱偡丅恾-2偺岄斦偺栚偱嬫愗傜傟偨惓曽宍偑丄崱夞偺揝偺夠偱偡丅岄斦偺栚偺帠傪儊僢僔儏偲尵偄丄栚偺堦偮堦偮傪梫慺偲尵偄傑偡丅
桳尷梫慺朄偑揔梡偝傟傞揟宆揑側忬嫷偼丄椺偊偽惓曽宍偺揝偺夠偑偁偭偰丄偦傟偑帺廳偱偳偺傛偆偵曄宍偡傞偺偐傪寁嶼偟偨偄応崌偱偡丅恾-2偺岄斦偺栚偱嬫愗傜傟偨惓曽宍偑丄崱夞偺揝偺夠偱偡丅岄斦偺栚偺帠傪儊僢僔儏偲尵偄丄栚偺堦偮堦偮傪梫慺偲尵偄傑偡丅
桳尷梫慺朄偺慜採偼丄偠偮偼堦斒揑側暔棟揑壖掕偲悢妛揑尨棟偵偁傝傑偡丅偄傑惓曽宍偺曄宍忬嫷傪抦傝偨偄偺偱丄恾-2偵x-y嵗昗傪擖傟丄惓曽宍偺奺揰偺x曽岦丆y曽岦偺曄埵dx丆dy偑丄(x丆y)偺娭悢偲偟偰傢偐傟偽OK偱偡丅
丂丂丂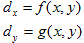
偮傑傝d亖(dx丆dy)偼丄曄宍慜偲曄宍屻偺偁傞揰偺嵗昗偺嵎d亖(x亄dx丆y亄dy)亅(x丆y)偱偡丅
桳尷梫慺朄偺嵟弶偺慜採偼丄師偺宱尡帠幚偲悢妛揑尨棟偱偡丅
丂丂(1)暔棟検偼丄傒側旝暘壜擻偱偁傞丅
丂丂(2)旝暘壜擻側傜丄嬊強揑偵慄宍嬤帡乮斾椺攝暘乯壜擻丅偙傟偼旝暘偺堄枴偦偺傕偺丅
(1)傛傝(dx丆dy)偼丄旝暘壜擻偱偡丅偦偟偰乽嬊強揑偵乿側偺偱丄恾-2偺梫慺偑廫暘彫偝偄偲偟偰丄(dx丆dy)傪梫慺忋偱峫偊傞偲寢榑偲偟偰丄梫慺偺曄宍偵懳偟偰師偺榗傒暘夝偑摼傜傟傑偡丅
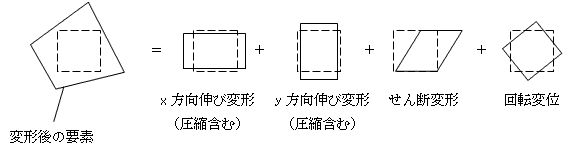
嬊強揑偵偼梫慺偺曄宍偼丄x丆y曽岦偺怢傃偵懳墳偡傞曄埵丄偣傫抐曄宍偵懳墳偡傞曄埵丄夞揮偵懳墳偡傞曄埵偺丄偨傫側傞懌偟嶼偵側傝傑偡丅懌偟嶼側傞偺偼丄(dx丆dy)偑旝暘壜擻偱嬊強揑偵慄宍嬤帡壜擻偩偐傜偱偡丅
嵽椏偼曄宍偵懳偟偰掞峈偟傑偡丅椺偊偽x曽岦偵怢傃偨傜丄偁傞椡偱x曽岦偵弅傕偆偲偟傑偡乮僶僱傪憐憸偟偰壓偝偄乯丅捠忢偺桳尷梫慺朄偱偼丄偙偙偱2偮栚偺暔棟揑壖掕偺搊応偱偡丅
丂丂(3)曄宍偼丄旝彫偱偁傞丅
偙傟偼戝掞惉傝棫偪傑偡丅椺偊偽壗10枩t偲偄偆僞儞僇乕偱傕丄帺廳偱旝彫偵偟偐曄宍偣偢帺棫偱偒傞偺偱丄寶憿拞偵姡僪僢僋偵抲偄偰偍偗傑偡丅
曄宍偵墳摎偡傞掞峈傕暔棟検偱偡丅(1)傛傝旝暘偱偒傑偡丅偟偐傕曄宍偼旝彫偱偡丅(2)傪尵偄姺偊傞偲乽旝暘壜擻側傜丄旝彫擖椡偵懳偡傞墳摎偼丄擖椡偵斾椺偡傞乿偱偡丅偮傑傝榗傒暘夝偺奺曄宍儌乕僪偵懳偟偰丄杮摉偵僶僱傪憐掕偱偒傞偲偄偆帠偱偡丅榗傒暘夝偺曄宍儌乕僪偺偆偪丄梫慺傪杮摉偵曄宍偝偣偰偄傞偺偼丄嵟弶偺3偮偱偡丅偦傟偱梫慺偵偼丄師偺傛偆側僶僱偑撪憼偝傟偰偄傞偲峫偊傑偡丅
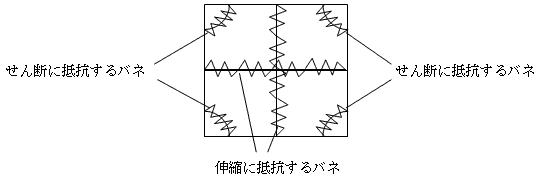
榗傒暘夝偺恾偐傜傢偐傞傛偆偵丄偙傟傜偺僶僱偺怢傃弅傒偼丄梫慺偺巐偮妏偺揰偺曄埵偑巟攝偟傑偡丅僶僱掕悢偼丄揝側傜揝偺曄宍偵傆偝傢偟偄傛偆偵嵽幙偵崌傢偣偰挷惍偟丄幚嵺偺枹抦悢偼丄梫慺偺巐偮妏偺曄埵偲偄偆棧嶶壔検偱偡丅
埲忋偺庤弴偱丄恾-2偺岄斦偺栚偺栚傪慡偰僶僱儌僨儖偱偍偒偐偊丄暔懱傊偺奜椡傪梌偊傞偲丄僶僱傪弅傑偣傞乮怢偽偡乯巐偮妏偺曄埵偵娭偡傞楢棫堦師曽掱幃偑摼傜傟傑偡丅偦傟傪夝偄偰慡偰偺梫慺偺巐偮妏曄埵傪摼偨傜丄嵞傃梫慺偑彫偝偄帠傪棙梡偟偰乮(1)丆(2)傪棙梡偟偰乯丄巐偮妏曄埵偺抣偐傜梫慺撪晹偺揰偺曄埵傪丄慄宍嬤帡偱媮傔傑偡丅偙傟偱廔椆偱偡丅
桳尷梫慺朄偼(1)丆(2)丆(3)偲偄偆堦斒揑尨棟偵婎偯偄偰偄傞偺偱丄傎偲傫偳偺応崌偱尰徾偵憡摉偡傞僶僱儌僨儖偑懚嵼偟丄傎偲傫偳偁傜備傞暘栰偵揔梡壜擻側嬤帡寁嶼朄偱偡乮塅拡榑偵傕乯丅偲偼尵偊乽儊僢僔儏傪愗傜側偒傖巒傑傜側偄乿丒丒丒帠偼丄傢偐偭偰捀偗傞偲巚偄傑偡丅
暔懱側偳偺宍忬乮夝愅椞堟乯偑扨弮側傜丄恾-2偺傛偆側岄斦偺栚儊僢僔儏偱嵪傒傑偡偑丄宍忬偑暋嶨偩偲偦偆偼偄偒傑偣傫丅偠偭偝偄桳尷梫慺朄偱堦斣庤偑偐偐傞偺偼丄幚偼偙偺乽儊僢僔儏愗傝嶌嬈乿側偺偱偡丅
俁丏椞堟擣幆
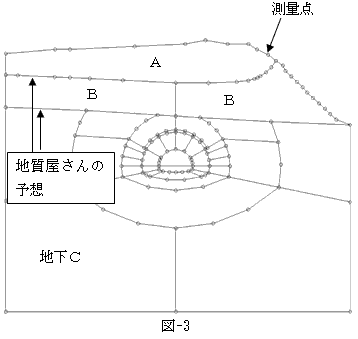 恾-3偼丄偲偁傞嶳偺抐柺偱偡丅嶳偺宍偼儔僕僐儞婡偵傛傞峲嬻應検偺寢壥偲巚傢傟傑偡丅恾拞偺俙丆俛丆俠偺椞堟偱偼丄搚傗娾偺屌偝偑堘偄傑偡丅俙丆俛丆俠偺嫬偺儔僀儞偼丄儃乕儕儞僌挷嵏傪傕偲偵丄抧幙壆偝傫偑梊憐偟偨傕偺偱偡乮屌偝傕乯丅恀傫拞曈傝偵偁傞敿墌忬偺椞堟偼丄偙偺嶳偵孈嶍梊掕偺僩儞僱儖斖埻偱偡丅
恾-3偼丄偲偁傞嶳偺抐柺偱偡丅嶳偺宍偼儔僕僐儞婡偵傛傞峲嬻應検偺寢壥偲巚傢傟傑偡丅恾拞偺俙丆俛丆俠偺椞堟偱偼丄搚傗娾偺屌偝偑堘偄傑偡丅俙丆俛丆俠偺嫬偺儔僀儞偼丄儃乕儕儞僌挷嵏傪傕偲偵丄抧幙壆偝傫偑梊憐偟偨傕偺偱偡乮屌偝傕乯丅恀傫拞曈傝偵偁傞敿墌忬偺椞堟偼丄偙偺嶳偵孈嶍梊掕偺僩儞僱儖斖埻偱偡丅
僩儞僱儖傪孈嶍偟偨傜丄嶳偺墳椡忬懺乮撪晹偺椡乯偑偳偆側傞偐丠傪妋擣偡傞偨傔偵丄桳尷梫慺朄傪峴偄傑偡丅偮傑傝棊斦側偳偑怱攝側偺偱偡丅墳椡忬懺偼曄宍検偐傜僶僱儌僨儖偺僶僱偺怢傃弅傒傪寁嶼偟丄怢傃弅傒検偵僶僱掕悢傪偐偗傟偽摼傜傟傞偺偱丄寢嬊傗傞帠偼偝偭偒偲偄偭偟傚偱偡丅
偨偩偟崱搙偼丄夝愅椞堟偺宍偑傗傗暋嶨側帠丄嵽椏掕悢乮僶僱掕悢乯偑椞堟偛偲偵堎側傞帠偐傜丄嵟掅尷俙丆俛丆俠偺椞堟傪丄夝愅僜僼僩偵擖椡偡傞昁梫偑偁傝傑偡丅僩儞僱儖斖埻偑偨偔偝傫偺椞堟偵暘偐傟偰偄傞偺偼丄抧斦夵椙側偳偺岺朄傪暪梡偟丄抧嶳偺惈幙乮僶僱掕悢乯偑曄傢偭偰偔傞偐傜偱丄偙傟傜傕擖椡偡傞昁梫偑偁傝傑偡丅偦偺懠偺儔僀儞偼丄鉟楉側儊僢僔儏傪摼傞偨傔偺曗彆儔僀儞偱偡偑丄偦傟傜偵傛偭偰偝傜偵椞堟偑憹偊傑偡丅
 夝愅僜僼僩偵椞堟傪擣幆偝偣偨屻偼丄椞堟偛偲偵丄捠忢偼Advancing Front朄傪梡偄偰敿帺摦偺儊僢僔儏惗惉傪峴偄傑偡丅摼傜傟偨儊僢僔儏偼丄恾-4偱偡偑丄偙偙傑偱棃傞偺偑戝曄偱偟偨丅
夝愅僜僼僩偵椞堟傪擣幆偝偣偨屻偼丄椞堟偛偲偵丄捠忢偼Advancing Front朄傪梡偄偰敿帺摦偺儊僢僔儏惗惉傪峴偄傑偡丅摼傜傟偨儊僢僔儏偼丄恾-4偱偡偑丄偙偙傑偱棃傞偺偑戝曄偱偟偨丅
恾-3偺娵偼婔壗妛揑側揰傪昞偟丄恾-3偺宍忬偼揰傪偮側偖儔僀儞偺廤愊偱偡丅椞堟傪掕媊偡傞偲偼丄偦偺儔僀儞偺廤愊偵埵憡忣曬乮揰偺偮側偑傝曽乯傪梌偊傞偲偄偆帠偱偡丅婎杮偼丄椞堟嫬奅偺慡偰偺揰傪丄嫬奅偵増偆弴斣偱庤擖椡偱偡丅偦偆偡傞偲椺偊偽丄塃懁偺俛偺椞堟偺擣幆側偳偼丄偗偭偙偆側柺搢抧摴側嶌嬈偵側傝傑偡丅偟偐傕巊梡偟偨撻愼傒偺僜僼僩偼丄揰偺擣幆偑娒偄偲偄偆寚揰傪帩偪丄椞堟偵栚偵尒偊側偄寗娫偑偱偒傞帠傕丄偟偽偟偽偱偟偨丅偦偺忋丄撻愼傒偺偙偺屆偄僜僼僩偼丄婛偵Windows偺屆揟昗弨偲壔偟偰偄傞乽Undo婡擻乿傪帩偨側偄巒枛偱偡丅偮傑傝寗娫傪側偔偡傞嶌嬈偼丄慡偰乽嵟弶偐傜傗傝捈偟乿側偺偱偡丅
愄偺椞堟擣幆嶌嬈偼丄巻偺恾柺忋偱僨僔僞僀僓乕偲偄偆婡夿傪梡偄丄拵娽嬀偺僞乕僎僢僩撪偵堦揰堦揰傪懆偊偰埵抲傪婰榐偟丄埵抲偺悢抣僨乕僞傪PC偵怘傢偣傞偲偄偆丄崱巚偊偽丄偲偰傕恖娫偑傗傞傛偆側嶌嬈偱偼偁傝傑偣傫偱偟偨丅偦傟傪夋柺忋偺僋儕僢僋堦敪偱張棟偡傞丄偙偺僜僼僩偑尰傟偨帪偵偼夋婜揑偱丄晄曋偝偵婥偯偄偰偄側偐偭偨偺偱偡丅
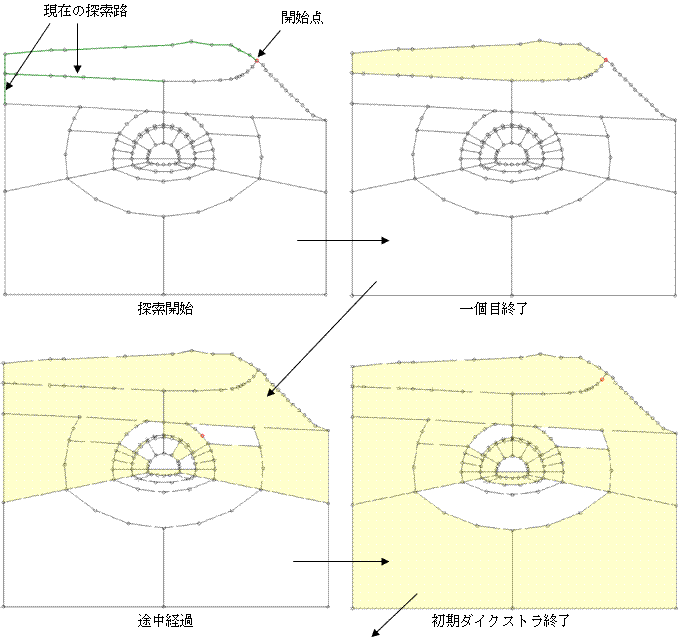
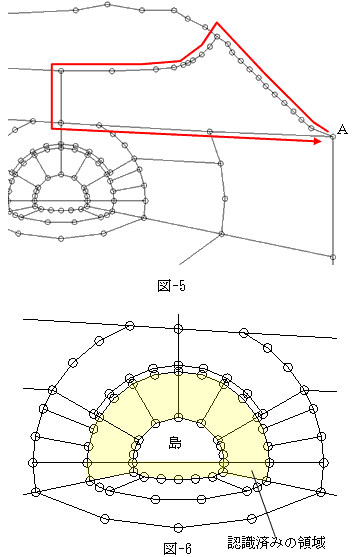 偱丄椞堟偺帺摦擣幆偼偱偒側偄偐丠丄偲峫偊傑偟偨丅僟僀僋僗僩儔朄偺弌斣偱偡丅恾-5偵帵偡傛偆偵丄揰俙偐傜弌敪偟偰丄揰俙偵栠傞傛偆側嵟抁宱楬傪扵偣偽偄偄偠傖側偄偐丠丄偲偄偆敪憐偱偡丅偦傟偼僟僀僋僗僩儔朄偱丄弌敪揰偲栚揑揰傪堦抳偝偣傟偽壜擻偱偡丅
偱丄椞堟偺帺摦擣幆偼偱偒側偄偐丠丄偲峫偊傑偟偨丅僟僀僋僗僩儔朄偺弌斣偱偡丅恾-5偵帵偡傛偆偵丄揰俙偐傜弌敪偟偰丄揰俙偵栠傞傛偆側嵟抁宱楬傪扵偣偽偄偄偠傖側偄偐丠丄偲偄偆敪憐偱偡丅偦傟偼僟僀僋僗僩儔朄偱丄弌敪揰偲栚揑揰傪堦抳偝偣傟偽壜擻偱偡丅
偨偩偙偺曽朄偵偼丄2偮偺寚揰偑偁傞偺偼丄嵟弶偐傜傢偐偭偰偄傑偟偨丅堦偮偼搰偑巆傞帠偱偡丅
奺椞堟偺暘婒揰乮嶰嵆楬埲忋偵側偭偰偄傞岎嵎揰乯偐傜弌敪揰偵栠傞扵嶕傪弴師峴偆偲偡傞偲丄奜廃偑抁偄椞堟偐傜弴斣偵擣幆偝傟傑偡丅傑偨偁傞暘婒揰偺暘婒曈偑懏偡傞椞堟偑妋掕偟偨側傜丄偦偺揰偐傜弌敪偡傞扵嶕偵偍偄偰偼丄妋掕曈偼擇搙偲扵嶕偡傞傋偒偱偁傝傑偣傫丅摨偠椞堟偑擇廳偵惗偠傞偐傜偱偡丅
偦偆偡傞偲椞堟偺戝偒偝偵傛偭偰偼丄偦偺廃埻偺椞堟偑慡偰愭偵擣幆偝傟丄恾-6偺乽搰乿偲恾帵偟偨椞堟偵偮偄偰偼丄扵嶕偑峴傢傟側偄帠偵側傝傑偡丅
偙傟傊偺夝寛嶔偼丄偨傫偵柍帇偡傟偽OK偩偲婥偯偒傑偟偨丅弶婜偺忬懺偱傗傟傞偲偙傠傑偱僟僀僋僗僩儔傪傗偭偨屻偱丄2偮偺椞堟偵懏偡傞儔僀儞偲揰傪慡偰嶍彍偡傟偽丄屒棫偟偨搰偩偗偑巆傝傑偡丅屒棫偟偨搰偱偼扵嶕晄梫側偺偱丄偦傟傜偺擣幆偼堦弖偱偡丅
傕偆堦偮偺寚揰偼丄暋崌椞堟偑弌棃偆傞帠偱偡丅弌敪揰偵栠傞嵟抁宱楬偑丄昁偢偟傕扨堦椞堟偵懳墳偟側偄帠偱偡丅恾-7偼偦偺椺偱偡丅愒偺儖乕僩偼惵偺儖乕僩傛傝抁偄丄偲偄偆寢壥偵側傝傑偡丅偦傟偱弶夞偼愒偺儖乕僩偑擣幆偝傟丄暋崌椞堟偵側傝傑偡丅
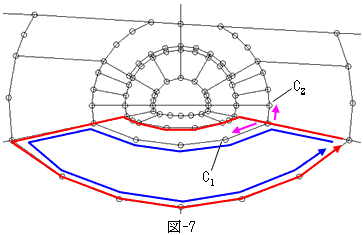 壜擻惈偲偟偰偼丄愒偲惵偑惓妋偵摍挿偲偄偆応崌傕偁傝摼傑偡丅偦偺応崌偼丄僟僀僋僗僩儔朄偺嵟彫抣敾掕偱丄嬼慠偵愒偑慖偽傟偨栿偱偡丅
壜擻惈偲偟偰偼丄愒偲惵偑惓妋偵摍挿偲偄偆応崌傕偁傝摼傑偡丅偦偺応崌偼丄僟僀僋僗僩儔朄偺嵟彫抣敾掕偱丄嬼慠偵愒偑慖偽傟偨栿偱偡丅
暋崌椞堟偵側偭偨傜丄屻弎偺孞傝曉偟偵帩偪崬傫偱張棟偱偒傞偺偱丄傑偢偼柍帇偟偰OK偲傢偐傝傑偟偨丅偨偩偟暋崌椞堟敾掕偼昁梫偱偡丅偦傟偵偼惗惉偝傟偨埵憡忣曬傪棙梡偱偒傑偡丅
扨堦偱傕暋崌偱傕丄偲偵偐偔椞堟偲偟偰擣幆偝傟偨傜丄椞堟嫬奅忋偺揰偺弴彉廤崌偑摼傜傟傑偡乮塃廃傝偐嵍廃傝乯丅偦偺拞偐傜嶰嵆楬埲忋偵側偭偰偄傞揰傪慖傃丄暘婒偑嫬奅忋偵側偄帠傪妋擣偟偰丄暘婒偵増偭偰1儔僀儞恑傒傑偡丅恾-7偺C1偲C2偱偡丅慡偰偺嶰嵆楬埲忋偺岎嵎揰偱丄C1偺傛偆側撪晹揰偑側偗傟偽丄扨堦椞堟偱偡丅
揰偺椞堟撪晹乛奜晹乛嫬奅忋偺敾掕偵傕丄埵憡忣曬傪棙梡偱偒傑偡丅揰偲嫬奅揰傪寢傇捈慄偺妏搙傪丄弴彉廤崌偵廬偭偰塃夞傝偐嵍夞傝偐偱弴師寁嶼偟丄妏搙憹暘傪愊嶼偡傟偽寢壥偼丄奜晹丗0丆撪晹丗亇2兾丆嫬奅丗亇兾偱偡丅偙傟偼丄弴彉廤崌偵廬偭偰帺暘偑嫬奅揰傪栚帇偟偰偄偭偨応崌丄帺暘偺庱偑偳偺傛偆偵夞傞偐憐憸偡傟偽丄偡偖傢偐傝傑偡丅0丆兾丆2兾偺暘棧偼旕忢偵柧妋側偺偱丄僐儞僺儏乕僞乕偺悢抣岆嵎傪峫椂偟偰傕丄傑偢娫堘偆帠偼偁傝傑偣傫丅
埲忋偺張棟傪姰椆偡傟偽丄巆傞偺偼屒棫偟偨扨堦搰偐暋崌搰偱偡丅暋崌搰偑偁傟偽扨堦搰偼慡偰柍帇偟丄暋崌搰偺撪晹扵嶕傪峴偄傑偡丅
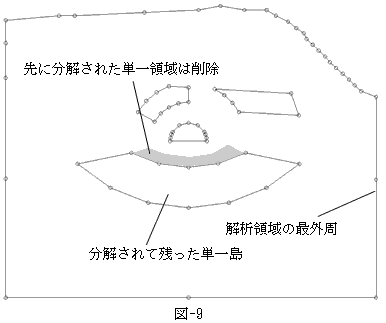
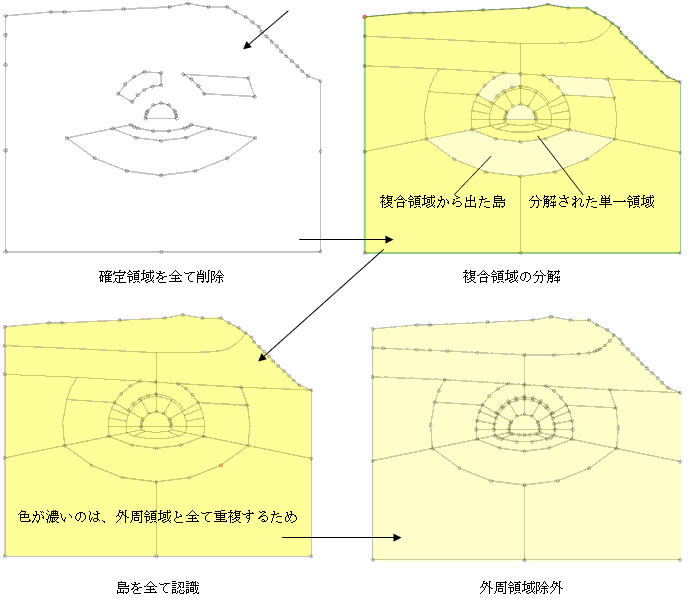
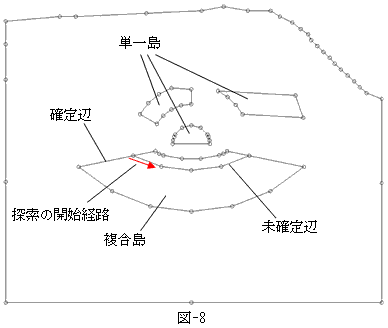 暋崌搰偺奜廃偼丄偦偺奜懁偺乮徚偟偰偟傑偭偨乯椞堟偺妋掕偵敽偭偰丄妋掕曈偵側偭偰偄傑偡丅堦曽撪晹偺曈偼丄傑傢傝偺椞堟偑妋掕偟偰偄側偄偺偱丄慡偰枹妋掕曈偱偡丅傛偭偰崱傑偱偺傾儖僑儕僘儉傪偨傫偵孞傝曉偟揔梡偡傞偩偗偱丄恾-8偺愒偱帵偟偨傛偆側扵嶕偑帺摦偱巒傑傝丄暋崌椞堟偼扨堦椞堟偵偄偮偐偼暘夝偝傟偰嵟屻偵巆傞偺偼丄傕偲傕偲偺屒棫搰偲丄暋崌搰偐傜敪惗偟偨屒棫搰偺傒偱偡乮恾-9乯丅
暋崌搰偺奜廃偼丄偦偺奜懁偺乮徚偟偰偟傑偭偨乯椞堟偺妋掕偵敽偭偰丄妋掕曈偵側偭偰偄傑偡丅堦曽撪晹偺曈偼丄傑傢傝偺椞堟偑妋掕偟偰偄側偄偺偱丄慡偰枹妋掕曈偱偡丅傛偭偰崱傑偱偺傾儖僑儕僘儉傪偨傫偵孞傝曉偟揔梡偡傞偩偗偱丄恾-8偺愒偱帵偟偨傛偆側扵嶕偑帺摦偱巒傑傝丄暋崌椞堟偼扨堦椞堟偵偄偮偐偼暘夝偝傟偰嵟屻偵巆傞偺偼丄傕偲傕偲偺屒棫搰偲丄暋崌搰偐傜敪惗偟偨屒棫搰偺傒偱偡乮恾-9乯丅
恾-9偺忬懺傑偱棃偨傜丄屻偼屒棫搰傪慡偰擣幆偝偣偰廔椆丒丒丒偲巚偭偨偺偱偡偑丄嵟屻偺栤戣偑偁傝傑偟偨丅
 搰偺掕媊偼偙偆偱偡丅
搰偺掕媊偼偙偆偱偡丅
丂丂乽嫬奅忋偺慡偰偺揰偑丄擇暘栘偱偁傞帠乿丅
偙傟偼慡偰偺揰偑岎嵎揰偱側偄帠傪尵偭偰偄傑偡偑丄偙偺忦審偵丄夝愅椞堟偺嵟奜廃偑奩摉偟偰偟傑偄傑偡丅
夝愅椞堟偺嵟奜廃傪椞堟偲偟偰擣幆偝偣傞偲丄撪晹偺慡偰偺扨堦椞堟偲廳暋偑惗偠偰丄椞堟偛偲偵儊僢僔儏傪愗傞偲偄偆嶌嬈偑偱偒側偔側傝傑偡丅
尰嵼偼嶍彍偟偨儔僀儞偲揰傪暅媽偟偨屻丄慡偰偺揰傪娷傓椞堟偼晄壜丄偲偄偆曽朄偱懳張偟偰偄傑偡偑丄傕偭偲姰慡側曽朄偑昁梫偩偲丄偦偺屻巚偄傑偟偨丅
偲偄偆偺偼丄偙偙傑偱偺嶌嬈傪幚峴偡傞僾儘僌儔儉偼丄婛偵Application偺懺傪惉偟偰偄傑偡丅偙偺傑偱偱廔傢傜偣傞偺偼栜懱側偄偺偱丄椞堟偛偲偺姰慡帺摦儊僢僔儏傑偱傗傠偆偲巚偭偰偄傑偡丅偦偺壙抣偼丄恾-3偵傛偆偵傗偨傜偲椞堟傪憹傗偝偢偵丄昁梫嵟彫尷偺撪晹椞堟偩偗偱夝愅椞堟傪掕媊偟丄壗偺庤傕偐偗偢偵帺摦儊僢僔儏偱偒傞帠偱偡丅
恾-3偺傛偆側乽恾柺乿偼丄偄偔傜惢恾僜僼僩偑敪払偟偨偲偼尵偊丄寢嬊偼庤偱昤偒傑偡丅傑偨椞堟擖椡屻偵恾-4偺儊僢僔儏傪敪惗偝偣傞偨傔丄椞堟嫬奅偺暘妱悢傪庤摦偱挷惍偡傞偲偄偆丄傕偆堦嶳嶌嬈傕偁傝傑偟偨丅
姰慡帺摦偺椞堟擣幆亅儊僢僔儏惗惉偑憳嬾偡傞揟宆揑忬嫷偼丄恾-10偺傛偆側傕偺偩偲巚偄傑偡丅偮傑傝屒棫椞堟偑婎杮偱偡丅偲偄偆帠偼丄崱傑偱奜廃偟偐帩偨側偄扨堦椞堟偱峫偊偰棃傑偟偨偑丄撪廃傪帩偮椞堟傊偺懳張偑惀旕昁梫偱偡丅屒棫偑婎杮偩偐傜偱偡丅偦傟偵偼丄偦傟偧傟傪奜廃偟偐帩偨側偄扨堦椞堟偲偟偰擣幆偝偣丄廳暋傪婲偙偝偣側偄偨傔偵椞堟偺曪娷娭學傪惍棟偟偰丄廳暋傪帩偮椞堟偵撪廃傪捛壛偡傞昁梫偑偁傝傑偡丅偮傑傝椞堟偺曪娷弴彉偺奒憌壔偱偡丅埵憡忣曬傪棙梡偟偰丄椞堟娫偺娷傓乛娷傑側偄娭學偼偡偖敾掕偱偒傑偡偑丄扨弮偵傗傞偲懡暘栘傪巊偭偨宱楬扵嶕偺傛偆側栚偵崌偆傛偆側婥偑偟偰丄尰嵼偼曽恓傪専摙拞偱偡丅
偲偼尵偊丄偙偙傑偱偺寢壥偵偼偄偪偍偆枮懌偟偰偄傑偡丅嵟屻偵椞堟擣幆夁掱偺恾傪偁偘傑偡丅
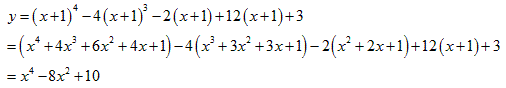

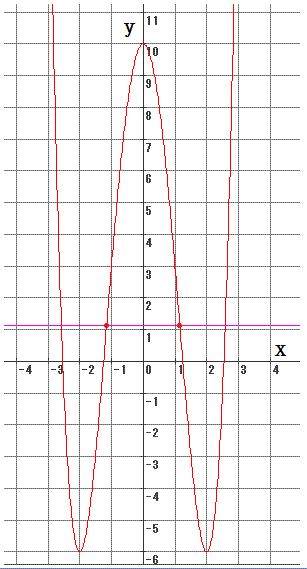
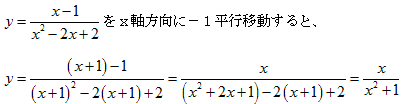
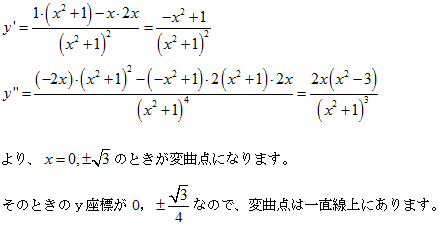

 丂丂丂(1)
丂丂丂(1)
 丂丂丂(2)
丂丂丂(2) 丂丂丂(3)
丂丂丂(3) 丂丂丂(4)
丂丂丂(4) 丂丂丂(5)
丂丂丂(5)
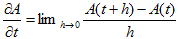
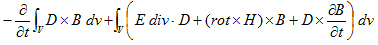 丂丂丂(6)
丂丂丂(6)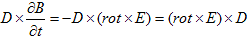
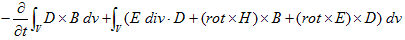 丂丂丂(7)
丂丂丂(7)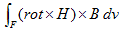 丂丂丂(8)
丂丂丂(8)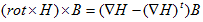 丂丂丂(9)
丂丂丂(9)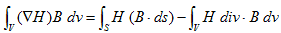 丂丂丂(10)
丂丂丂(10)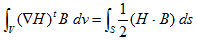 丂丂丂(11)
丂丂丂(11)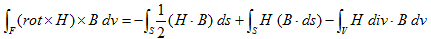 丂丂丂(12)
丂丂丂(12)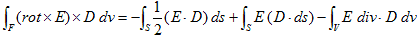 丂丂丂(13)
丂丂丂(13)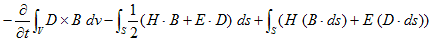 丂丂丂(14)
丂丂丂(14)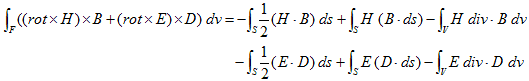
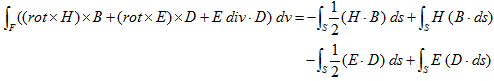 丂丂丂(15)
丂丂丂(15)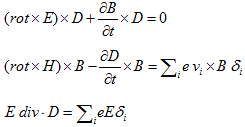
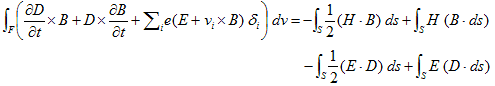
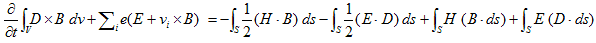 丂丂丂(16)
丂丂丂(16)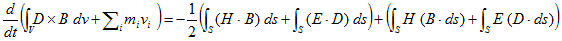 丂丂丂(17)
丂丂丂(17)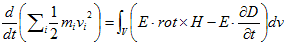 丂丂丂(1)
丂丂丂(1)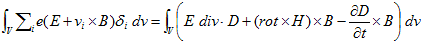 丂丂丂2.(4)
丂丂丂2.(4)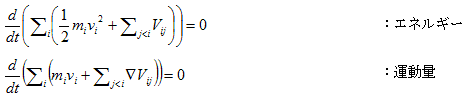
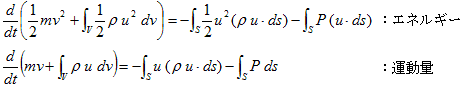
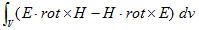 丂丂丂(2)
丂丂丂(2)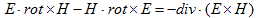 丂丂丂(3)
丂丂丂(3)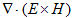 丂丂丂(4)
丂丂丂(4)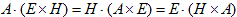 丂丂丂(5)
丂丂丂(5)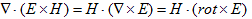 丂丂丂(6)
丂丂丂(6)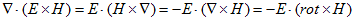 丂丂丂(7)
丂丂丂(7)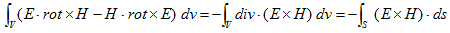
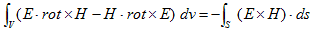 丂丂丂(8)
丂丂丂(8)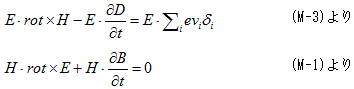
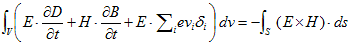 丂丂丂(9)
丂丂丂(9)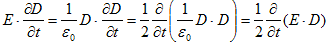 丂丂丂(10)
丂丂丂(10)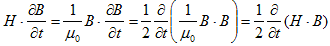 丂丂丂(11)
丂丂丂(11)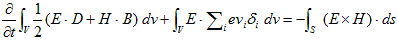 丂丂丂(12)
丂丂丂(12)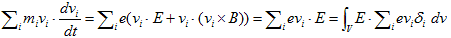
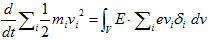 丂丂丂(13)
丂丂丂(13)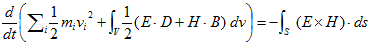 丂丂丂(14)
丂丂丂(14)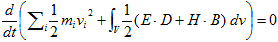 丂丂丂(15)
丂丂丂(15)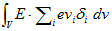 丂丂丂(16)
丂丂丂(16)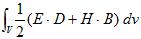 丂丂丂(17)
丂丂丂(17)
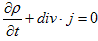 丂丂丂(1)
丂丂丂(1)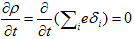
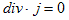 丂丂丂(2)
丂丂丂(2)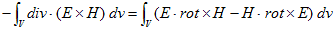 丂丂丂(3)
丂丂丂(3)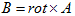 丂丂丂(4)
丂丂丂(4)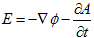 丂丂丂(5)
丂丂丂(5)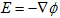 丂丂丂(6)
丂丂丂(6)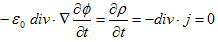
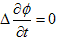 丂丂丂(7)
丂丂丂(7)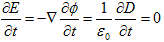 丂丂丂(8)
丂丂丂(8)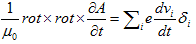 丂丂丂(9)
丂丂丂(9)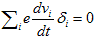 丂丂丂(10)
丂丂丂(10)
 丂丂丂(12)
丂丂丂(12) 丂丂丂(13)
丂丂丂(13)
 丂丂丂(13)
丂丂丂(13)
