NO.1883 無限級数の美しさ2 2010.10.24. 水の流れ
先日、青土社出版「πとeの話」を読んでいたら、無限級数の美しさと不思議さを見つけました。
皆さんに紹介します。2回目です。

注:この記事に関する投稿の掲載は、2010年11月8日以降とします。
NO.1882 無限級数の美しさ(2) 2010.10.24. 夜ふかしのつらいおじさん
(1-1)
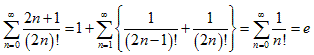
(1-2)
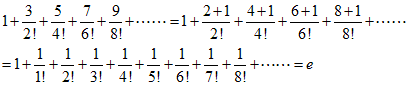
(2-1)
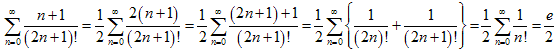
(2-2)
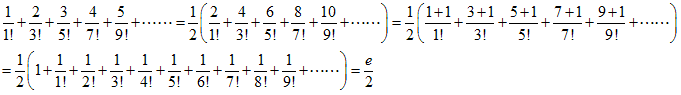
(3)次の関係式を使います。
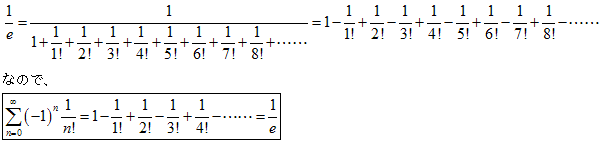
(3-1)
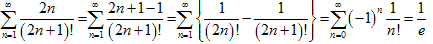
(3-2)
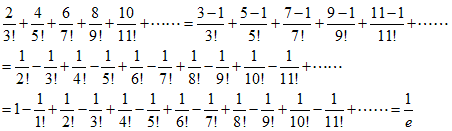
(4)
 について考えます。
について考えます。
まず、kの式に書き換え、k=1からk=nまでの部分和を考えます。

NO.1881 数論の問題(4) 2010.10.10. 数学マニア
自然数Nが、連続した自然数の和で表されるとすれば、最初の数をA、個数をnとして
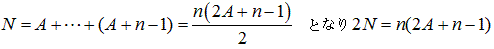
2Nの約数、全てを並べると(素因数に3が含まれていないときは3はいらない)、

n<2A+n-1 なので、上の行をn、下の行を2A+n-1 として対応させることができるが、
上と下のペアの数の和が偶数のときは、連続数としては表せない。
なぜなら n が奇数のとき、2A+n-1 は、偶数、
n が偶数のときは、2A+n-1 は、奇数でなければならないので、
必ずその和が奇数でなければならない。( Aを解くと整数にならない。
Aに有理数もゆるし、連続した数の意味を差が1とすれば、可能です。たとえば、
 が、2の冪数のみのときは、片方は、奇数なので、n=1 とすれば、連続した数の和とならない。
または、2A+n-1=1 とすれば、A>0 に反する( A<0の整数も許せば、2=-1+0+1+2 )上と下のペアの数の和が奇数のときは、上の数のかずだけ分割し、A、n を見つけることができ、連続数で表すことができます。上の数が、奇数のときは下の数は、必ず偶数になりますので可能です。上の数が偶数のとき、下の数は奇数となりつまりそれは奇素数のみの積の形となる。
が、2の冪数のみのときは、片方は、奇数なので、n=1 とすれば、連続した数の和とならない。
または、2A+n-1=1 とすれば、A>0 に反する( A<0の整数も許せば、2=-1+0+1+2 )上と下のペアの数の和が奇数のときは、上の数のかずだけ分割し、A、n を見つけることができ、連続数で表すことができます。上の数が、奇数のときは下の数は、必ず偶数になりますので可能です。上の数が偶数のとき、下の数は奇数となりつまりそれは奇素数のみの積の形となる。
したがって奇数の約数のかずだけ
分割の仕方があります。よって、Nが2の冪数のときは、奇数の約数はありませんので、連続した和では表せません。
奇数1を約数とするときは、1個の連続した分割として特別な場合として考えれば、奇数の約数のかずだけ分割の数があります。
一般に、その数自身も1個の連続した表しかたとして数えると、
N=2αP1β・・・Pkγ
(Pkは、奇素数)のとき、
(β+1)・・・(γ+1)は、表し方の個数となる。
例
N=180=223251 のとき、(2+1)(1+1)=6通りある。
| 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 | 10 | 12 | 15 | 18 |
| 360 | 180 | 120 | 90 | 72 | 60 | 45 | 40 | 36 | 30 | 24 | 20 |
(1,360),(3,120),(5,72),(8,45),(9,40),(15,24) の場合が可能で
2N=n(2A+n-1 )より、nとAを求めると、
(1,360)のとき、n=1、A=180
(3,120)のとき、n=3、A=59、59+60+61=180
(5,72)のとき、n=5、A=34、34+35+36+37+38=180
(8,45)のとき、n=8、A=19、19+20+21+22+23+24+25+26=180
(9,40)のとき、n=9、A=16、16+・・・+24=180
(15,24)のとき、n=15、A=5、5+・・・+19=180
Nが、n個の連続した和に分割できるとき。

NO.1880 三角形の回転問題(2) 2010.10.10. 夜ふかしのつらいおじさん
正三角形に近づくことをいいます。
●1.まず、三角形の性質の確認をします。(図1)
○三角形の二辺の和は他の一辺より長く、他の二辺の差より短いです。
つまり、a+b>c>a-b
○向かい合う頂点と辺に同じ文字を用いれば、角の大小と、辺の大小は同じになります。
つまり、∠B>∠A>∠C なら b>a>c です。

●2.次に正三角形になったときの状態をみておきます。(図2)
各点を回転しても隣の頂点に重なり図形の変化はありません。
●3.さて、一般的なときの様子を見てみます。
α、β、γのかわりに、A、B、Cを使います。
添字1の点を回転した点が添字2になっています。
不等辺の鋭角三角形A1B1C1において、辺B1C1=a1、C1A1=b1、A1B1=c1とおきます。
○1.△A1B1C1で、b1>a1>c1とします。(最長はb1、最短はc1とします)(図3)

△A2C1B2において、A2C1=b1、A2B2=c2、C1B2=(b1-c1)より、
(b1-c1)>b1-c2なので、c1<c2です。
もとの三角形で辺C1A1(b1)が最長なので、△A2C1B2において、
内角B2は鈍角になりその対辺A2C1(b1)が最長です。
よって、b1>c2となります。
つまり、b1>c2>c1となります。
△B2C2A1において、B2C2=a2、B2A1=c1、C2A1=(a1-c1)より、
(a1-c1)>a2-c1なので、a1>a2です。
もとの三角形が鋭角三角形なので、△B2C2A1において、
内角A1が鈍角になりその対辺B2C2(a2)が最長です。
よって、a2>c1となります。
つまり、a1>a2>c1となります。
△A2B1C2において、C2A2=b2、C2B1=a1、A2B1=(b1-a1)より、
(b1-a1)>b2-a1なので、b1>b2です。
もとの三角形が鋭角三角形なので、
△A2B1C2において、内角B1は鈍角になり対辺A2C2(b2)が最長です。
よって、b2>a1となります。
つまり、b1>b2>a1となります。
○2.△A1B1C1で、b1>c1>a1とします。(最長はb1、最短はa1とします)(図4)
その1と同様に考えると、
b1>c2>b1、c1>a2>a1、b1>b2>a1
となります。
以上をまとめると、各点を回転させると、各辺の最大と最小の差が小さくなると言うことです。

各辺の最大と最小の差が小さくなるということは、
操作を繰り返すたびに正三角形に近づくということです。
(正三角形に収束するかどうかは以上からはいえていません)
●4.二等辺三角形や鈍角三角形のときの補足

○左の図は頂角B1が108°より大きな二等辺三角形です。
a2がa1と同じ長さになります。
回転により、最大は変わらず最小が大きくなります。
○中の図は頂角が108°の二等辺三角形です。
回転により、最小は変わらず最大が小さくなります。
○右の図は頂角が108°より大きな鈍角三角形です。
回転により、最小がもとより小さくなりますが、最大がその分よりもっと小さくなります。
●5.お話

上の解答で正三角形に近づくことは確かですが、正三角形に収束するかは分かりません。
もとの三角形A1B1C1で辺の最大と最小の差は、図6(b1>a1>c1のとき)ではC1B2です。
回転した三角形A2B2C2で辺の最大と最小の差は、図6(b2>a2>c2になっている)では、b2-c2です。
この値は、
b2-c2<b1-c2=C1D<C1H=b1-c2=(b1-c1)×cos(∠C1)
として、(b1-c1)×cos(∠C1)で抑えられます。
もとの三角形A1B1C1で最小の内角はC1です。
回転後の三角形A2B2C2で最小の内角はC1よりも大きくなります。(余弦の値は小さくなる)
図3のパターンで、最大と最小の差は、b2-c2、b2-a2、c2-a2の場合がありえます。
それらが、図のC1Hで抑えられれば、正三角形に収束するといえます。
NO.1879 無限級数の美しさ 2010.10.3. 水の流れ
先日、青土社出版「πとeの話」を読んでいたら、無限級数の美しさと不思議を見つけま
した。皆さんに紹介します。
さらに、イギリスの数学者ハーデイー(1877~1947)の言葉も
ありました。書いてみます。
「数学者の思考様式は、画家や詩人のそれと同じように美しくなければならず
そのアイデアは、色や言葉と同じように調和を形作らなければならない
美は、なにものにも優先する試金石である
見苦しい数学がこの世で永遠に生命を保つことなどありえない」

注:この記事に関する投稿の掲載は、2010年10月18日以降とします。
NO.1878 積が和の2010倍(2) 2010.10.3. 夜ふかしのつらいおじさん
2数A、Bについて、積が和の定数 p1p2・・・pn 倍になるように考えます。
(各因数 p1,p2,・・・,pn は素数とします)
つまり 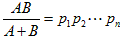 です。
です。
Ⅰ まず一般的に考えます。
(1)まず、各因数 p1,p2,・・・,pn がすべて数Aに含まれている場合を考え、
A= p1p2・・・pn a とします。
すると、 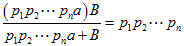 です。
です。
少なくとも a が約分できる形を考え、B=abとします。
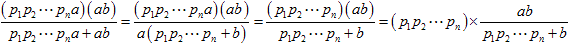
これから、 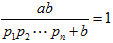 になるように考えます。
分母を払って ab=p1p2・・・pn +b
になるように考えます。
分母を払って ab=p1p2・・・pn +b
定数 p1p2・・・pn について解くと、
p1p2・・・pn=(a-1)b となります。
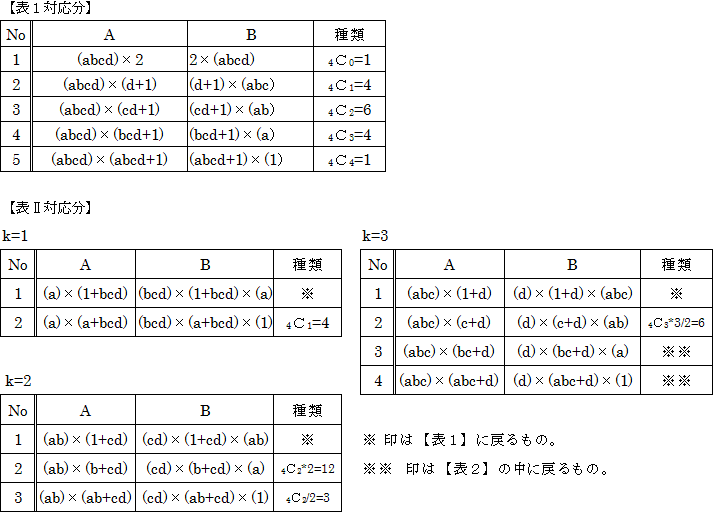
以上からA、Bについて整理すると、次の表1のようになります。

(2)次に、各因数 がA、Bに分かれて含まれている場合を考え、
A= p1p2・・・pk a、B= pk+1pk+2・・・pn b とします。
すると、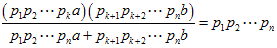 です。
です。
少なくとも a が約分できる形を考え、b=ab' とします。
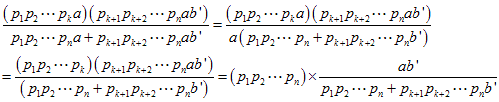
これから、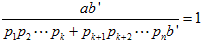 になるように考えます。
になるように考えます。
分母を払って ab'= p1p2・・・pk + pk+1pk+2・・・pn b
定数 p1p2・・・pk について解くと、
p1p2・・・pk
=(a-pk+1pk+2・・・pn)b'
となります。
以上からA、Bについて整理すると、次の表2のようになります。
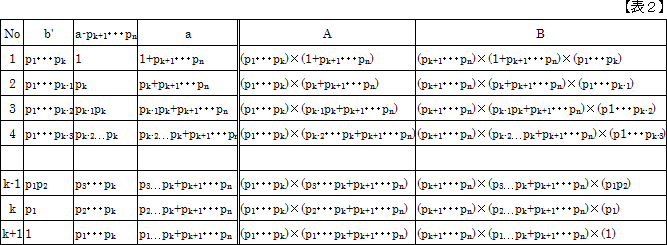
※ この表のNo1は(1)と実質的に同じものです。
(※ k=nとすれば、(1)の場合になりますが。)
Ⅱ 次に具体的に2010倍になる場合を考えます。
2010=2×3×5×67なので、Ⅰの場合のn=4のときです。
各因数 の代わりに、a,b,c,dで表します。
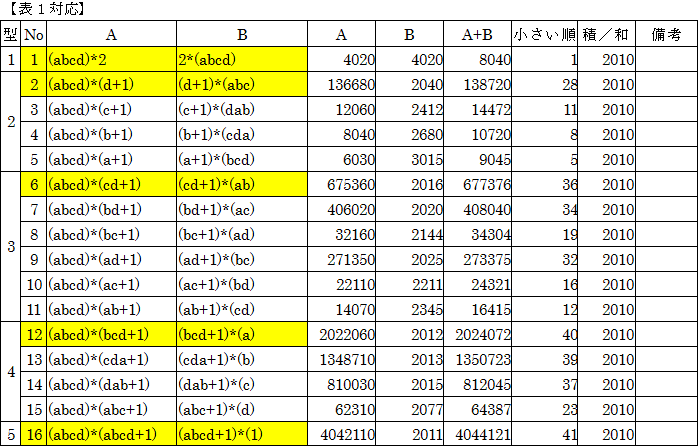
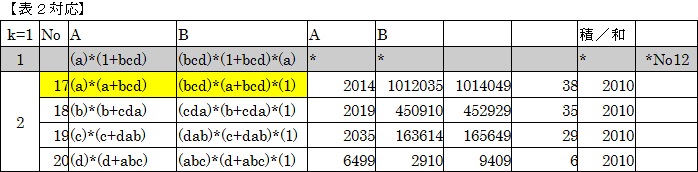
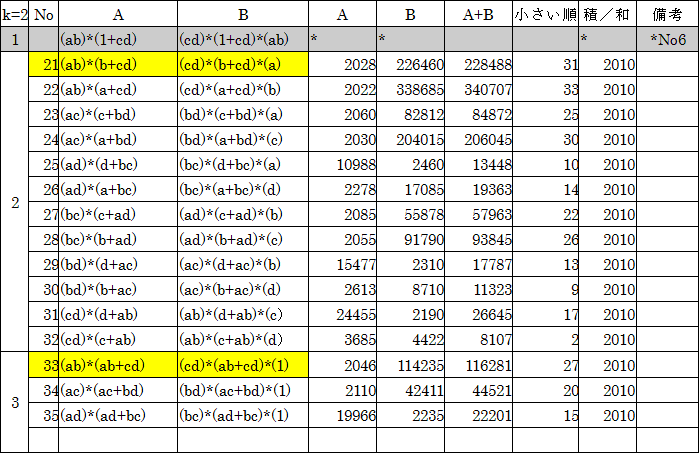
a=2,b=3,c=5,d=67とし計算すると、次のようになります。
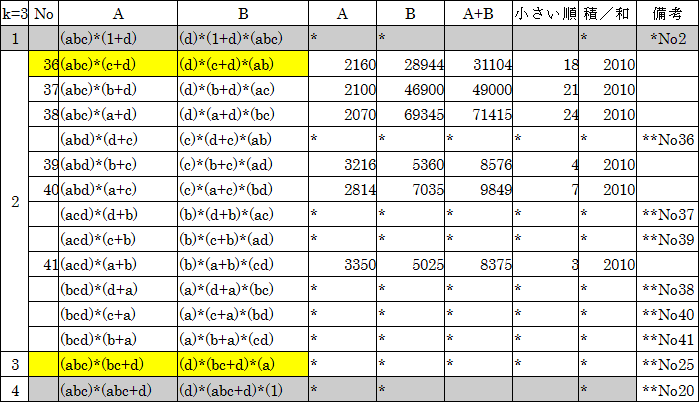
以上から、
問1 多分41組。
問2 和が最小は、No1の(4020,4020)、最大は、No16の(4042110,2011)
問3 上の表参照。
問4 2010=2*3*5*67は難しいので、2010にこだわらないで、1001=7*11*13ぐらいで充分だと思います。
