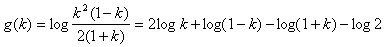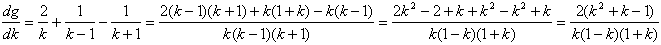NO.1709�@�@ �������㐔�������ƒ��z�� �@�@2008.1.28�@�@K.F.
�ꕔ�C���@1.29.23:00
�������L�����Ɩ���������Ȃ邱�Ƃ́A���Z���Ȃ�m���Ă��܂��B���������㐔�I(����)����
���z������Ȃ邱�Ƃ́A���Ȍn�̐��w���D���ȑ�w���Ȃ�m���Ă��܂��B
�����ő㐔�I���Ƃ́A�L���W���㐔������
�@�@�@anxn+an-1xn-1+���+a1x+a0=0(n��1,an��0���eai�͗L�����j�@�@�@�E�E�E��.1
�̉��ƂȂ鐔�̂��ƂŁA�S�Ă̗L��������� 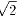 �Ȃǂ̖�����������ɂ�����܂��B
�Ȃǂ̖�����������ɂ�����܂��B
����A���z���Ƃ́A��.1�̑㐔�������̉��ƂȂ�Ȃ��悤�Ȏ���(���m�ɂ����Ε��f��)�̂��ƂŁA
��\�I�Ȓ��z���ɂ́A�l�C�s�A������~����������܂��B
�܂��A���Z�Ŋw�� 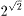 �����z���ł��B
�����z���ł��B
�Ƃ��낪�A�����ł����㐔�I���Ƃ́A�����܂Ŏ�.1�̑㐔�������̎������u�L���v�̏ꍇ�̉��ƂȂ�
���̂��Ƃł����āA�������u������v�̏ꍇ�ɂ́A���̉������z���ƂȂ�ꍇ������܂��B
���������ƁA�O�p�� sin x ��Taylor�W�J����A
�@�@�@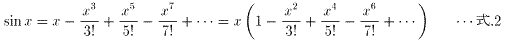
�ƂȂ�܂����A sin x=0 �Ƃ������������l����ƁA���̉��́A
�@�@�@x=0,�}��,�}�Q��,�}�R��,�E�E�E
�ƂȂ�܂��B�Ƃ����Ƃ́A
�@�@�@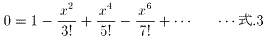
�Ƃ���������������̑㐔�������̉��́A�}��,�}�Q��,�}�R��,�E�E�E�Ƃ������ƂɂȂ�A
�S�Ē��z���ɂȂ�܂��B
�L���W���Ő��藧���Ƃ��A�����W���ł͐��藧���Ȃ����Ƃ́A
�J���g�[���̏W���_�ɂ��A�悭�m���Ă��܂��B
�܂��A������̑���������A��K�ƃR���p�X�����ŗ^����ꂽ�p�̂R�������ł��܂��B
�������Ă݂�ƁA�����Ƃ����T�O�́A�l�Ԃ��l�����ł������[���T�O���Ƃ��Â��v���܂��B
�Ƃ���ŁA���̖��́u�t�v�͐��藧�̂ł��傤���H�@���Ȃ킿�A�u�S�Ă̒��z���v�͎������������
�㐔�������̉��Ƃ��ĕ\�����̂ł��傤���H�@�����[�����ł��B
���NjL��
��.2�`��.3�̌��ʂ���A
�@�@�@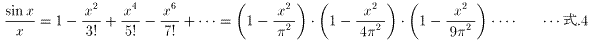
�Ə����\����邱�Ƃ��킩��܂��B�����ŁA��.4�̉E�ӂ�W�J���Ax2�̍����r����ƁA
�@�@�@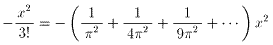
�ł��邱�Ƃ��킩��A
�@�@�@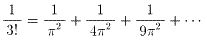
�����藧���Ƃ���A
�@�@�@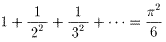
�ł��邱�Ƃ��킩��܂��B
��������ɋ����[�����Ƃł��B
NO.1708�@�@�K�E�X�̊i�q�_���@�@2008.1.28�@�@���̗���
�ꕔ�C���@1.31.23:00
��Q�O�R�w�I�ȉ�����
�F����A2007�N�x��w�������W�i�����o�Łj�ɂ����s�哌����w�̓�������
�Q�l�ɂ��Ď��̖������܂����B
�Ȃ��A�R�吔�w�҂̈�l�ł���h�C�c�̃J�[���E�t���[�h���q�E�K�E�X�i1777�`1855�N�j
�����̋Ɍ��l�����߂Ă��܂��B

���F���̋L���Ɋւ��铊�e�̌f�ڂ́A�Q�O�O�W�N�Q���P�W���ȍ~�Ƃ��܂��B
NO.1707�@�@ �g���`�F���̖��(2)�@�@2008.1.28�@�@��ӂ����̂炢��������
���̖��̃q���g�́A���V�U�̉E����15�i�y���l�|���FToru�j�����̕��ł��B
���
�O�p�`�`�a�b�Ŋp�`,�p�a,�p�b���P�Q�O�x�̎��A
�`�o�{�a�o�{�b�o���ŏ��ɂȂ�悤�ȎO�p�`�̓����̓_�o�́A
�p�`�o�a���p�a�o�b���p�b�o�`���P�Q�O�x�ƂȂ�_�ł���B
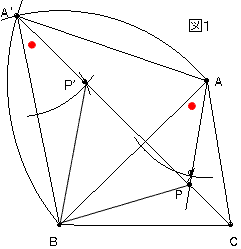
���P
�}�P�Ł�A�fBP�f��B�𒆐S�Ƃ��ā�ABP�����ւU�O����]�������̂ł��B
�o�`�{�o�a�{�o�b���ŏ��ƂȂ�ꍇ�́A�`�f�o�f�o�b���꒼���ɂȂ�ꍇ�ł��B
�Ȃ��Ȃ�A��PP�fB�����O�p�`�Ȃ̂�
PA�{PB�{PC��A�fP�f�{P�fP�{PC�ƂȂ邩��ł��B
(1)�o���ȒP�ɂƂ���@�́A�`�f�Ƃb�Ƃ����сڂa�`�f�b�Ɠ������`�a����Ƃ���
�p���Ƃ蒼���`�f�b�Ƃ̌�_���o�Ƃ�����@�ł��B
(2)�A���̕��@�́A�a����`�f�b�ɐ����a�g�����낵�܂��B�i�}�Q�j
�����āA�a�g�̒������@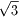 �@�Ƃ����O�p�`���Q�d�˂ĕH�`�������i�}�R�j
���̒����ق��̑Ίp���̎O�����̒��������g����b�ɐi�_���o�Ƃ�����@�ł��B(�}�S�j
�Ȃ��Ȃ�A���O�p�`BPP�f��BH���@
�@�Ƃ����O�p�`���Q�d�˂ĕH�`�������i�}�R�j
���̒����ق��̑Ίp���̎O�����̒��������g����b�ɐi�_���o�Ƃ�����@�ł��B(�}�S�j
�Ȃ��Ȃ�A���O�p�`BPP�f��BH���@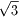 �@�Ƃ���Ɛ}�P���P�ӂ̒������Q�ƂȂ邩��ł��B
�@�Ƃ���Ɛ}�P���P�ӂ̒������Q�ƂȂ邩��ł��B
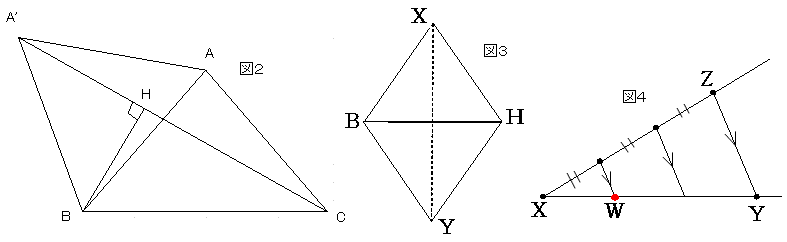
�}�S��X��ʂ�K���Ȓ���XZ�������A���Ԋu�ɂR�̓_�����
XY�ƕ��s�ɓ��Ԋu�̓_��ʂ钼����������XW���P�̑傫������B
(3)�炵�������́A�_�o�����`�a�b�̊e�ӂ��P�ӂƂ��鐳�O�p�`�̊O�ډ~�̌�_�Ƃ�����@�ł��B�i�}�T�j
���O�p�`�`�a�i�̊O�ډ~�Ɛ��O�p�`�`�b�g�̊O�ډ~�̌�_�ł`�łȂ����̓_���o�Ƃ��܂��B
�l�p�`�i�a�o�`�͉~�ɓ��ڂ���̂Łڂa�o�`���P�Q�O���ł��B
�l�p�`�g�`�o�b�͉~�ɓ��ڂ���̂Łڂb�o�`���P�Q�O���ł��B
����ƁA�l�p�`�f�b�o�a�̓��p�b�o�a���P�Q�O���ɂȂ�܂��B
�l�p�`�f�b�o�a�͌����������Q�̓��p�̘a���P�W�O���ɂȂ�̂ʼn~�ɓ��ڂ��܂��B
�ȏォ�灢�`�a�b�̊e�ӂ��P�ӂƂ��鐳�O�p�`�̂R�̊O�ډ~�͂P�_�Ō����܂��B
�ڂi�o�a�͌�B�i�ɂ��~���p�Ȃ̂łU�O���ł��B
����ƁA�ڂi�oB�{��B�o�b���P�W�O���ƂȂ�A�R�_�i�A�o�A�b�͓��꒼����ɂ���܂��B
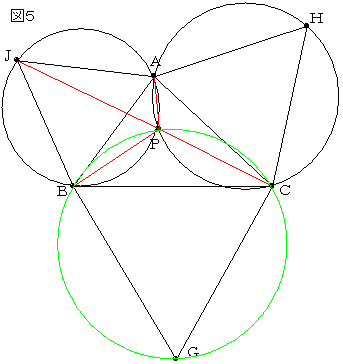
�_P�͎O�p�`ABC�̊e���_�ƌ��ԂƁA�R�U�O�����R���������ꂼ��̊p�͂P�Q�O���ɂȂ�܂��B
���Q
�o�`�{�o�a�{�o�b�̒����̍ŏ��l�́A�_�`�����ւU�O����]�ړ������_�`�f�Ƃb�Ƃ̋��������߂�悢�B
�_�`�f��
����Ăo�`�{�o�a�{�o�b�̒����̍ŏ��l��
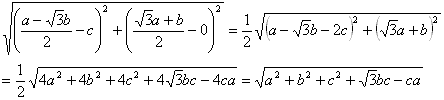
���R
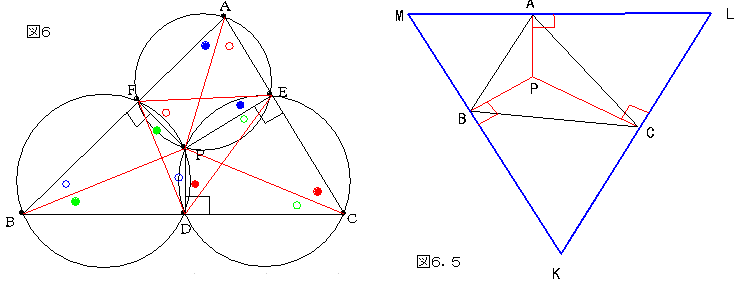
���`�a�b�̓����̓_�o����e�ӂɂ��낵�������̑��������c�d�e�͐��O�p�`�ɂ͂Ȃ�܂���B
�o�`�{�o�a�{�o�b�̒l���ŏ��ɂȂ�ꍇ�́A�ڂ`�o�a���ڂa�o�b���ڂb�o�`���P�Q�O���̂Ƃ��ł��B
���o�`�a�A���o�a�b�A���o�b�`�͒��_�o�̂Ƃ���̓��p�͂P�Q�O���Ȃ̂ŁA���̓��p�̘a�͂U�O���ł��B
�}�œ����F�̊p�i���Ɓ��j�̘a�͂U�O���ł��B
���c�d�e�̓��p�͐}�̂悤�ȗl�q�ɂȂ��Ă��܂��B�i���_�ɏW�܂�p�̐F���Ⴄ�j
�������ʂɂ́��c�d�e�̓��p�͂��ꂼ��U�O���ɂ͂Ȃ�܂���B
�����Ȃ�̂͂��Ƃ��Ƃ́��`�a�b�����O�p�`�̂Ƃ��ł��B
����̕��͊ȒP�ł��B
�Ⴆ�A�l�p�`MBPA�́�A�Ɓ�B�̘a���P�W�O���Ȃ̂ʼn~�ɓ��ڂ��܂��B
��APB���P�Q�O���Ȃ̂Ł�M�͂U�O���ƂȂ�܂��B
���S
�����`�̏ꍇ�A�o�`�{�o�a�{�o�b�{�o�c�i������j�̒l���ŏ��ɂȂ�͓̂_�o���Ίp���̌�_�ɂȂ�ꍇ�ł��B
�_�o���Ίp���̌�_���͂����ƁA�Ίp�����ӂƂ���O�p�`���l���āA�i���j���K���傫���Ȃ�܂��B
�@�@�@�@�o�f�`�{�o�f�a�{�o�f�b�{�o�f�c
�@�@�@���o�f�`�{�o�f�b�{�o�f�a�{�o�f�c
�@�@�@���`�b�{�a�c
�@�@�@���o�`�{�o�b�{�o�a�{�o�c
�@�@�@���o�`�{�o�a�{�o�b�{�o�c
NO.1706�@�@ �g���`�F���̖��@�@2008.1.7�@�@���̗���
�ꕔ�C���@1.8.20:30
��Q�O�Q�w�I�ȉ�����
�F����A�p�Y���łЂ�߂��⏕���̊w�i�����`�쒘�j�u�u�k�Ёv��ǂ�ł����Ƃ���A
���̂悤�Ȗ����������̂ŁA�Q�l�ɂ��Ė������܂����B
�C�^���A�̕����w�҂ŁA�K�����I�E�K�����C�̒�q�������g���`�F���i1608����1647�j
�͊w��
�Ƃ��Ă��L���ł��������Ƃ������m�ł������B�t�����X�̑㐔�w�҃t�F���}�[�̓g���`�F����
�u�O�p�`�̊e���_����̘a���ŏ��ɂȂ�_�����߂�v�Ƃ��������o�������Ƃ�����A
�Ȍケ����g���`�F���̖��Ɠǂ�Ă��܂��B�������炪�A���ł��B
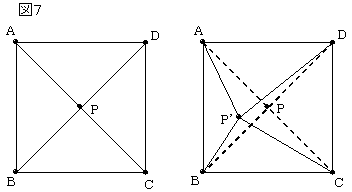
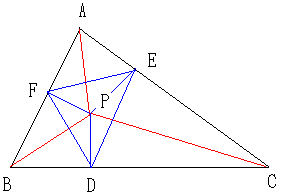
�O�p�`�`�a�b������B���̓����ɓ_�o���Ƃ��āA
�_�o�ƂR�̒��_�`�C�a�C�b��}�̂悤�Ɍ��т܂��B
���̂Ƃ��A�����̘a�o�`�{�o�a�{�o�b���ŏ��ɂ���_���o�Ƃ���B
�������A�O�p�`�`�a�b���݊p�O�p�`�̏ꍇ�A�݊p�̑傫���͂P�Q�O�x�����Ƃ���B
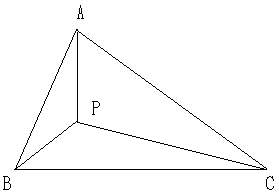
���P�F�_�o���ǂ��ɂƂ�悢�ł��傤���B
�q���g�F�o�`�{�o�a�{�o�b�Ɠ��������̐܂�������悤�ɁA
���_�a�𒆐S�ɂ��āA�O�p�`�`�o�a���U�O�x��]�����Ă��������B
�������A���̉�@������܂��B
���Q�F�R�̒��_�̍��W���`�i���C���j�A�a�i�O�C�O�j�A�b�i���A�O�j�Ƃ����Ƃ��A
�o�`�{�o�a�{�o�b�̍ŏ��l�����A���A���ŕ\���B
���R�F�_�o����R�ӂ��������낵���Ƃ��̑���}�̂悤�ɁA�c�A�d�C�e�Ƃ����Ƃ��A
�����O�p�`�c�d�e�����O�p�`�ɂȂ�Ƃ���T�C�g�ɏ����Ă���܂����B
���̏ؖ���������܂����Ă��������B
���j
���3�Ɋւ��āA��DEF���O�p�`�ɂȂ�Ȃ��̂ł͂Ȃ����ƁA�w�E������A
�����g���Ԉ���Ă���̂ł͂Ȃ����ƁA�v���n�߂܂����B
�ڂ����͂����������Ă��������B�i���̗���j
����ɁA
���S�F1�ӂ̒������P�O�����ł��鐳���`�`�a�b�c����B
�S���_�Ɏ��鋗���̘a���ŏ��ɂȂ�悤�Ȍo�H��}�Ŏ����Ă��������B
�܂��A���̍ŏ��l�����߂Ă��������B
�����F�O�p�`�`�a�b���݊p�O�p�`�ŁA�݊p�̑傫�����P�Q�O�x�ȏ�̂Ƃ��A
�o�`�{�o�a�{�o�b���ŏ��ƂȂ�_�o�͂��̓݊p�ł��钸�_�ɂȂ�܂��B
���F���̋L���Ɋւ��铊�e�̌f�ڂ́A�Q�O�O�W�N�P���Q�W���ȍ~�Ƃ��܂��B
NO.1705�@�@�Z�zin�{��(3)�@�@2008.1.7�@�@��ӂ����̂炢��������
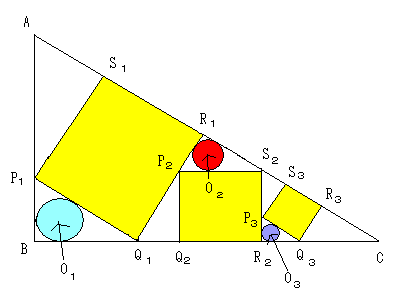
�����������邾���Ȃ�A����Ȃɓ������܂���B
��ABC�Ɓ�Q�PR�PC�͑����ł��B
���́�Q�PR�PC�Ɓ�S�QR�QC�������ŁA�����̔� p �������ł��B
�~O�P�Ɖ~O�Q�͑����ł��B
���̉~O�Q�Ɖ~O�R�������ő�����͏�̎O�p�`�Ɠ��� p �ł��B
������ 25p2��16 ��� p��0.8 �Ȃ̂ŁA�n2�̒��a�́A25�~0.8��20cm
�܂��A���P�A���Q�A���R �͂��̏��ɓ��䐔����Ȃ��̂ŁA
�i���Q�j2�����P�~���R
���āAO�P�̒��a��25cm�ƂȂ�̂͂ǂ�ȏꍇ�����ׂĂ݂܂��B
�O�p�`�̏c���̒����̔䂪������悢�̂ŁA�}�Q�̂悤�ɉ����P�A�c�����Ƃ��܂��B
������ BE���� �Ƃ���ƁADB������
DE2=DG2 ���
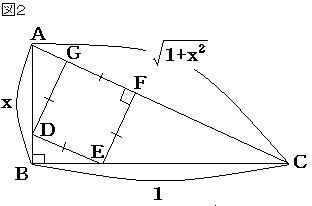
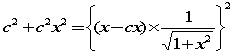
��������
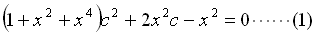
�����O �ɒ��ӂ��āi�P�j�� �� �ɂ��ĉ�����
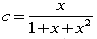
����ƁACE=1-c �A������� 0.8 �Ƃ���
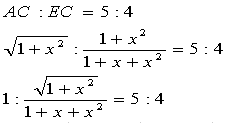
 ��������
��������
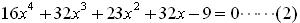
���̕������̉��̂������̎��������߂��
�@�@�@���� 0.2297766
�����
�@�@�@BE=����0.17915272
�@�@�@BD=cx=0.041165103
�@�@�@DE=0.183821279
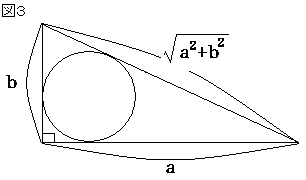
�����Œ��p�O�p�`�ɓ��ڂ���~�̔��a �� �ɂ��Ē��ׂ܂��B
�ʐς��ʂ�ŕ\���Ă݂�Ɓi�}�R�j
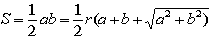
��������
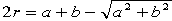
�i�܂�A�c���̘a����Εӂ����������́j
�}�Q�̒��p�O�p�`�ɑ��ẮA
�@�@�@2���� 0.036497(���悻�̒l�j
���ꂪ25cm�ɂȂ�̂�����A���ۂ̉��̒�����L�Ƃ����
�@�@�@0.25�FL��0.036497�F1
�@�@�@L=6.849964(���悻�̒l�j
�@�@�@�c��1.573961(���悻�̒l�j
���ۂɂ͎��̂悤�Ȋ����̒��p�O�p�`�ɂȂ�܂��B
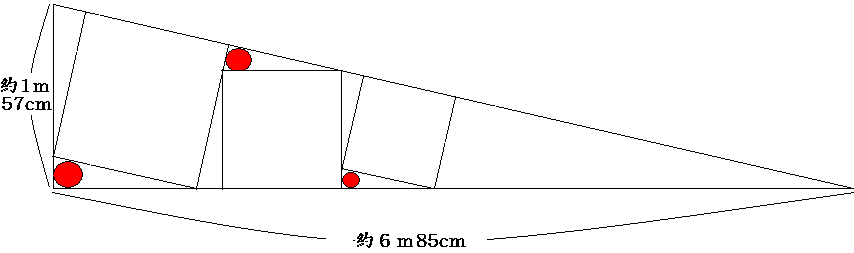
NO.1704�@�@�Z�zin�{��(2)�@�@�@2008.1.7.�@�@teki
�}�̉~O�P�AO�Q�AO�R�͑S�Đ����`�Ƒ����ɂȂ��Ă���A
���̖ʐς�O�P�FO�Q��O�Q�FO�R�@�ł��B
����āAO�Q�~O�Q��O�P�~O�R�@�̊W���������܂��B
�܂�Ԃ��~�̒��a�͂Q�O�����Ƃ������Ƃ��킩��܂��B
��ʓI�ɂ͒��a�����P�A���Q�A���R�Ƃ���ƁA
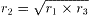 �Ƃ����W���������܂��B
�Ƃ����W���������܂��B
NO.1703�@�@�u���w�K�[���v�@�@�@2008.1.3.�@�@Junko
�{�₳��Ŗڂɂ�������_���u���w�K�[���v��ǂ�ł��܂��B
�^���ɖ₢�𓊂������Ă����y�̌��C�����e�g�������ƁA
�G���K���g�ȉ�@�Ŏ�l����ł��̂߂��˕Q�~���J�����A
�����č��Z���̎�l�����A�l�X�Ȑ��w�Əo��A
���̔閧�������������Ă����܂��B
��������邱�ƂȂ���A�t�B�{�i�b�`�����[�[�^���ȂǁA���͓I�Ɍ���Ă����܂��B
����ɂ��Ă��A�e�g�������ƃ~���J�����A�Ō�͂ǂ��Ȃ�̂��ȂƋC�ɂȂ�Ƃ���ł��B
NO.1702�@�@ NO.1695�͉��́H �@�@�@2008.1.3.�@�@�c�c�s
NO.1695�̓����́A�`�o�F�o�a�͉����䂪�����Ǝv���܂����A���̂Ȃ�ł��傤�H
��m�b�̏��������ł���������A�Ȃ�炩�̗��R��������Ȃ����̂��H�ƁA����Ă݂܂����B
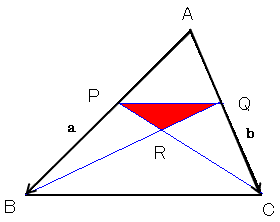 NO.1697�Ɠ��l�ɁA�`�a���x�N�g��a�C�`�b���x�N�g��b�Ƃ��A
a�Cb�ʂ̊��ɂƂ�܂��B�`�o��ka�C�`�p��kb�C0��k��1�Ƃ��܂��B�܂����(a�Cb)�����W���Ƃ���A
���W��ԂɈڂ��Ă݂܂��B
NO.1697�Ɠ��l�ɁA�`�a���x�N�g��a�C�`�b���x�N�g��b�Ƃ��A
a�Cb�ʂ̊��ɂƂ�܂��B�`�o��ka�C�`�p��kb�C0��k��1�Ƃ��܂��B�܂����(a�Cb)�����W���Ƃ���A
���W��ԂɈڂ��Ă݂܂��B
���Ƃ̃��[�N���b�h��ԁi���ʁj�ɂ�������́A
�@�@�@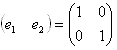
�Ƃ����܂��B
���Ƃ̃��[�N���b�h��Ԃɂ�������W�l�i�\���x�N�g���j��(x�Cy)�Ƃ��A
���(a�Cb)�Ɉڂ����Ƃ��̍��W�l��(k�Cl)�Ƃ���ƁA
�@�@�@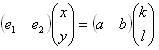
�ł��B���͖ʐϔ�Ȃ̂ŁA(a�Cb)�����x�N�g���Ƃ��āA
(e1�Ce2)�ɂ���ĕ\���鎖�ɒ��ӂ���ƁA���R�r�A���ɂ��A
�@�@�@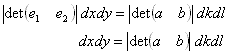
�ƕ\���鎖���킩��܂��B�����ŁA|det(a�Cb)|�́A(k�Cl)�ɂ��Ȃ��萔�ł��B
�]���āA���}�̂悤�ȏ�ԂɈڂ��Ă��A���`�a�b�Ɓ��o�p�q�̖ʐϔ�͕ς��܂���B
���}�ɂ����āA(x�Cy)��Ԃ���(k�Cl)��ԂɈڂ��Ă��A�����`�a�C�a�b�C�o�p�Ȃǂ������ł��葱����̂́A
��L���ϊ����A��̒萔���̊Ԃ̐��`�ϊ��ł��邩��ł��B
�]���ĖʐϊԂł��A�萔���ۂ��܂��B
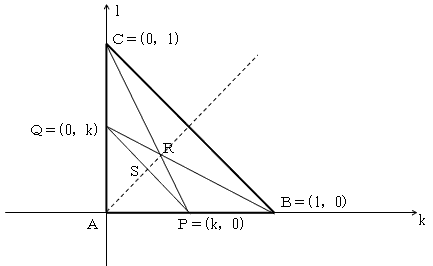
�����łq��(k�Cl)���W�ł����ANO.1697���A
�@�@�@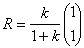
�ł��i(k�Cl)��Ԃ̍��W���g���Ē��ڌv�Z���Ă������ł��j�B
���ɂo�p�̒��_�r��(k�Cl)���W�́A(k�Cl)��ԂŒ��ڌv�Z���Ė��炩�ɁA
�@�@�@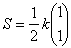
�ƂȂ�܂��B(k�Cl)��Ԃɂ���̂ŁA�o�p�Ƃq�r�͒������܂��B
����āA���o�p�q�̖ʐς́A
�@�@�@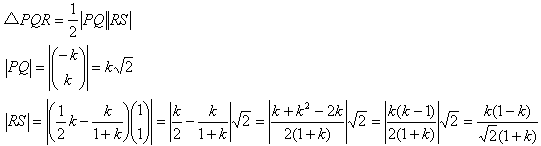
���A
�@�@�@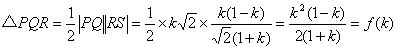 �@�Ƃ���B
�@�Ƃ���B
���v�Z�ł��܂��B�����ł́A0��k��1���g���Ă��܂��B
g(k)��log f(k)�Ƃ��āAf(k)�̍ő�l�������邽�߂ɁAg(k)��k�Ŕ�������ƁA
�@�@�@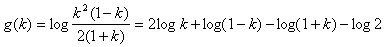
�Ȃ̂ŁA
�@�@�@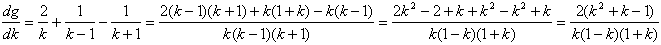
�������܂��B���̌��ʂƁANO.1697��g'(k)���r����Ǝ����I�ɓ����ł���A
���o�p�q�̖ʐς��ő剻����1�Fk�̒l�́A���`�a�b�̌`�ɗR��Ȃ����́A����Ŗ��炩�ɂ͂Ȃ�܂����A
���̉�����ɂȂ邩�́A����ς��ł��B
dg/dk�̕��q�ɂ����āAk2�|k�|1��0������邽�߂ɂ́A
�Ⴆ�����p�O�p�`�ɕW���������Ƃ��Ă��A��蕶�Ɍ����S�Ă̏������K�v�ł��B
���p�O�p�`�ɕW��������A�ǂꂩ�̏����͊O���̂ł͂Ȃ���
�i�W���`�ɏ����̈ꕔ�ɉ����ł���̂ł͂Ȃ����H�j�Ɗ��҂����̂ł����A�ʖڂł����B
�ł����R�͂���͂��ł��B�F����̈ӌ��������ł��B�ʖڂł��傤���H
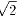 �Ȃǂ̖�����������ɂ�����܂��B
�Ȃǂ̖�����������ɂ�����܂��B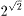 �����z���ł��B
�����z���ł��B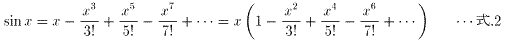
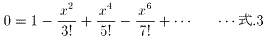
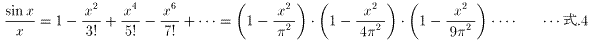
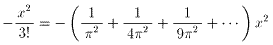
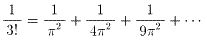
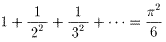


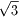 �@�Ƃ����O�p�`���Q�d�˂ĕH�`�������i�}�R�j
���̒����ق��̑Ίp���̎O�����̒��������g����b�ɐi�_���o�Ƃ�����@�ł��B(�}�S�j
�Ȃ��Ȃ�A���O�p�`BPP�f��BH���@
�@�Ƃ����O�p�`���Q�d�˂ĕH�`�������i�}�R�j
���̒����ق��̑Ίp���̎O�����̒��������g����b�ɐi�_���o�Ƃ�����@�ł��B(�}�S�j
�Ȃ��Ȃ�A���O�p�`BPP�f��BH���@

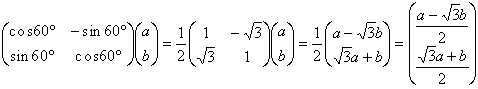
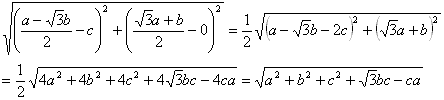






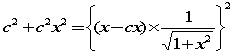
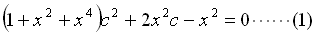
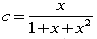
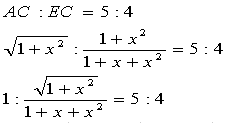
 ��������
��������
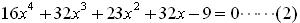
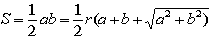
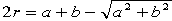

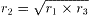 �Ƃ����W���������܂��B
�Ƃ����W���������܂��B
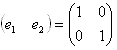
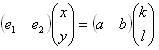
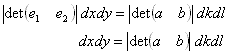

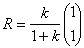
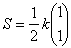
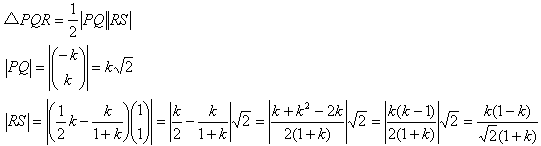
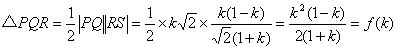 �@�Ƃ���B
�@�Ƃ���B