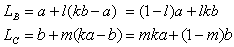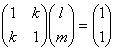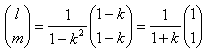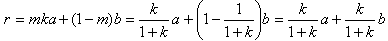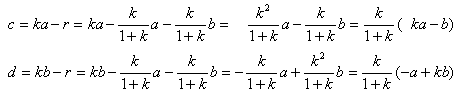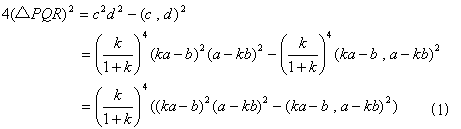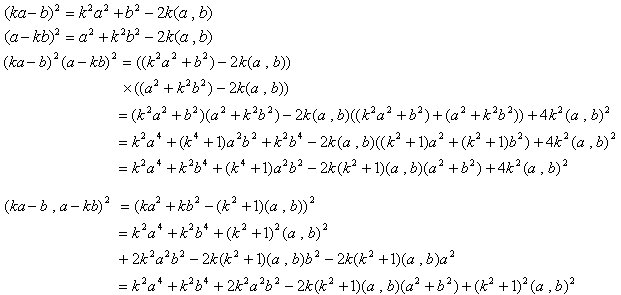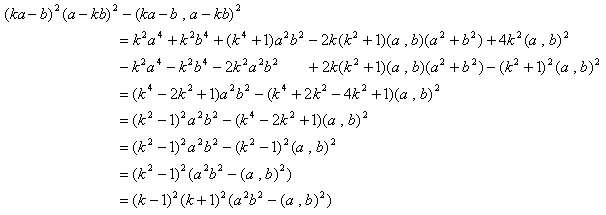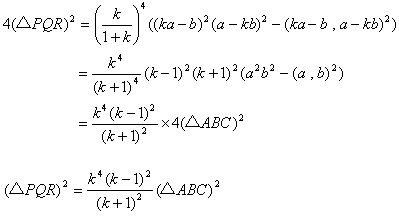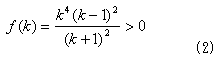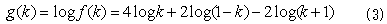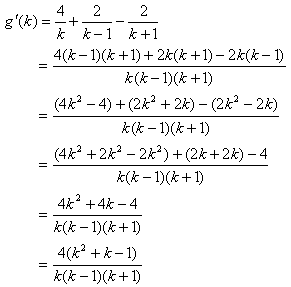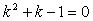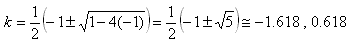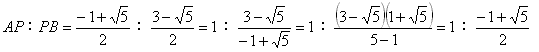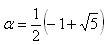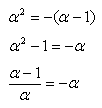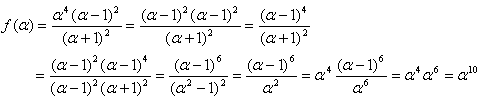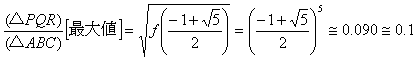NO.1701丂丂2.5儁乕僕偱傢偐傞検巕僐儞僺儏乕僞偺巇妡偗丂丂丂2007.12.25丂丂丂俢俢俿
儁儞儘乕僘偝傫偑乽怱偺塭乿偺拞偱丄
乽検巕僐儞僺儏乕僞偼挻暲楍壔偝傟偨僲僀儅儞僐儞僺儏乕僞偵夁偓側偄乿偲尵偄愗偭偰偔傟偨偍偐偘偱丄
検巕僐儞僺儏乕僞偺巇妡偗偑傢偐偭偨婥偑偟傑偡丅椺偵傛偭偰丄徻嵶偼柍棟偱偡偑
丅埲壓偼A4偱栺2.5儁乕僕偱偡丅
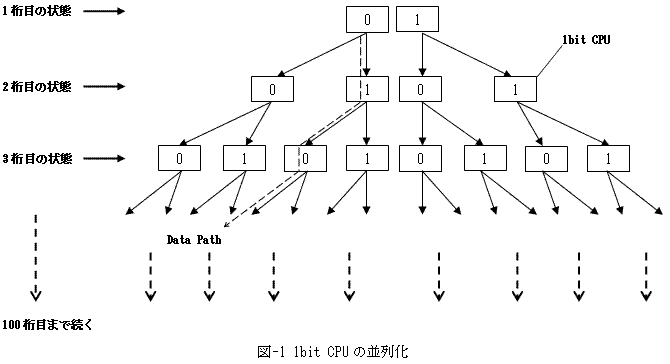
侾丏100寘偺2恑埫崋
偙偙偱偼丄偱偒傞偩偗忬嫷傪娙扨壔偡傞偨傔偵丄
100寘偺2恑埫崋傪夝偔忬嫷傪峫偊傑偡丅100寘偺2恑埫崋偲偼丄
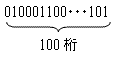
傒偨偄側0偲1偺暲傃偱偡丅
峫偊傜傟傞2100働乕僗偺01暲傃偺拞偱丄偨偭偨堦捠傝偑惓夝偩偲偟傑偡丅
巊梡偡傞僐儞僺儏乕僞偺CPU傕丄忬嫷傪扨弮壔偡傞偨傔丄
1bit CPU偩偲偟傑偡丅1bit CPU偑堦搙偵埖偊傞忬懺偼丄CPU偑0傪曐帩偡傞偐丄
1傪曐帩偡傞偐偺偳偪傜偐偱偡丅惓妋偵尵偆偲丄偙偆偄偆忬懺偺曐帩偼丄
CPU偺拞偺儗僕僗僞乕偲尵傢傟傞婎杮婡峔偱幚尰偝傟偰偄傑偡丅
巹偼8bit CPU偺帪戙偐傜杮奿揑偵僐儞僺儏乕僞偲晅偒崌偄偼偠傔丄
CPU偼16bit丆32bit偲恑壔偟偰偒傑偟偨丅傕偆偡偖64bit帪戙偺摓棃偱偡丅
8bit CPU偼儗僕僗僞乕傪8屄丆16bit偼16屄帩偭偰偄傑偡丅
側偺偱1bit CPU偲偼丄儗僕僗僞乕1屄偺CPU偺婎杮婡峔偦偺傕偺偱偡丅
尰嵼庡棳偺32bit CPU偼丄偙傟傛傝梱偐偵崅惈擻偱偡丅
俀丏CPU亊1偺応崌
僐儞僺儏乕僞偑1bit CPU亊1偺応崌傪峫偊傑偡乮嵟嬤棳峴偺Dual Core偱偼偁傝傑偣傫乯丅
1bit CPU偼100寘慡偰傪堦搙偵尒搉偣側偄偺偱丄
柧傜偐偵嵟埆100亊2100夞摦嶌偡傞昁梫偑偁傝傑偡丅
儊儌儕忋偵100bit偺椞堟傪妋曐偟偰偍偄偰丄偁傞100寘偺01楍傪僙僢僩偡傞偨傔偵丄
100寘偺01楍偺1僷僞乕儞偵偮偒丄儊儌儕偲100夞捠怣偟傑偡丅
偙傟偑100亊偺堄枴偱偡丅拲堄偡傋偒偼64bit CPU偩偭偰丄摦嶌夞悢偼偦傫側偵曄傢傜側偄偙偲偱偡丅
傢偐傝傗偡偔100bit CPU偩偲偡傞偲丄摦嶌夞悢偼2100夞偱丄
100bit CPU傛傝100攞懍偄偩偗偱偡
乮幚嵺偵偼丄偁傟傗偙傟傗偺柍懯偑徣偗偰悢10枩攞懍偄偲偼巚偄傑偡偑丄偄偢傟偵偟傠丄乯丅
2100偼1030偺僆乕僟乕偵偁傝丄100亖102(傗105)偺堘偄側偳熸偩偲傢偐傝傑偡丅
尰嵼偺昗弨婡偺搵嵹偡傞1GHz CPU偩偲偟偰扨弮寁嶼偡傞偲丄嵟埆偱丄
1030夞/109夞/60昩/60暘/24帪娫/365擔亖3.2亊1013擭偲側傝傑偡丅
俁丏2(2100-1)屄偺暲楍壔
偟偐偟1bit CPU偩偗傪巊偭偰丄CPU偺摦嶌1夞偱丄100寘偺2恑埫崋傪夝偔曽朄偑偁傝傑偡丅
2(2100-1)屄偺1bit CPU傪暲楍壔偝偣傟偽偄偄偺偱偡乮恾-1乯丅
恾-1偺1bit CPU偼慡偰摨帪偵摦嶌偡傞偲偟傑偡丅
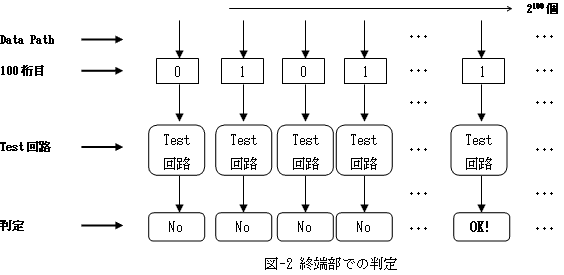
偦偟偰恾拞偺揰慄栴報偱帵偟偨Data Path偵増偭偰偦傟傜偼捠怣偟丄
2恑埫崋偺僥僗僩僷僞乕儞偑乽010ゥv偺傛偆偵丄Test夞楬偵僙僢僩偝傟傑偡丅
恾-2偼丄Data Path偵増偭偰弌棃忋偑偭偨僥僗僩僷僞乕儞偑丄Test夞楬偵擖傞條巕傪帵偟偰偄傑偡丅
榖傪扨弮壔偡傞偨傔偵丄Test夞楬傕昁梫側傜2100屄愝偗傞偲偟傑偡丅
恾-1丆2偐傜傢偐傞傛偆偵丄慡偰偺CPU偲Test夞楬偑棟憐揑偵摨帪偵摦偗偽丄CPU偺1夞偺摦嶌偱丄
100寘偺2恑埫崋偼夝偗傞偼偢偱偡丅1GHz偺CPU偩偲偡傟偽丄1壄暘偺1昩偱廔椆偱偡丅
栤戣偼丄偙偺傛偆側挻暲楍壔偼尰幚栤戣偲偟偰晄壜擻側偲偙傠偵偁傝傑偡丅
- 尰嵼偺僾儕儞僩婎斅媄弍傪傕偭偰偟偰傕丄1030偺僆乕僟乕偺CPU偲丄Data Path偱昞偝傟偨捠怣儔僀儞偺攝慄偼柍棟丏
- 尰幚偵偼捠怣懍搙乮婃挘偭偰岝懍埲壓乯偺栤戣偱丄慡晹偑摨帪偵摦偔傢偗偑側偄丏
- 偙傫側廤愊夞楬傪嶌偭偨傜丄偒偭偲擬偔側傝偡偓傞丏
側偳偱偡丅1030屄偲偄偆悢帤偑偳傫側偵偲傫偱傕側偄傕偺偐偼丄
扨弮寁嶼偱傕傢偐傝傑偡丅尰嵼偺婎斅媄弍偼丄
1cm2偺拞偵丄100枩僆乕僟乕偺僩儔儞僕僗僞乕側傫偐傪媗傔傜傟傞偲偙傑偱棃偰偄傑偡丅
僾儕儞僩婎斅偺岤傒偑1000暘偺1mm偲壖掕偟偰丄僒僀僐儘忬偺棫懱暲楍CPU傪峫偊傞偲丄
丂丂丂1030屄/106屄/10mm/1000屄亖1020cm3亖1014m3亖105km3亞46km亊46km亊46km
側傫偰帠偵側傝傑偡丅
係丏検巕CPU偺応崌
偙偭偐傜丄徻嵶偼柍棟側榖偵擖傝傑偡丅変揷堷悈偱怽偟栿側偄偱偡偑丄
NO.1515丆
NO.1521丆NO.1530偱埖偭偨僔儏僥儖儞丒僎儖儔僴幚尡偲EPR岠壥傪巚偄婲偙偟偰壓偝偄丅
傑偢屳偄偵媡岦偒偺僗僺儞乮椺偊偽偦傟傜傪亄丆亅偱昞偟傑偡乯傪帩偮2屄1慻偺揹巕傪敪惗偝偣傑偡丅
揹巕偺僗僺儞偼帴応傪敪惗偝偣傞偺偱丄2屄偺揹巕偼媡岦偒偺帴愇偱偡丅
偦偙偱2屄偺揹巕傪忋壓帴応偺拞偵捠偡偲丄堦曽偼忋岦偒偵丄懠曽偼壓岦偒偵嬋偑傝傑偡丅
偳偪傜偺揹巕偑偳偪傜偵嬋偑傞偐偼丄50亾偺妋棪偱偟偨丅偦偺屻偱崱搙偼嵍塃帴応偺拞傪捠偡偲丄
堦曽偼嵍岦偒偵丄懠曽偼塃岦偒偵嬋偑傝丄偳偪傜偵嬋偑傞偐偺妋棪偼丄崱搙傕50亾偱偡丅
偙傟偑僔儏僥儖儞丒僎儖儔僴幚尡偱偟偨丅
寢壥偲偟偰揹巕偺亇偼丄娤應偵傛偭偰寛傑傞偲偄偆忢幆偵斀偟偨寢榑偵側傝丄
堦曽偑亄偲娤應偝傟偨傜丄傕偆堦曽偼昁偢亅偱丄偙偺娤應帪偵婲偙傞亇偺寛掕岠壥偼丄
揹巕娫傪弖帪偵揱傢傝傑偡丅偄偔傜棧傟偰偄偰傕丅偙傟偑EPR岠壥偱偟偨丅
偄偔偮偐惂尷偼偁傞偺偱偡偑丄揹巕偺僗僺儞偵EPR岠壥偑惉傝棫偮側傜丄
揹巕偺憱傞岦偒偵偩偭偰EPR岠壥偑惉傝棫偭偰偄偄偼偢偱偡丅妋擣偟偰偍傝傑偣傫偺偱丄
師偺2抜棊偼堦庬偺斾歡偲偟偰偍暦偒壓偝偄丅
揹巕偺憱傞岦偒偲偼丄揹棳偺亇偱偡丅揹棳偺亇偵傛偭偰丄
CPU偼偦偺忬懺偑乽0乿偱偁傞偐乽1乿偱偁傞偐傪曐帩偟傑偡丅偦偆偡傞偲丄
傕偟丄CPU撪晹偺揹巕偺憱傞岦偒偵懳偟偰丄
EPR岠壥傪棙梡偱偒傞側傜丄恾-1偺乽1寘栚偺忬懺乿傪昞偡2屄偺CPU傪丄
1屄偺CPU偱幚尰偱偒傑偡丅NO.1515丆
NO.1521丆NO.1530偺偳偙偐偱弎傋偨傛偆偵丄
娤應偝傟傞傑偱偺検巕忬懺偼丄乽0乿偲乽1乿偺忬懺傪摨帪偵偲傟傞偐傜偱偡丅
僔儏僥儖儞丒僎儖儔僴幚尡偼忬懺偑2屄偲偄偆嬌抂側応崌偱偟偨偑丄
偨偔偝傫偺忬懺傪検巕揑偵摨帪偵偲傞暔棟検偼偄偔傜偱傕偁傝傑偡丅偲偡傟偽丄
1屄偺CPU偺拞偵丄恾-1偵昤偄偨慡偰偺忬懺傪摨帪偵媗傔崬傓帠傕丄尨棟揑偵偼偱偒傞偼偢偱偡丅
偟偐傕偦傟傜偺忬懺偼丄EPR岠壥偵傛傞挿嫍棧憡娭偵傛偭偰丄弖帪偵捠怣偟傑偡丅
丂偙偆偟偰丄CPU亊1偱丄攝慄晄梫偱忬懺娫偺捠怣懍搙柍尷戝偱丄姰慡偵僔儞僋儘偟偰摦嶌偡傞丄
柌偺挻暲楍僐儞僺儏乕僞乕偺弌棃忋偑傝偱偡丅偟偐傕忬懺偺愝掕傪曄偊偰傗傟偽丄斈梡梡搑偵傕巊偊傑偡丅
栤戣偼丄偦偺傛偆側検巕忬懺傪挿帪娫堐帩偡傞偺偑擄偟偄帠偱偡丅
柧傜偐偵忋婰偺忦審偼丄儅僋儘側検巕僐僸乕儗儞僗偺椺偵側傝傑偡丅
儅僋儘側検巕岠壥傪摼傞偨傔偵偼丄戝偒側僄僱儖僊乕偑昁梫偱偡丅
検巕CPU偑丄旕忢偵尩偟偄暔棟揑忦審傪僋儕傾偟側偗傟偽側傜側偄偺偼丄柧傜偐偲巚偄傑偡丅
偙傟偼堦庬丄忢壏挻揱摫偺尋媶偲帡偰偄傑偡丅挻揱摫偱偼嬌掅壏偺堐帩偑廳梫偱丄
挻揱摫偺婲偙傞椪奅壏搙傪彮偟偱傕忋偘傞偨傔偵丄崅偄壏搙偱傕挻揱摫傪婲偙偟傗偡偄慺嵽傪扵偟偨傝丄
崌惉偟偨傝偟傑偡丅
乽検巕僐儞僺儏乕僞乕乿傪僉乕偵丄Google偟偰傒偰偔偩偝偄丅
偗偭偙偆嶳偺傛偆偵僸僢僩偟傑偡丅
偦偺拞偵偼戝庤揹婥儊乕僇乕偺尋媶強傕偗偭偙偆偁傝傑偡偑乮愭峴搳帒偱偡偹丄偒偭偲乯丄
傗偭偰偄傞帠偼丄偦偺尩偟偄忦審偺堐帩偲丄検巕CPU偵側傝傗偡偄慺嵽扵偟偲偄偭偨妶摦偑栚棫偪傑偡丅
偲偄偆傢偗偱乽検巕僐儞僺儏乕僞偲偼丄嬌掅壏偺傛偆側嬌尷忬懺傪嵽椏偵壽偟丄
偦偺偲偒偵敪婗偝傟傞惗偺暔棟朄懃偺埿椡偵傛偭偰丄挻暲楍壔傪峴偆巇妡偗偩乿偲尵偊傞偲巚偄傑偡丅
嬌尷忬懺傪挿帪娫堐帩偡傞帠偼丄寢嬊偼媄弍揑栤戣偱偡丅媄弍揑栤戣偼丄嬥偲帪娫偝偊偁傟偽昁偢夝寛偱偒傑偡丅1曈46km偺棫曽懱CPU偩偭偰丄塅拡嬻娫偱柍棟偡傟偽100擭屻偵偼偱偒傞偱偟傚偆乮塅拡嬻娫側傜丄曻擬栤戣傕懄帪夝寛偱偡乯丅検巕僐儞僺儏乕僞偑擔忢揑摴嬶偵側傞擔偼丄偦傫側偵墦偔側偄偐傕偟傟傑偣傫丅
NO.1700丂丂柺敀偐偭偨偗偳丄崅偐偭偨杮丂丂丂2007.12.25丂丂丂俢俢俿
杮戙偲庰戙傪巊偄偡偓偰丄壟偝傫偵搟傜傟偨偲偄偆榖偱偡丅
侾丏3儢寧慜
3儢寧慜丄戝妛惗嫤偺杮壆偱暔怓偟偰偨傜丄側傫偲師偺杮偑偨傑偨傑彂扞偵偁傝傑偟偨丅
丂丂丂悢妛偲揘妛偺娫
丂丂丂懞揷慡
丂丂丂嬍愳戝妛弌斉晹丆1998擭戞1嶞乮憹嶞偼丄嫲傜偔側偟乯
丂丂丂18儁乕僕丆7600墌
懞揷慡偺乽悢妛偺揘妛乿偼埲慜偙偙偱傕徯夘偟傑偟偨偑丄媄弍揑偵惍旛偝傟偨嬤戙埲崀偺悢妛偲丄
僊儕僔儍埲棃偺帺慠揘妛偲偺娭學傪丄杮婥偱媍榑偡傞怑嬈悢妛幰偼丄
擔杮偱偼嫲傜偔偙偺恖偩偗偱偼側偄偐偲巚偄傑偡丅撉傫偱傢偐傝傑偟偨偑丄
懞揷慡乮巰傫偱傑偣傫乯偼丄巰嫀偟偨峀廳揙偲傕恊岎偑偁偭偨偺偩偲抦傝傑偟偨丅
峀廳揙偼丄擔杮偺暔棟妛巎尋媶傪悽奅儗儀儖偵墴偟忋偘偨丄嵟弶偺1恖偱偡丅
偱傕抣抜偼丄318儁乕僕偱7600墌乮惻暿乯丒丒丒丅
偱傕丄偙偙偱尒摝偟偨傜丄師偵偍栚偵偐偐傟傞偺偼丄20擭屻偺乽戝妛弌斉晹暅姧僼僃傾乿
偲偐柤柫偭偨婭埳崙壆庡嵜偺揦摢偱偼側偄偩傠偆偐丠丅丒丒丒懄擔峸擖丅
丒丒丒僠乕儞両丆\7,600乮惻暿乯
偲偙傠偑丄偦偺悢擔屻偵丄師偺杮偑婭埳崙壆偵暯愊傒偝傟偰偄偨偺偱偡丅
丂丂丂恄偼栂憐偱偁傞
丂丂丂儕僠儍乕僪丒僪乕僉儞僗
丂丂丂憗愳彂朳丆2007擭5寧弶斉丆摨7寧3斉
恖婥偐傜峫偊偰丄嫲傜偔偙偺杮偼側偔側傝傑偣傫丅巹偼傕偪傠傫柍恄榑幰偱偡偑丄
偦傟偱傕偙偙傑偱偁偐傜偝傑側戣柤偼丄嶐崱捒偟偄偲巚偄傑偟偨丅
壗偐丄傢偗偁傝側偺偱偼丠丅偟偐傕嶌幰偼丄乽棙屓揑側堚揱巕乿
偱桳柤側儕僠儍乕僪丒僪乕僉儞僗偱偼側偄偱偡偐丅偦偟偰懷偵偼丄偙偆彂偐傟偰偄傑偟偨丅
乽偁偺僪乕僉儞僗偑丄側偤偙偙傑偱傓偒偵側傞偺偐丠乿
棙屓揑側堚揱巕 佁 恄偼栂憐 佁 僪乕僉儞僗偑傓偒偵側傞丅
偙偺峔恾偼丄偳偆偵傕枺椡揑偱偟偨丅傓偒偵側偭偨傢偗偼丄彉暥偱偡偖偵傢偐傝傑偡丅
乽巹偼丄僯儏乕儓乕僋偺杅堈僙儞僞乕價儖偵椃媞婡偑撍偭崬傫偩帠審傪抦偭偨帪偵丄
廆嫵偲偦傟傜偵娭傢傞悽奅忣惃偵娭偟偰丄壗傜偐偺帠傪尵傢偞傞摼側偄婥帩偪傪帩偭偨乿
偙偺杮偼斵偺惓捈側婥帩偪偱偁傝丄恑壔惗暔妛幰偲偟偰偺堄尒昞柧偩偲巚偄傑偡丅
壢妛幰偲偟偰偺斵偺巚偄偵懳偟偰丄巹偼僐儊儞僩偟傑偣傫丅撉傫偱傒偰壓偝偄丅
偙偺杮偼偁側偨傪乽傑偭偲偆側柍恄榑幰偵側傞傛偆偵乿丄梡堄廃摓偵978儁乕僕傕偐偗偰愢摼偟偰偔傟傑偡丅
丒丒丒僠乕儞両丆崌傢偣偰\10,100乮惻暿乯
偙偺寧偼庰傕撣傒偡偓偰丄壟偝傫偵偟偙偨傑搟傜傟傑偟偨丒丒丒丅
俀丏2儢寧慜
傑偢抣抜傪偁偘傑偡丅偙偙偑丄摉婰帠偺杮榑偱偡丅
丂丂丂怱偺塭侾
丂丂丂儘僕儍乕丒儁儞儘乕僘
丂丂丂傒偡偢彂朳丆2001擭12寧
丂丂丂248儁乕僕丆3800墌乮惻暿乯
丂丂丂怱偺塭俀
丂丂丂儘僕儍乕丒儁儞儘乕僘
丂丂丂傒偡偢彂朳丆2002擭3寧
丂丂丂278儁乕僕丆3900墌乮惻暿乯
嶌幰儘僕儍乕丒儁儞儘乕僘偼丄儂乕僉儞僌偲偺嫟摨尋媶偱桳柤偱丄
崻偭偙偺晹暘偼乮悽奅桳悢偺乯悢妛幰偱偡偑丄堦棳偺暔棟妛幰偱傕偁傝傑偡丅
偙偺杮偺庯巪偼丄乽儁儞儘乕僘丄怱偺撲偵挧傓両乿偱偡丅
偟偐偟526儁乕僕偱7700墌乮惻暿乯丒丒丒崅偡偓傞偧偙傝傖丒丒丒偱傕愭寧丄
318儁乕僕偱7600墌乮惻暿乯傪攦偭偨偠傖側偄偐丠丒丒丒
偟偐傕乽怱偺塭乿偺慜恎偱偁傞乽峜掗偺怴偟偄怱乿偼丄堦弖偱杮壆偐傜徚偊偨丒丒丒偳偆偡傞丠
丒丒丒撪梕偼偙偆偱偡丅
儁儞儘乕僘偼彉暥偱丄偙偆尵偄傑偡丅
乽戞1晹偱偼丄乽棟夝乿偲偄偆恖娫偺堄幆偼丄
扨側傞寁嶼偵偼側偟偊側偄偙偲傪峴偭偰偄傞偺偩偲偡傞巹偺僥乕僛傪嫮偔巟偊傞丄
揙掙揑偐偮徻嵶側媍榑傪採嫙偡傞乿
偄傗偭丄椡嫮偄偱偡傛偹丅傢偔傢偔偟傑偟偣傫偐丠丅
斵偼嵟弶偵堄幆傪傔偖傞懺搙偲偟偰丄師偺3偮傪偁偘傑偡丅
- 恖娫偺擼偼乮堄幆偼乯丄尰峴偺斈梡僐儞僺儏乕僞偑丄嫲傠偟偔暋嶨偵側偭偨傕偺偵夁偓側偄丅廬偭偰丄 僯儏乕儔儖僱僢僩儚乕僋側偳傪捛媮偟偰偄偗偽丄偄偮偐偼丄恖擼傪嵞尰偱偒傞丅
- 恖擼乮偲堄幆乯偼丄寁嶼晄壜擻惈偵崻嫆傪帩偮丅廬偭偰丄尰峴偺斈梡僐儞僺儏乕僞偼堄幆傪帩偮偼偢偑側偄丅
- 恖偺堄幆乮嵃乯偼丄暔棟揑側傕偺偱偼側偄丅廬偭偰尰峴偺壢妛偱偼丄堄幆乮恖擼乯傪夝柧偱偒傞偼偢偑側偄丅
埲忋偼柧傜偐偵僗僥儗僆僞僀僾偱偡偑丄懨摉側傕偺偲巚偊傑偡丅
儁儞儘乕僘帺恎偼丄(2)傪巟帩偟偰偄傑偡丅偙偙偱愢柧偟側偗傟偽側傜側偄偺偼丄
寁嶼晄壜擻惈偵崻嫆傪帩偮丄偲偄偆帠偱偡丅
寁嶼晄壜擻惈偲偼丄旕悢妛揑偲偐壢妛偺揔梡斖埻奜偲偐偄偆堄枴偱偼偁傝傑偣傫丅
偦傟偱偼(3)偲戝嵎側偄偱偡丅斵偑尵偆寁嶼晄壜擻惈偲偼丄
乽堦掕栤戣椞堟偑梌偊傜傟偨偲偒丄偦偺椞堟撪偵娷傑傟傞擟堄偺栤戣慡偰偵丄
晛曊揑偵揔梡壜擻側寁嶼庤弴乮斈梡傾儖僑儕僘儉乯偑懚嵼偟側偄帠乿
偱偡丅偦偆偱偡丄儁儞儘乕僘偼乽僎乕僨儖偺晄姰慡惈掕棟乿偺帠傪尵偭偰偄傑偡丅
偙傟偼屄暿偺栤戣偵懳偟偝偊丄姰慡偵悢妛揑偱懨摉側夝朄偼懚嵼偟側偄丄
偲尵偭偰偄傞傢偗偱偼偁傝傑偣傫丅偨偩慡偰偺栤戣偵揔梡偟偆傞斈梡傾儖僑儕僘儉偼側偄丄
偲尵偭偰偄傞偩偗偱偡丅偁傞偲偡傞偲丄偦偺棟榑偼柕弬偡傞偐傜偱偡丅
尵傢傟偰傒傟偽妋偐偵偦偆偱丄1)偺棫応偼丄僠儏乕儕儞僌儅僔儞偱偁傞尰峴偺PC乮斈梡僐儞僺儏乕僞乯偺尷奅傪堦曕傕弌側偄傕偺偱偡丅尰峴偺僾儘僌儔儈儞僌偼乮怑嬈側偺偱椙偔傢偐傝傑偡偑乯丄斈梡傾儖僑儕僘儉偺懚嵼傪慜採偵偟傑偡丅偦偺壖掕側偟偱偼丄僾儘僌儔儉偡傞婥偡傜婲偒傑偣傫乮寢壥偑曐徹偝傟側偄偺偱乯丅偟偐偟乽僎乕僨儖偺晄姰慡惈掕棟乿偼乽僠儏乕儕儞僌偺寛掕晄壜擻掕棟乿偲摨偠偱偡丅尰峴偺斈梡僐儞僺儏乕僞偺栤戣夝寛擻椡偵偼丄尨棟揑偵柧傜偐側尷奅偑偁傞偺偱偡丅
偵傕娭傢傜偢(1)偺棫応偼丄偙偲偑堄幆偺僔儈儏儗乕僔儑儞偱偁傞偲偄偆偺偵丄
偦偺尷奅偲偼柍娭學偵傗傟傞偲嵟弶偐傜寛傔偰偐偐偭偰偄傞丄偲儁儞儘乕僘偼斸敾偟傑偡丅
斵偑偁偘傞椺偼偙偆偱偡丅恖娫偑偁傞悢妛棟榑傪偮偔傞帪偵偼丄
偦偺棟榑傛傝傕柧傜偐偵峀偄撪梕傪娷傓丄儊僞棟榑偺拞偱巚峫偡傞丅
儊僞棟榑偵娷傑傟傞丄栚昗棟榑帺懱偑偡偱偵晄姰慡惈傪帩偭偰偄傞偺偩偐傜丄
儊僞棟榑傕摉慠晄姰慡惈傪帩偮丅偵傕偐偐傢傜偢惓偟偄棟榑傪偮偔傞帠偑偱偒傞丅
偦傟偼偳偆偟偰偐丠丅傑偢斈梡傾儖僑儕僘儉偩偗傪梡偄偰丄
慡晹偺帠傪傗偭偨偺偱偼側偄偺偼柧傜偐乮偦傟偼晄壜擻乯丅偩偲偡傟偽丄
a) 恖娫偼帺恎偺傾儖僑儕僘儉偺晄旛傪堄幆偟偮偮丄
宱尡傗悢抣幚尡傪捠偟偰晄旛傪曗偄丄惓偟偄悢妛棟榑傪偮偔傞偺偐丠丏
b) 恖娫偼丄斈梡傾儖僑儕僘儉偺尷奅傪挻偊偰丄寁嶼晄壜擻側宯傪
乽棟夝偡傞乿擻椡傪帩偪丄姰慡偵惓偟偄偲偄偆妋怣偺傕偲丄惓偟偄悢妛棟榑傪偮偔傞偺偐丠丏
偲側傞偩傠偆偲丅
儁儞儘乕僘偺棫榑偼偄偐偵傕掕惈揑偱丄尰帪揰偱偼幚徹偱偒傞椶偺傕偺偱偼偁傝傑偣傫丅
屄恖揑偵偼a)傪嵦梡偟偰偄偨偺偱偡偑乮偮傑傝丄寛傔偰偐偐偭偰偄偨傢偗偱偡偑乯丄
儁儞儘乕僘偼b)埲奜怣偠傜傟側偄偲尵偄傑偡丅偙傟偼悢妛幰偱偁傞斵偺丄婾傜偞傞婥帩偪偩傠偆偲巚偄傑偡丅
偦偟偰b)偩偲偡傞偲丄妋偐偵偁傞壜擻惈偑戱偗傑偡丅
偦偆偟偰丄偦偺壜擻惈偺崻嫆傪暔棟揑偵扵媮偡傞偨傔偵丄戞2晹偑巒傑傝傑偡丅
偪側傒偵戞1晹偱偼丄埲忋偺傛偆側榖乮埲忋偼丄巹側傝偺傑偲傔偱偡乯傪偡傞偨傔偵丄
僎乕僨儖偺晄姰慡惈掕棟偲僠儏乕儕儞僌偺寛掕晄壜擻掕棟偵娭偟偰丄
僠儍乕僠偺兩寁嶼傑偱娷傔偰丄揙掙揑偐偮徻嵶側媍榑偑採嫙偝傟傑偡
乮揙掙揑偡偓偰丄敿暘傕棟夝偱偒傟偽偄偄傎偆偩丄偲偄偆偺偑屄恖揑側姶憐偱偡偑乯丅
戞2晹偱偼嵟弶偵丄検巕椡妛偺榑棟峔憿偑奣娤偝傟傑偡丅偦偺拞偱僉乕偵側傞偺偼丄
攇摦曽掱幃偺寛掕榑揑懁柺乮倀夁掱乯偲丄倀夁掱偺寢壥偺揔梡偵娭偡傞旕寛掕榑揑懁柺乮俼夁掱乯偱偡丅
検巕椡妛偺婎慴曽掱幃僔儏儗乕僨傿儞僈乕偺攇摦曽掱幃偼丄検巕忬懺傪昞偡僸儖儀儖僩嬻娫偵嶌梡偡傞丄
儐僯僞儕乮Unitary乯嶌梡慺偲傒側偣傞偺偱丄攇摦曽掱幃偺夝偱偁傞攇摦娭悢傪倀夁掱偲屇傃傑偡丅
倀夁掱偺寁嶼偼丄僯儏乕僩儞偺塣摦曽掱幃偲摨偠偔丄弶婜忬懺偵傛偭偰寛傑傞姰慡側寛掕榑揑帪娫敪揥偱偡丅偄偭傐偆攇摦娭悢偐傜棻巕偺埵抲傪寛掕偡傞嵺側偳偵偼丄攇懇偺廂弅乮Reduction乯偲屇偽傟傞憖嶌偑巊傢傟傑偡丅偦傟偱俼夁掱偱偡丅俼夁掱偼傕偪傠傫柧妋側婯懃偱弌棃偰偄偰丄偁傜備傞応柺偵揔梡壜擻偱偁傝丄尰幚揑側巊梡偵偍偄偰偺晄旛偼偁傝傑偣傫丅偟偐偟俼夁掱偼丄僔儏儗乕僨傿儞僈乕曽掱幃偐傜摫偐傟傞帠偺側偄宱尡懃偱偡丅偦偟偰俼夁掱偵偍偄偰丄検巕椡妛偵摿桳側妋棪惈傗EPR岠壥乮検巕岠壥乯偑尰傟傑偡丅
儁儞儘乕僘偺堄尒偱偼丄検巕椡妛偼俼夁掱傪傑偲傕偵愢柧偱偒側偄偺偱丄
偦傟偼晄姰慡偩偲側傝傑偡丅傾僀儞僔儏僞僀儞傕EPR榑暥偱摨偠庯巪偺敪尵傪偟傑偟偨偑丄
夝寛偺弍偑側偐偭偨偺偱丄帪戙偺悥惃偼僐儁儞僴乕僎儞夝庍偵孹偒傑偟偨丅
偟偐偟偦傠偦傠EPR榑暥偐傜80擭偱偡丅
偦偺娫杮摉偼丄娤應栤戣偺媍榑偺愨偊偨帠偼偁傝傑偣傫偱偟偨丅
傒傫側杮摉偼僐儁儞僴乕僎儞夝庍偵晄枮偩偭偨偟丄
検巕椡妛偼偳偙偐晄姰慡偩偲姶偠偰偄偨偺偩偲巚偄傑偡丅
EPR榑暥偐傜80擭屻丄儁儞儘乕僘偼丄傕偭偲尰戙揑側俼夁掱偺夝寛傪栚巜偟傑偡丅
埲壓偼丄偲偁傞彂昡偐傜偺庴偗攧傝偱偡丅
乽検巕榑偲堦斒憡懳惈棟榑偺摑堦傪峴偍偆偲偡傞嵺丄
懡偔偺暔棟妛幰偼丄検巕榑偵崌傢偣偰堦斒憡懳惈棟榑傪廋惓偟傛偆偲偟偰偄傞丅
偟偐偟儁儞儘乕僘偼媡傪栚巜偡乿
偪傚偭偲尵偄偡偓偐側偲傕巚偄傑偡偑丄偙偺彂昡偼丄儁儞儘乕僘偺堄恾偵婥偯偐偣偰偔傟傑偟偨丅
検巕榑偲堦斒憡懳惈棟榑偺摑堦偲偼丄師偺傛偆側帠偱偡丅
検巕椡妛偺婎慴曽掱幃偐傜俼夁掱傪愢柧偱偒側偄偲偄偆帠偲偼暿偵丄椉棟榑偵懳偟偰偼丄
偦傟傜偑採彞偝傟偨20悽婭弶摍偐傜偺寽埬帠崁偑偁傝傑偟偨丅傑偢僯儏乕僩儞椡妛偱偡偑丄
偦傟偼検巕岠壥傕憡懳榑揑岠壥傕娷傑側偄偲偄偆堄枴偱屆揟棟榑偲屇偽傟傑偡丅
堦曽丄憡懳榑偼傕偪傠傫憡懳榑揑岠壥傪娷傒傑偡偑丄検巕岠壥傪娷傑側偄偲偄偆堄枴偱屆揟揑偱偡丅
偲偙傠偑検巕榑傕乮僆儕僕僫儖側宍偱偼乯丄憡懳榑揑岠壥傪娷傑側偄偺偱丄屆揟榑偲偄偆帠偵側傝傑偡丅
傛偭偰丄検巕榑偲堦斒憡懳惈棟榑傪摑堦偟偨壗偐偑丄傛傝姰慡側棟榑偱偁傞偙偲偼丄
傕偆70擭埲忋慜偐傜柧傜偐偩偭偨偺偱偡丅偟偐偟丄偄傑偩偵夝寛偟偰偄傑偣傫丅
儁儞儘乕僘偺堄恾偼丄検巕榑傕堦斒憡懳惈棟榑傕懨摉偵廋惓偡傞偙偲偱偡丅
検巕榑偲憡懳榑偺摑堦偑崲擄偩偭偨偺偼丄憡懳榑偑旕慄宍偱検巕榑揑側慄宍偺掕幃壔傪庴偗偮偗側偄偲偐丄
堦斒憡懳惈尨棟偑梋傝偵尩偟偄梫媮偱丄暯扲側帪嬻傪慜採偲偟偨検巕榑偑偦傟傪庴偗偮偗側偄偲偐丄
怓乆偁偭偨偺偱偡偑丄怓乆傪傑偲傔傞偲丄椉棟榑偑敪尰偡傞僗働乕儖偑堘偄偡偓傞偲偄偆帠偵傕側傝傑偡丅
僩儞僱儖岠壥傗晄妋掕惈尨棟偲偄偭偨検巕岠壥偑尠挊側偺偼丄奣偹尨巕儗儀儖埲壓偺儈僋儘側椞堟偱偡丅
側偺偱検巕岠壥偑擔忢儗儀儖偵尰傟傞帠偼傑偢偁傝傑偣傫乮棙梡偼偱偒傑偡偑乯丅
憡懳榑岠壥偑尠挊偵側傞偺偼丄價僢僋僶儞偲偐嬧壨廤抍偲偄偭偨塅拡榑儗儀儖偱偺榖偵側傝傑偡丅
儁儞儘乕僘偼俼夁掱傪丄廳椡岠壥乮憡懳榑揑岠壥乯偵廬偭偰丄帪嬻峔憿偑慖偽傟傞夁掱偩偲採埬偟傑偡
乮仼 嬶懱揑側巇妡偼丄巹偵偼棟夝晄壜擻偱偡乯丅斵偼偦傟傪媞娤揑廂弅夁掱
乮Objective Reduction丆OR夁掱乯偲屇傃傑偡丅偦偟偰OR夁掱偑敪惗偡傞僗働乕儖僆乕僟乕傪丄
奣嶼偟偰傑偱傒偣傑偡丅偦偺僗働乕儖僆乕僟乕偼丄斵偵傛傟偽丄扨嵶朎惉暘偱偁傞僝僂儕儉僔偺懱挿傛傝
彮乆彫偝偄掱搙偲偄偆丄廬棃偺検巕榑偵偲偭偰偼丄搑換傕側偔嫄戝側僗働乕儖偱偡丅
傛偭偰惗暔偼丄偦偺嵶朎偺拞偱丄摿偵擼偺恄宱嵶朎偼丄OR夁掱偲偄偆検巕夁掱傪丄
椺偊偽EPR岠壥偲偄偆宍偱棙梡偟偰偄傞壜擻惈傕偁傞帠偵側傝傑偡丅偙偙傑偱棃傟偽丄
儁儞儘乕僘偺峴偒愭偼傕偆尒偊偰偒傑偡丅斵偼丄擼偼検巕僐儞僺儏乕僞偱偼側偄偺偐丠丄偲尵偄偨偄偺偱偡丅
偨偩偟嵟屻偵丄戝媡揮儂乕儉儔儞偑懸偭偰偄傑偡丅
懕偔復偱偼丄廬棃峫偊傜傟偰偄偨傛傝傕儅僋儘側僗働乕儖偱丄
嵶朎偑擔忢儗儀儖偱検巕岠壥傪棙梡偟偰偄傞偐傕偟傟側偄偲偄偆丄
惗暔妛揑側偄偔偮偐偺椺徹偑帵偝傟傑偡丅椺偊偽恄宱宯偺懚嵼偟側偄扨嵶朎惗暔傗僶僋僥儕傾偵偝偊丄
怘暔憱壔惈偲偐岝憱壔惈偲偐偄傢傟傞丄乽峫偊偰峴摦偟偰偄傞乿偐偺傛偆偵傒偊傞廗惈偑懚嵼偟傑偡丅
偦偺婡峔偺拞怱乮旝彫娗乯傪挷傋偰傒傞偲丄偁偨偐傕惗懱桳尷僆乕僩儅僩儞偵傛偆偵側偭偰偄傞壜擻惈偑偁傝丄
偟偐傕偦偺戝偒偝偼丄OR夁掱偺敪惗僗働乕儖偵傆偝傢偟傕偺偩偲儁儞儘乕僘偼尵偄傑偡丅
報徾偵巆偭偨朤徹偺堦偮偼丄旝彫娗偼僝僂儕儉僔偵傕恖娫偺擼嵶朎偵傕懚嵼偟丄
杻悓偼擼嵶朎偺旝彫娗偺摥偒傪慾奞偟偰丄恖傪婥愨偝偣傞帠偑傢偐偭偰偄傞偑丄
摨條偵僝僂儕儉僔傕杻悓偵偐偐傞丄偲偄偆傕偺偱偟偨丅
偙偙傑偱傑偲傔傞偲丄検巕岠壥偼廬棃峫偊傜傟偰偄偨傛傝傕儅僋儘側僗働乕儖偱丄
擔忢揑偵敪尰偟丄偦傟傪擼嵶朎偼擔忢揑偵棙梡偡傞検巕僐儞僺儏乕僞偐傕偟傟側偄丄
偲偄偆帠偵側傝傑偡丅偟偐偟偦傟偑b)偱弎傋偨丄寁嶼晄壜擻側宯傪乽棟夝偡傞乿擻椡偲丄
偳偆偮側偑傞偺偱偟傚偆丠丅儁儞儘乕僘偼丄尰峴偺堦斒憡懳惈棟榑偺尋媶偺拞偵丄
偦偺椺徹偑偁傞偲尵偄傑偡乮傆偮偆偺恖偼丄偙傫側帠偼峫偊傑偣傫傛偹丒丒丒乯丅
c) 堦斒憡懳榑傪尋媶偟偰偄傞偲丄廳椡偑掕傔傞帪嬻偺4師尦婔壗妛偺乽宆乿
傪敾掕偡傞昁梫偵敆傜傟傞偑丄宆敾掕栤戣偼丄寁嶼晄壜擻偱偁傞帠傪徹柧偱偒傞
乮斈梡傾儖僑儕僘儉偼懚嵼偟側偄丒丒丒偩偐傜丠乯丅
d) 忋婰敾掕栤戣偵堦斒寛掕庤懕偒偼側偄偺偩偑丄OR夁掱偑杮摉偵懚嵼偡傟偽丄
偦傟偵傕娭傢傜偢検巕椡妛偼丄宆偺堦偮傪乮惓偟偔丠乯
帺慠偵慖傇帠偵側傞丅壗偑惓偟偄偐偺敾掕婎弨偼晄柧偩偑丅
e) 傛偭偰擼嵶朎偑OR夁掱傪杮摉偵棙梡偟偰偄傞偺偱偁傟偽丄
偦傟偵敽偆慖戰岠壥偵傛偭偰丄恖娫偼寁嶼晄壜擻惈偺尷奅傪撍攋偱偒傞偐傕偟傟側偄丅
杮摉偐乣乣偭両両両丄偭偰嫨傃偨偔側傞婥帩偪偼傢偐傝傑偡丅
偱傕偄傑儁儞儘乕僘偼丄戝媡揮儂乕儉儔儞傪曻偭偨傫偱偡傛丅偦傟偼丄
乽尰峴偺検巕僐儞僺儏乕僞傕丄寢嬊偼僠儏乕儕儞僌儅僔儞偵偡偓側偄丅
尰峴偺検巕僐儞僺儏乕僞偼挻暲楍壔偝傟偨僲僀儅儞宆僐儞僺儏乕僞偲寁嶼榑揑偵偼摨偠偱偁傝丄
寁嶼晄壜擻惈偺尷奅撪偵偁傞乿
偲偄偆堦暥偐傜傢偐傝傑偡丅偙偺堦暥偼丄梋傝偵傕偁偭偝傝偲彂偐傟偰偄傞偨傔偵丄
尒偨尷傝偺彂昡偱偼扤傕拲栚偟偰偄側偐偭偨偺偱偡偑丄
乽恖娫偺堄幆偼丄尰峴偺検巕僐儞僺儏乕僞偝偊椊夗偡傞丄検巕夁掱傪棙梡偟偨壗偐偱偁傞乿偲丄
儁儞儘乕僘偼尵偭偰偄傞偺偱偡丅
乽怱偺塭乿偼埲忋偱廔傢傝偱偡偑丄斵偺尵偭偰偄傞帠偼丄
偦偺嬝偱丄堦斒揑偵庴偗擖傟傜傟偰偄傞傢偗偱偼偁傝傑偣傫丅
斵偺棫榑偼丄尰忬偱偼嫲傜偔僋儗僀僕乕側晹椶偵擖傝傑偡丅
偟偐偟丄傒偡偢彂朳偑儁儞儘乕僘偺柤慜偵閤偝傟偰娫堘偭偰弌偟偰偟傑偭偨
乽僩儞僨儌杮乿偱偼偁傝傑偣傫丅斵偺偁偘偨乽忬嫷徹嫆乿傪慡偰暲傋偰丄
傕偆堦搙慡懱傪挱傔偰傒偰壓偝偄丅彮側偔偲傕丄
丂丂丂丒昗弨棟榑偵懃偭偰偄傞丅
丂丂丂丒弎傋傜傟偨斖埻偱丄撪晹柕弬偼側偄丅
丂丂丂丒奺崁栚偵偮偄偰丄偦傟偧傟尰幚偺忬嫷徹嫆偑偁傞丅
偲巚偊傑偡乮僩儞僨儌杮敾掕偺斈梡傾儖僑儕僘儉丠乯丅
儁儞儘乕僘偼丄掕惈揑尨棟揑偵丄壗偑壜擻偱偁傞偐偺丄偦偺尷奅傪扵偭偰偄傞偺偱偡丅
偦偺寢榑偺堦偮偑乽恖娫偺堄幆偼丄検巕僐儞僺儏乕僞埲忋偺傕偺偱偁傞乿偱偟偨丅偙傫側椺偑偁傝傑偡丅
戝棨堏摦愢乮僾儗乕僩僥僋僩僯僋僗乯偼丄巹偑彫妛惗偺崰偼僋儗僀僕乕側柌暔岅偱偟偨丅
偦傟偑拞妛峑枛偺棟壢偺嫵壢彂偁偨傝偐傜暤埻婥偑曄傢傝巒傔丄崅峑偺崰偵偼妛夛偱傕擣抦偝傟偰丄
乽偝傛偆側傜偲尵傢側偄偱丒丒丒岝偲塭偺傛偆偵丒丒丒乿偲屲栘傂傠偟偑庡戣壧傪鎼偄偁偘偨丄
弶戙乽捑杤乿偑弌棃忋偑傝傑偡丅偮偄偙偺娫丄憪撱孨庡墘偱儕儊僀僋偝傟丄
乽擔杮埲奜慡晹捑杤乿偲偄偆僷儘僨傿乕塮夋傑偱弌傞巒枛丒丒丒丅
乽怱偺塭乿偼丄摉戙悘堦偺悢妛幰丒暔棟妛幰偱偁傞挊幰偑丄憐憸椡傪巚偄偭偒傝奼偘偰丄
杮婥偱挧傫偩帋榑偱偡丅僋儗僀僕乕丒儁儞儘乕僘偑丄愭嬱偗偺儁儞儘乕僘偵側傜側偄
擔偑棃側偄偲偼尷傝傑偣傫丅
丒丒丒僠乕儞両丆崌傢偣偰\7,700乮惻暿乯
慜偺寧偺帠偑偁偭偨偺偱丄壟偝傫偼敿暘妏傪弌偟偰傑偟偨丒丒丒丅
俁丏愭寧
偙偆偄偆偺傪僔儞僋儘僯僔僥傿乕偲偄偆偺偱偟傚偆偐丠丅
巹偼尰嵼戝妛偱乽寁嶼悢妛乿偺島媊傪庴偗偰偍傝丄偦偙偱偼寁嶼壜擻惈偑惉傝棫偮斖埻偱丄
桳尷僆乕僩儅僩儞側偳偑掕媊偝傟傑偡丅嶐擔丄
寛掕惈桳尷僆乕僩儅僩儞偲丄旕寛掕惈桳尷僆乕僩儅僩儞偺庴棟尵岅偺摍壙惈傪丄
傗偭偲帺椡偱徹柧偟傑偟偨乮偲巚偭偰傞偩偗偐傕偟傟傑偣傫偑丒丒丒乯丅
屻偼兠摦嶌晅旕寛掕惈桳尷僆乕僩儅僩儞偲丄惓懃尵岅偺榖偐丒丒丒丅
偱傕偙偆偄偆榖偼丄偡偛偄恏婥廘偄偲偄偆偺偑丄尰幚偺巹偺報徾偱偡丅
偱傕兠摦嶌晅旕寛掕惈桳尷僆乕僩儅僩儞偭偰丄僀儀儞僩傪帩偮Windows System偲摨偠偱偼丠偭偰丄
偪傚偭偲巚偄傑偟偨丅偦傟偼偦傟偲偟偰丒丒丒丅
嬛梸偟傛偆偲巚偭偨傫偱偡偑丄
丂丂丂壢妛偲忣曬棟榑
丂丂丂L.僽儕儖傾儞
丂丂丂傒偡偢彂朳丆1969擭戞1嶞丆2002擭戞6嶞
丂丂丂354儁乕僕丆6900墌乮惻暿乯
側傫偰杮偑偁偭偨偺偱偡丅偙傟偼柤挊偱偡丅
椺偊偽埵憡揑僄儞僩儘僺乕偲應搙榑揑僄儞僩儘僺乕傪丄朻摢偺偨偭偨19儁乕僕偱丄
偁偭偝傝偲柧夣偵掕媊偟偰偔傟傑偡丅巹偑偦傟傜偺掕媊偵嵟弶偵弌夛偭偨偺偼丄
僂傿乕僫乕偺僒僀僶僱僥傿僋僗乮偙傟傕柤挊偱偡乯偵徯夘偝傟偰偄偨僔儍僲儞偺捠怣棟榑偵偍偄偰偱偟偨丅
偲傫偱傕側偔擄偟偄忋偵丄挿偐偭偨丅偟偐傕棟夝偱偒側偐偭偨丅
栿幰屻彂偒偵傛傞偲丄尨挊幰偺僽儕儖傾儞偼1889擭惗傑傟丄偙偺杮偺戞1嶞偑弌偨帪偵偼丄
偡偱偵80嵨偱偟偨丅僽儕儖傾儞偼丄尰戙偺幚徹庡媊偱偁傞憖嶌庡媊傪嫮椡偵採彞偟偨恖偱傕偁傝丄
検巕椡妛偺娤應栤戣偵偼昁偢弌偰偒傑偡丅側偺偱斵偑丄忣曬棟榑偺杮傪彂偄偰偄偨偲偟偰傕丄
壗偺晄巚媍傕側偄偺偱偡丅栿幰偵傛傟偽丄忣曬検傪掕媊偡傞戞1晹偲丄
偦傟傪摑寁椡妛揑偵僄儞僩儘僺乕偲娭楢晅偗傞戞2晹偼丄忣曬壢妛偑敪懌偟偰廫悢擭偨偭偨尰嵼偵偍偄偰傕丄
弶妛幰偵偲偭偰偒傢傔偰孾栔揑偱偁傝乮戝巀惉両乯丄屆揟揑婸偒傪幐偭偰偄側偄偲偁傝傑偡丅
偦傟偐傜40擭宱偭偨尰嵼偵偄偨偭偰傕丄偦偺偲偍傝偩偲巚偄傑偡丅
偙偺杮偼撉傒偐偗偱偡偑丄備偭偔傝偲撉傒偨偔側傞旕忢偵旤枴偟偄杮偱偡丅
偨傇傫攧傟側偄偵傕娭傢傜偢丄偙偺傛偆側杮傪掕婜揑偵憹嶞偟偰壓偝傞丄
傒偡偢彂朳條丄偁傝偑偲偆偛偞偄傑偡丅
丒丒丒僠乕儞両丆\6,900乮惻暿乯
偙偺寧偼丄晐偔偰壟偝傫偺婄傪尒傟傑偣傫偱偟偨丒丒丒丅
係丏崱寧
愭擔丄乽寁嶼悢妛乿偺島媊偱儗億乕僩傪弌戣偝傟偰丄
偲偆偲偆巜掕僥僉僗僩傪攦傢偞傞摼側偔側傝傑偟偨丅
丂丂丂僆乕僩儅僩儞 尵岅棟榑 寁嶼榑嘥丆嘦
丂丂丂J.儂僢僾僋儘僼僩丆R.儌僩儚僯丆J.僂儖儅儞
丂丂丂僒僀僄儞僗幮丆1984擭戞1嶞丆2007擭戞27嶞
丂丂丂337亄240亖577儁乕僕丆2800亄2600亖5400墌乮惻暿乯
暿偵柺敀偐偀乣側偄傛丅偟偐傕27嶞傕偟偰傞偔偣偵丄
壗側偺偙偺抣抜丠丅朶棙偩両乮塕偱偡丅埨偄偱偡乯丅
崱寧偙偦偼嬛梸偟傛偆偲巚偄傑偟偨丅偱傕丒丒丒丅偙傟偼傕偆愨懳偵僔儞僋儘僯僔僥傿乕偱偡丅
丂丂丂僐儞僺儏乕僞僾儘僌儔儈儞僌偺奣擮丒媄朄丒儌僨儖
丂丂丂僺乕僞乕丒償傽儞丒儘僀丆僙僀僼丒僴儕僨傿
丂丂丂隳塲幮丆2007擭11寧
丂丂丂906儁乕僕丆8200墌乮惻暿乯
偙偺杮偼傑偩彉暥偟偐撉傫偱偄傑偣傫偑丄撪梕偺庯巪偼傢偐傝傑偡乮偄偪偍偆僾儘側偺偱乯丅
摨彂偼丄擔杮偱巒傔偰弌偨丄杮奿揑側僾儘僌儔儈儞僌妛偺惉彂偲峫偊傜傟傑偡丅
幚嵺丄摨彂偼傾儊儕僇偺偄偔偮偐偺戝妛乮MIT傕娷傑傟傑偡乯
偺忣曬島嵗偱島媊偝傟偨僥僉僗僩偺廤戝惉偱偁傝丄偦偺偨傔偵偙傫側偵暘岤偔側偭偰偄傑偡丅
廬棃偺傛偆偵丄Java傗俠傪廗摼偝偣丄椺戣傪斀暅楙廗偡傞僗僞僀儖偱偼偁傝傑偣傫丅
傑偨丄傾儖僑儕僘儉偩偗偵徟揰傪摉偰偰傕偄傑偣傫丅
拪徾壔偝傟偨僾儘僌儔儈儞僌峴堊偦偺傕偺傪妛偽偣傞杮偱偡丅
僾儘僌儔儉奐敪偵娭傢傞慡偰偺媄弍幰丄嫵堢幰丄棟榑壠偺昁実偺彂偲丄
偄偮偐尵傢傟傞帪偑棃傞偲巚偭偰攦偄傑偟偨丅偩偭偰丄偡偖側偔側傝偦偆側傫偩傕偺丒丒丒丅
丒丒丒僠乕儞両丆崌傢偣偰\13,600乮惻暿乯
庰傕偁偄偐傢傜偢撣傫偱傑偡丅寧枛偑嫲偄丒丒丒丅
俆丏嶨姶
偛懚抦偱偟傚偆偐丠丅偳傫側偵儅僯傾僢僋側愱栧椞堟偱偁偭偰傕丄曣崙岅偱島媊偡傞偺偑昗弨偵側偭偰偄傞旕塸岅寳偺崙偼丄擔杮偔傜偄偟偐側偄偭偰帠傪丅偙傟偼峕屗帪戙傗柧帯埲棃偺揱摑偱偁傝丄愭恖払偺搘椡偺寢徎偱偡丅偨偲偊偳傫側偵擄夝側嵟怴偺悢妛傗暔棟偺彂愋偱偁偭偰傕丄敿擭乣1擭屻偵偼彮側偔偲傕堦夞偼丄偦偺慡栿偑巗堜偺杮壆偵弌夞傝傑偡丅奜崙岅壒抯偱偁傞巹偼丄偙偺娐嫬偵旕忢偵姶幱偟偰偄傑偡丅偄傑偡偑丄偦偺偨傔偵丄擔杮偺堦斒揑側尋媶幰偺塸岅儗儀儖偼丄旕塸岅寳偺崙偺拞偱嵟掅偩偦偆偱偡丅
NO.1699丂丂晄掕曽掱幃俁倶亅俀倷亖侾丂丂2007.12.17丂丂K.F.
晄掕曽掱幃俁倶亅俀倷亖侾偺侾偱側偄帺慠悢夝偑丄乮倶丄倷乯亖乮俀丆俁乯偵尷傜傟傞偙偲傪
徹柧偟傑偡丅
x=2偺偲偒偼丄y=3偲側傞丅
x=3偺偲偒偼丄2y=26偲側傞偐傜丄y偼帺慠悢夝偵側傝偊側偄丅
y=2偺偲偒偼丄3x=5偲側傞偐傜丄x偼帺慠悢夝偵側傝偊側偄丅
偦偙偱丄x亜3丄y亜3側傞帺慠悢夝偑懚嵼偡傞偲壖掕偡傞丅
偙偺偲偒丄3x-1=2y丂偺椉曈傪丄3-1=2偱妱傞偲丄
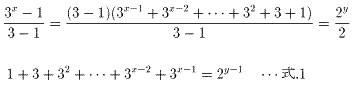
偑摼傜傟傞丅幃.1偺塃曈偼嬼悢偱丄嵍曈偺奺崁偼偡傋偰婏悢偩偐傜丄嵍曈偺崁悢x偼嬼悢偵側傞丅
乮(婏悢亄婏悢)亄(婏悢亄婏悢)亄丒丒丒亄(婏悢亄婏悢)亖嬼悢乯
偦偙偱丄幃.1偺嵍曈傪俀偮偢偮侾慻偵偟偰場悢暘夝偡傞偲丄
丂丂(1+3)(1+32+34+丒丒丒+3x-2)=2y-1丂丂丒丒丒幃.2
偑摼傜傟傞丅幃.2偺椉曈傪4偱妱傞偲丄
丂丂1+32+34+36+丒丒丒+3x-2=2y-3丂丂丒丒丒幃.3
偑摼傜傟傞丅幃.3偱偼丄幃.1偺偲偒偲摨條偵塃曈偑嬼悢側偺偱丄嵍曈偺崁悢丂x/2偼嬼悢偵側傞丅偦偙偱丄幃.3偺嵍曈傪
俀偮偢偮侾慻偵偟偰場悢暘夝偡傞偲丄
丂丂(1+32)(1+34+38+丒丒丒+3x-4)=2y-3丂丂丒丒丒幃.4
偑摼傜傟傞丅偟偐偟丄幃.4偺嵍曈偼丄5傪慺場悢偵傕偮偺偱丄偙傟偼晄崌棟偱偁傞丅
偟偨偑偭偰丄丄x亜3丄y亜3側傞帺慠悢夝偼懚嵼偟側偄丅
屘偵丄3x-2y=1丂偺1偱側偄帺慠悢夝偼丄(x,y)=(2,3)偵尷傜傟傞丅
(徹柧廔傢傝)
NO.1698丂丂嶼妟in媨忛丂丂2007.12.17丂丂悈偺棳傟
戞俀侽侾夞悢妛揑側墳曞栤戣
奆偝傫丄乽擔杮偺婔壗丂壗戣夝偗傑偡偐丠乿乮怷杒弌斉乯乽怺愳塸弐丂僟儞丒儁僪乕嫟挊乿
偲尵偆杮傪偛懚抦偱偡偐丅偦偺拞偵媨忛導搷惗孲搷惗挰擔崅尒恄幮偵戝惓俀擭乮1913擭乯偵
宖妟偝傟偨栤戣傪嶲峫偵偟偰嶌傝傑偟偨丅偟偐偟丄杮偵偼摎偊偵帄傞夁掱偑彂偄偰偁傝傑偣傫丅
偦偙偱丄奆偝傫偺椡傪昁梫偲側傝傑偟偨丅峫偊偰偔偩偝偄丅
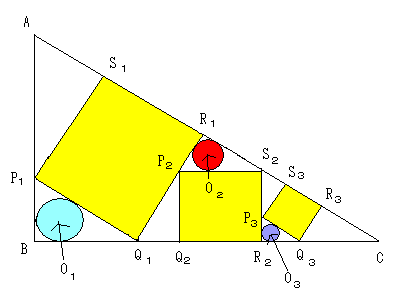
栤戣丗佢B傪捈妏偲偡傞捈妏嶰妏宍ABC偵恾偺傛偆側3屄偺惓曽宍
P侾Q侾R侾S侾丆
P俀Q俀R俀S俀丆P俁Q俁R俁S俁丂偑撪愙偟偰偄傞丅
俁偮偺捈妏嶰妏宍B Q侾P侾丆R侾P俀S俀丆R俀Q俁P俁偺
偦傟偧傟偺撪愙墌O侾丄O俀丄O俁偺偆偪
椉抂偺墌偺捈宎偑俀俆cm偲侾俇cm偲偡傞偲偒丄恀傫拞偺墌O俀丂偺捈宎傪媮傔傛丅
傑偨丄撪愙墌O侾丄O俀丄O俁偺墌偺捈宎傪倰侾丄
倰俀丄倰俁偲偡傞偲偒丄
偙傟傜偺暥帤偵娫偵惉傝棫偮娭學幃傪尒偮偗偰偔偩偝偄丅
拲丗偙偺婰帠偵娭偡傞搳峞偺宖嵹偼丄俀侽侽俉擭侾寧俈擔埲崀偲偟傑偡丅
NO.1697丂丂俙俹丗俹俛偼壗(3)丂丂丂2007.12.17丂丂丂俢俢俿
椺偵傛偭偰丄偲偵偐偔寁嶼偡傟偽摎偊偼弌傞曽幃偱偡偑丄寢壥偼堄奜偱偟偨丅
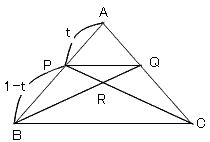
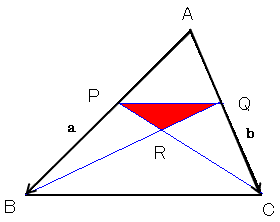 恾偺傛偆偵丄俙俛傪儀僋僩儖a丆俙俠傪儀僋僩儖b偲偟丄a丆b傪暯柺偺婎掙偵偲傝傑偡丅
俙俹亖ka丆俙俻亖kb丆0亙k亙1偲偟傑偡丅
偙傟傜傪梡偄偰丄俛俻傪捠傞捈慄俴俛偲丄俠俹傪捠傞捈慄俴俠偼丄
恾偺傛偆偵丄俙俛傪儀僋僩儖a丆俙俠傪儀僋僩儖b偲偟丄a丆b傪暯柺偺婎掙偵偲傝傑偡丅
俙俹亖ka丆俙俻亖kb丆0亙k亙1偲偟傑偡丅
偙傟傜傪梡偄偰丄俛俻傪捠傞捈慄俴俛偲丄俠俹傪捠傞捈慄俴俠偼丄
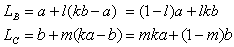
偲昞偣傑偡丅偙偙偱丄l丆m偼擟堄偺幚悢偱偡丅
俴俛偲俴俠偺岎揰俼偺埵抲儀僋僩儖r偼丄俴俛亖俴俠偲偍偄偰丄
婎掙偺學悢傪摍偟偄偲偍偗偽丄1亅l亖mk丆1亅m亖lk側偺偱丄
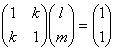
偲側傝丄
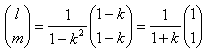
偑摼傜傟傑偡丅k亗1傪巊偭偰偄傑偡丅俴俠懁偐傜r傪媮傔傞偲丄
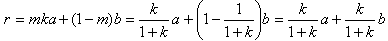
偵側傝傑偡丅偝傜偵儀僋僩儖c亖俼俹偲儀僋僩儖d亖俼俻偼丄
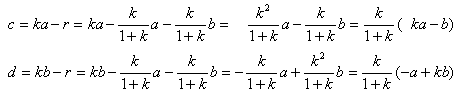
偱偡丅撪愊偺岞幃偐傜丄
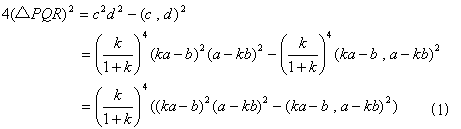
偲側傝傑偡丅
偝偰丄偙偭偐傜偑丄傗傝傖乣弌棃傞曽幃偺杮斣偱偡丅
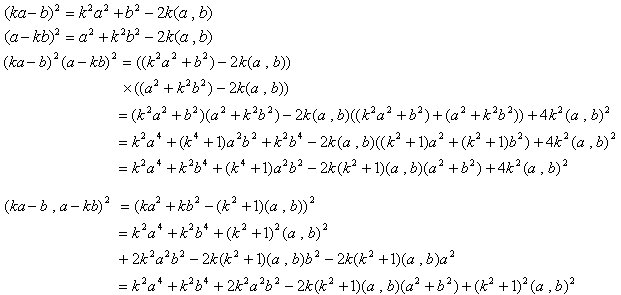
側偺偱丄
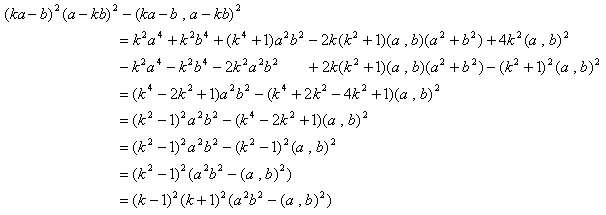
偱偡丅傛偭偰(1)傛傝丄
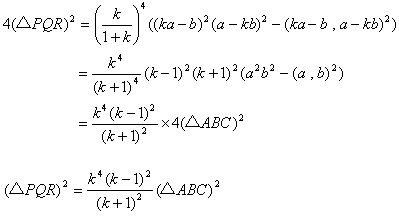
偑摼傜傟傑偡丅
廬偭偰丄仮俹俻俼偺柺愊傪嵟戝壔偡傞乽俙俹丗俹俛亖k丗(1亅k)乿偺k傪媮傔傞偵偼丄
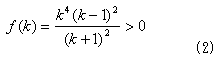
傪嵟戝壔偡傞k傪尒偮偗傟偽椙偄帠偵側傝傑偡丅偟偐偟(2)偱偼埖偄偵偔偄偺偱丄
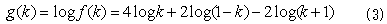
偱峫偊傑偡丅偙偙偱丄0亙k亙1偱偡丅
log偼扨挷憹壛娭悢側偺偱丄g(k)亖log f(k) 偑嵟戝抣側傜丄f(k)傕嵟戝抣偱偡丅
g(k)偺憹尭昞傪偮偔傞偨傔偵丄g(k)傪k偱旝暘偟傑偡丅寢壥偼丄
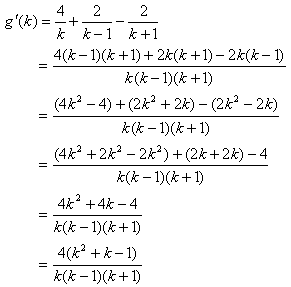
偲側傝傑偡丅g'(k)偺暘曣偺楇揰偼柧傜偐偵丄k亖亅1丆0丆1偱偡丅暘巕偺楇揰傪媮傔傞偨傔偵丄
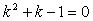
偲偍偗偽丄
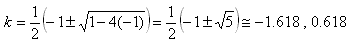
偱偡丅廬偭偰丄g(k)偺憹尭昞偼丄
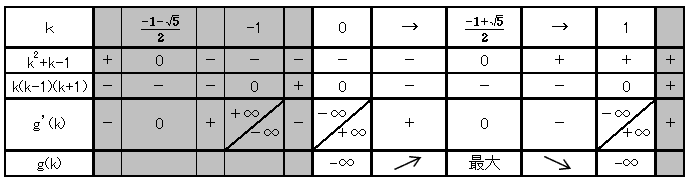
偲側傝丄仮俹俻俼偺柺愊傪嵟戝壔偡傞乽俙俹丗俹俛亖k丗(1亅k)乿偼丄
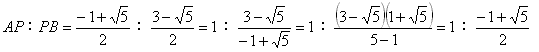
偲偄偆傢偗偱丄俙俹丗俹俛偼丄堄奜側乮丠乯帠偵墿嬥斾偱偟偨丅偝傜偵丄
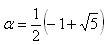
偲偍偗偽丄
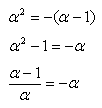
側偺偱丄
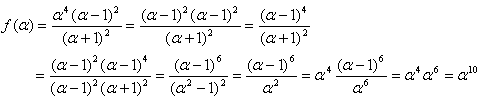
傛傝丄
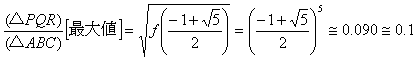
偲側傝傑偟偨丅
NO.1696丂丂俙俹丗俹俛偼壗(2)丂丂2007.12.17丂丂栭傆偐偟偺偮傜偄偍偠偝傫
仮俙俛俠偺柺愊傪俽偲偍偒傑偡丅
俙俹丗俹俛亖倲丗(侾亅倲) 偲偟傑偡丅
俹俻//俛俠側偺偱丄仮俼俛俠偲仮俼俻俹偼憡帡偱偡丅
偙偙偱丄俛俠丗俻俹亖俼俛丗俼俻亖侾丗倲 偱偡丅
仮俻俛俠偼仮俙俛俠偵斾傋偰丄崅偝偑 (侾亅倲)攞側偺偱丄
仮俻俛俠亖(侾亅倲) 亊俽
仮俼俛俠偼仮俻俛俠偵斾傋偰崅偝偑丄侾乛(侾亄倲)攞側偺偱
仮俼俛俠亖侾乛(侾亄倲)亊仮俻俛俠亖(侾亅倲)乛(侾亄倲)亊俽
仮俼俛俠丗仮俼俻俹亖侾2 丗 倲2 傛傝
仮俼俻俹亖(倲2亅倲3)乛(侾亄倲)亊俽
傛偭偰丄(倲2亅倲3)乛(侾亄倲) 偺嵟戝抣傪挷傋傟偽傛偄偙偲偵側傝傑偡丅乵掕媊堟丗侽亙倲亙侾乶
倖(倲)亖(倲2亅倲3)乛(侾亄倲) 偲偍偔偲
摫娭悢 倖乫(倲)亖{(倲2亅倲3)乫(侾亄倲)亅(倲2亅倲3)(侾亄倲)乫}乛(侾亄倲)2
丂丂丂丂丂丂 丂亖亅俀倲(倲2亄倲亅侾)乛(侾亄倲)2
倖乫(倲)亖侽 偲側傞倲偼丄倲亖侽丆(亅侾亇併俆)乛俀

忋偺昞傛傝掕媊堟偱丄倲亖(亅侾亄併俆)乛俀 偺偲偒仮俹俻俼偼嵟戝偵側傝傑偡丅
偩偐傜丄俙俹 丗 俹俛亖(亅侾亄併俆)乛俀 丗 乷侾亅(亅侾亄併俆)乛俀乸
丂丂丂丂丂丂丂丂丂丂丂亖(亅侾亄併俆) 丗 (俁亅併俆)
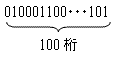


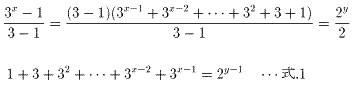

 恾偺傛偆偵丄俙俛傪儀僋僩儖a丆俙俠傪儀僋僩儖b偲偟丄a丆b傪暯柺偺婎掙偵偲傝傑偡丅
俙俹亖ka丆俙俻亖kb丆0亙k亙1偲偟傑偡丅
偙傟傜傪梡偄偰丄俛俻傪捠傞捈慄俴俛偲丄俠俹傪捠傞捈慄俴俠偼丄
恾偺傛偆偵丄俙俛傪儀僋僩儖a丆俙俠傪儀僋僩儖b偲偟丄a丆b傪暯柺偺婎掙偵偲傝傑偡丅
俙俹亖ka丆俙俻亖kb丆0亙k亙1偲偟傑偡丅
偙傟傜傪梡偄偰丄俛俻傪捠傞捈慄俴俛偲丄俠俹傪捠傞捈慄俴俠偼丄