Weekend Mathematics／問題／問題76



７６．ハイウェイ計画

ある砂漠に、一辺１００マイルの正方形の頂点に４つの都市があった。



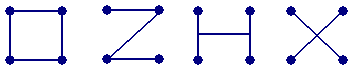
この４都市を結ぶハイウェイが計画されたが、バブル時代のＯ計画（４００マイル）は、バブル崩壊とともに、Ｚ計画（３４１マイル）、Ｈ計画（３００マイル）、Ｘ計画（２８３マイル）へと縮小された（小数点以下四捨五入）。
それでもある賢者は、「もっと短い経路がある」と言い出した。それは？










問題の出典


超々難問数理パズル
芦ヶ原伸之
講談社ブルーバックス






答えと解説





答えと解説

解答・その１

（ペンネ−ム：teki）

＜真面目な解答＞
この問題、数学では結構有名な問題で、「最短シュタイナー問題」と呼ばれてい ます。図を添付すれば分かり易いのですが、あえて言葉だけで説明します。 この場合の最短経路は、正方形の各頂点から３０°の角度で直線を引き、その交 点同士を結んでできる経路となります。 この場合の経路の長さは、正方形の１辺を１００マイルとすると１００×（１+ 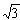）マイル≒２７３マイルですね。

正方形の場合の最短経路



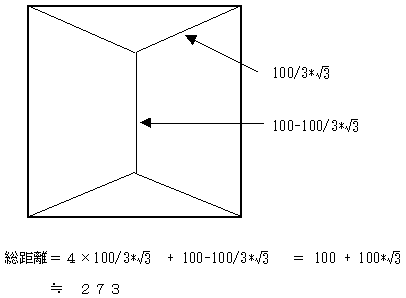
＜ふざけた解答＞
道路の幅の記述がないので、幅１００マイルの道路を造ってしまえば、長さは１ ００マイルで足りますね。 ただし、建設費はいくらになるか、保証の限りではありません(＾＾;;)



解答・その２

（ペンネ−ム：mhayashi）

答え：


＼    ／
  ＼／ 
   ｜
  ／＼     ↑
／    ＼   ↓

こういうカタチを考えました．（ん〜何計画でしょ？ (^^;）
このときハイウェイの長さは最短で 100(1+ 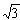即ち約 273 マイルとなる．



解答・その３

（ペンネ−ム：kiyo）

「最短シュタイナー問題」
（１+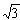）*１００≒２７３（マイル）ですね。



解答・その４

（ペンネ−ム：Y.M）






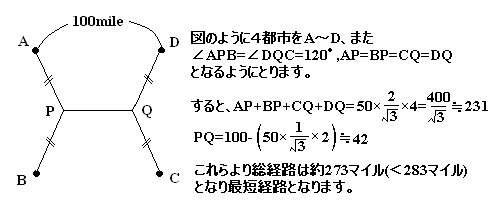
解答・その５

（ペンネ−ム：巷の夢）

解法と言っても書けません。図を描きながら、試行錯誤で見つけました。



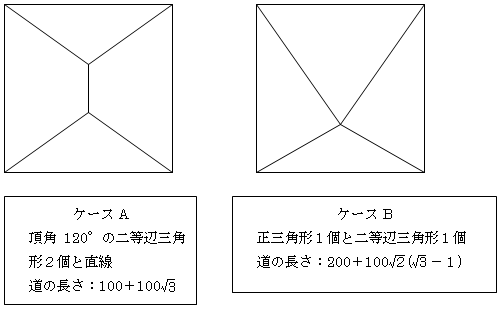
以上より、ケースAの場合に道の長さが最小になる事が分かる。



解答・その６

（ペンネ−ム：Underbird）

下の図より



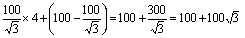
近似値は、100+173=273（ｍ）
これが最短であることは証明してありませんが、確かこうだったような。







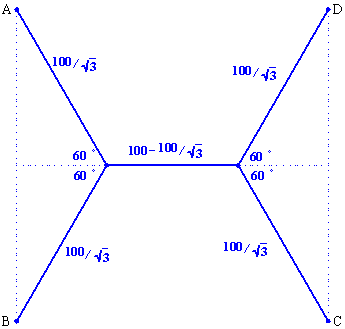
解答・その７

（ペンネ−ム：杖のおじさん）

一部変更（7/9)

BASICプログラムとエクセルで計算してみました。


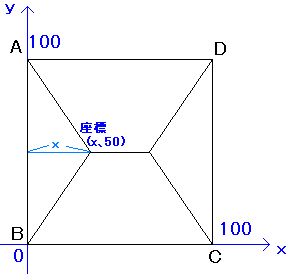
道路の長さは、ピタゴラスの定理で計算する。


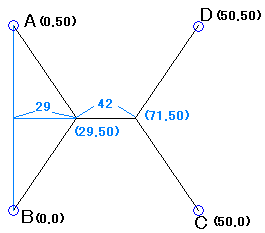
答
左の図の様な道路を作る。
道路の長さ273.21マイル

◎BASICプログラム　　カシオFX-870P、FX-890Pを使用いたしました。

10DIM X(50),Y(50)
20D=0:PRINT"ﾊｲｳｪｲ ｹｲｶｸ"
30FOR A=0 TO 50
40X(A)=INT(SQR(100^2+(A*2)^2)*200+0,5)/100+100-A*2：Y(A)＝A
41REM　PRINT　Y(A);"-";100-Y(A);"-";X(A)
42REM　INKEY$=""THEN 42
50NEXT A
60FOR A=0 TO 49
70IF X(A)>X(A+1) THEN B=X(A):C=Y(A):X=X(A+1):Y(A)=Y(A+1):X(A+1)=B:Y(A+1)=C:D=1
80NEXT A
90IF D=1 THEN D=0;GOTO 60
100BEEP:PRINT"ﾎﾟｲﾝﾄﾊ";Y(0);"ﾄ";100-Y(0);"ｷｮﾘﾊ";X(0);"Km"
110GOTO 20

ＥＸＥを押して実行すると２分８秒で次ぎの結果が得られます

　　　　　　ポイントハ　２９　ト　７１　　キョリハ　２７３．２１Ｋｍ　

と表示されます。

◎エクセルでは数式を入力します。

図１図２

　AB
1X長さ
20300
31298.04
42296.16
53294.36
64294.64
75291
・・・・・・・・・
5250282.84

→

　AB
1X長さ
229273.21
328273.22
430273.24
527273.3
631273.32
726273.42
・・・・・・・・・
520300


B2に入力した数式は次の通りです。

　　　INT((SQRT(100^2+(A2*2)^2)*200+0.5))/100+100-A2*2

B52までドラッグアンドドロップでコピーします。

Ｂ列を２行目〜５０行目までを昇順で並べ替えたのが図２です。 一番短い経路が一番上に来ます。
したがって、２９マイルの地点を通り、２７３．２１マイルと判明します。

*　計算にあたって、小数点以下の三桁目を四捨五入します。 と書き添えるべきでしたので、書き添えます。
　　（追加：2003.5.4.）



解答・その８

（ペンネ−ム：yokodon）

題意の正方形の各頂点を左上から反時計回りにＡ，Ｂ，Ｃ，Ｄとする。
辺ＡＢ、辺ＣＤの中点をＭ、Ｎとし、更に線分ＭＮ上に２点Ｐ、Ｑを、

　　　　∠ＡＰＭ＝∠ＢＰＭ＝∠ＣＱＮ＝∠ＤＱＮ＝ π/3

・・・を満たすようにとる。



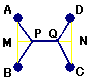
このとき、ＡＰ＝ＢＰ＝ＣＱ＝ＤＱ＝ 100/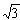(mile)
また、ＭＰ＝ＮＱ＝ 50/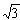 (mile) だから、ＰＱ＝ 100(1 - 1/√3) (mile)
従って、５つの線分ＡＰ、ＢＰ、ＰＱ、ＣＱ、ＤＱを結んで出来る折れ線の全長は

　　　　ＡＰ＋ＢＰ＋ＰＱ＋ＣＱ＋ＤＱ＝100×(1 +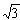) ≒273 (mile)

これは、既出４種のどの経路よりも短い。
名付けて、…何でしょうかこれは？(^^;)
#両側刺股計画？




解答・その９

（ペンネ−ム：バレー部）

今回の問題は非常に楽しませてもらいました。証明のない解答ですけれど・・・。 実は母と二人でこの問題を考えまして、私ではなく母がこの形を見つけてしまいました。

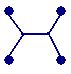こんな形でいいだろうって？

この形というのは、

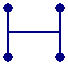から 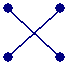に近づいていく形といえますよね。

なぜより の方が短いかというのは、

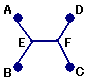
A→Cに行くとき、A→E→F→C、
B→Dに行くとき、B→E→F→D
E→Fでかぶってる！！

だからEFの長さによって、 より の方が短い時もあるようです。

最小値を求めたい。(正確じゃない気もしますが・・・。)


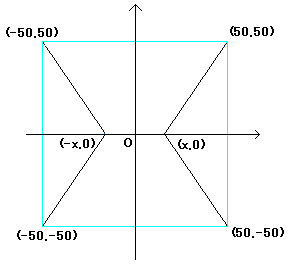
このとき

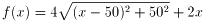　　　(0≦x≦50)

として、この関数の最小値を求めます。

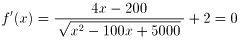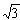　　として、　　 x=(150±50)/3

よって、x=(150-50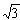)/3=63.5/3≒21のとき最小値をとりそう。
本当は正式な増減を調べなければいけないところですが、 実際に21ぐらいで275に近いくらいの値がでているのでここではOKとします。



解答・その10

（ペンネ−ム：モルモット大臣）

100m離れた４つの年を左上から時計まわりにA,B,C,Dとして AD、BCの中点をそれぞれE,Fとし、EF 上にEFの中点を対称とした点P、Qをとります。
賢者の言うより短い場合はこのPQ上のPとA,Dを結び、QとB,Cを結んだ時に生じます。


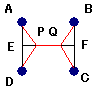
EP=FQ=X(0≦X≦50)と置くときの経路はAP=DP=BQ=CQだから4AP+PQ=F(X)とおく。
三平方の定理から

　　　F(X)=4(X2+502)1/2+100-2X

　　　F'(X)=1/2×4×2X×(X2+502)1/2-2=0より

　　　3X2=502、

　　　X=50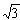/3

増減表は省略しますが X=50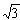/3の時F(X)=100+100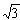=273.205≒273 よって最短経路は273mです。
この時が真の最小である証明はできませんが



解答・その11

（ペンネ−ム：ばんちゃん）

２８３マイルより短い経路が見つかりましたので投稿します。 尚、最も短い経路であるかは分かりません。 経路は下図の通りです。



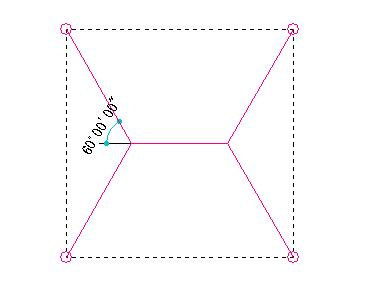
上記の形で斜線の角度が６０度の時が最短経路になりました。
この時、斜線の長さは５７．７３５マイル、中央の横線の長さは４２．２６５マイルです。
故に、経路は、４×５７．７３５＋４２．２６５＝２７３．２０５マイル（２７３マイル）
尚、中央の横線をＸと置き、全体経路をＹとすると

　　　　y=4×√(52+((100-x)/2)2)＋x

となります。この式を利用してｙが最小の時のｘを求めればよいですね。 最近は方程式なんかとは縁遠いので表計算ソフトにてｘを変化して求めました。 その結果斜線の角度が６０度の時が最短のようです。



解答・その12

（ペンネ−ム：shock8）

「＞−＜」型に高速道路を繋いで、真ん中の「−」部分の長さが (3-sqrt(3))/3 * 100 (mile)の場合

回答にいたる手順は、まず、蜂の巣型が望ましいだろうということで「＞−＜」型に 当たりをつけまして、簡略化のために正方形の一辺の長さを1にします。 それから「−」部分の長さをxとして

　　　全長 f(x) = x + 2*sqrt(1+(1-x)2)

を最小化したいので

　　　df(x)/dx = 1+(x2-2x+2)-1/2*(2x-2) = 0

を解いて導きました。



解答・その13

（ペンネ−ム：浜田　明巳）

その昔，泡の実験で見た事があります．自然界は最短距離を好む，最小エネルギーで済む事を好む．その時に見た図を頼りにプログラムを作ってみました．
答は２７３マイルでしょう．



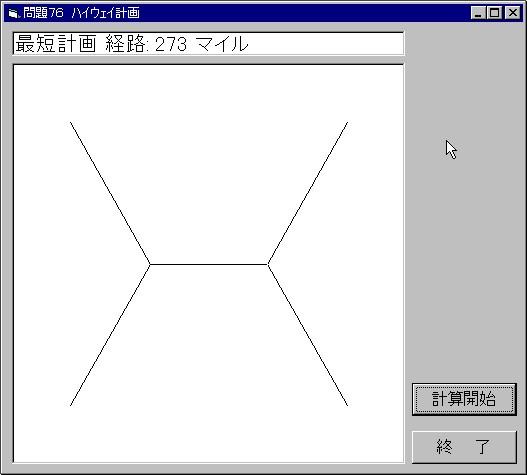
Option Explicit
Const HEN As Double = 100
Sub Form_Load()
    Dim waku As Double
    waku = HEN * 0.2
    Picture1.BackColor = vbWhite
    Picture1.Scale (-waku, HEN + waku)-(HEN + waku, -waku)
    Picture2.BackColor = vbWhite
End Sub
Sub Command1_Click()
    Dim x(3) As Double, y(3) As Double
    Dim x1 As Double, y1 As Double
    Dim x2 As Double, y2 As Double
    Dim x1_min As Double, x1_max As Double
    Dim x1_min0 As Double, x1_max0 As Double
    Dim xx1 As Double, xx2 As Double
    Dim dankai As Integer
    Dim kizami As Double
    Dim min As Double
    Dim wa As Double
    Dim j As Integer
    x(0) = 0: y(0) = HEN
    x(1) = 0: y(1) = 0
    x(2) = HEN: y(2) = 0
    x(3) = HEN: y(3) = HEN
    x1_min0 = x(0): x1_max0 = (x(0) + x(3)) * 0.5
    kizami = 1
    '
    'project ○
    Picture1.Cls
    Picture1.PSet (x(0), y(0)), vbBlack
    For j = 3 To 0 Step -1
      Picture1.Line -(x(j), y(j)), vbBlack
    Next j
    wa = HEN * 4
    Call hyouji(wa, 1)
    Call wt
    '
    'project Ｚ
    Picture1.Cls
    For j = 0 To 1
      Picture1.Line (x(j), y(j))-(x(3 - j), y(3 - j)), vbBlack
    Next j
    Picture1.Line (x(1), y(1))-(x(3), y(3)), vbBlack
    wa = HEN * (2 + Sqr(2))
    Call hyouji(wa, 2)
    Call wt
    '
    'project Ｈ
    x1 = x(0): y1 = (y(0) + y(1)) * 0.5
    x2 = x(2): y2 = y1
    Picture1.Cls
    For j = 0 To 2 Step 2
      Picture1.Line (x(j), y(j))-(x(j + 1), y(j + 1)), vbBlack
    Next j
    Picture1.Line (x1, y1)-(x2, y2), vbBlack
    wa = HEN * 3
    Call hyouji(wa, 3)
    Call wt
    '
    'project Ｘ
    Picture1.Cls
    For j = 0 To 1
      Picture1.Line (x(j), y(j))-(x(j + 2), y(j + 2)), vbBlack
    Next j
    wa = HEN * 2 * Sqr(2)
    Call hyouji(wa, 4)
    Call wt
    '
    'project minimum
    min = 10000
    For dankai = 1 To 14
      If dankai = 1 Then
        x1_min = x1_min0
        x1_max = x1_max0
      Else
        x1_min = max2(xx1 - kizami, x1_min0)
        x1_max = min2(xx1 + kizami, x1_max0)
        kizami = kizami * 0.1
      End If
      For x1 = x1_max To x1_min Step -kizami
        x2 = x(2) - x1
        wa = x2 - x1
        For j = 0 To 1
          wa = wa + Sqr((x1 - x(j)) * (x1 - x(j)) + (y1 - y(j)) * (y1 - y(j)))
        Next j
        For j = 2 To 3
          wa = wa + Sqr((x2 - x(j)) * (x2 - x(j)) + (y2 - y(j)) * (y2 - y(j)))
        Next j
        If min > wa Then
          min = wa
          xx1 = x1: xx2 = x2
          Call hyouji(min, 5)
        End If
        Picture1.Cls
        For j = 0 To 1
          Picture1.Line (x(j), y(j))-(xx1, y1), vbGreen
        Next j
        Picture1.Line -(xx2, y2), vbGreen
        For j = 2 To 3
          Picture1.Line (x(j), y(j))-(xx2, y2), vbGreen
        Next j
        For j = 0 To 1
          Picture1.Line (x(j), y(j))-(x1, y1), vbBlack
        Next j
        Picture1.Line -(x2, y2), vbBlack
        For j = 2 To 3
          Picture1.Line (x(j), y(j))-(x2, y2), vbBlack
        Next j
      Next x1
    Next dankai
    x1 = xx1: x2 = xx2
    Picture1.Cls
    For j = 0 To 1
      Picture1.Line (x(j), y(j))-(x1, y1), vbBlack
    Next j
    Picture1.Line -(x2, y2), vbBlack
    For j = 2 To 3
      Picture1.Line (x(j), y(j))-(x2, y2), vbBlack
    Next j
End Sub
Sub Command2_Click()
    Unload Me
End Sub
Sub hyouji(ByVal wa As Double, ByVal i As Integer)
    Picture2.Cls
    Select Case i
      Case 1
        Picture2.Print "○";
      Case 2
        Picture2.Print "Ｚ";
      Case 3
        Picture2.Print "Ｈ";
      Case 4
        Picture2.Print "Ｘ";
      Case Else
        Picture2.Print "最短";
    End Select
    Picture2.Print "計画 経路:"; Int(wa + 0.5); "マイル"
End Sub
Sub wt()
    Dim t1 As Integer, t2 As Integer
    For t1 = -10000 To 10000
      For t2 = -1000 To 1000
      Next t2
    Next t1
End Sub
Private Function min2(ByVal x As Double, ByVal y As Double) As Double
    If x < y Then
      min2 = x
    Else
      min2 = y
    End If
End Function
Private Function max2(ByVal x As Double, ByVal y As Double) As Double
    If x > y Then
      max2 = x
    Else
      max2 = y
    End If
End Function




解答・その14

（ペンネ−ム：夜ふかしのつらいおじさん）

答えは、ウエストのくびれた「Ｈ」計画です。（＞−＜の形）

  1. 隣の都市同士（100マイルの距離）を結ぶ計画は「Ｘ」計画(283マイル)より経路が短くなりません。

    1. ４本の「Ｏ」計画(400マイル)は明らかです。
    2. ３本の「コ」計画(300マイル)も明らかです。
      （「Ｈ」計画と同じ長さの経路です。）
    3. ２本の「＝」計画や「Ｌ」計画も明らかです。
      なぜなら「＝」計画ではあと１本足すと最短の経路が「Ｈ」計画と同じになります。
      「Ｌ」計画でもあと１本足した最短の経路は「コ」計画に戻ってしまいます。
    4. １本の「−」計画でも「Ｘ」計画より短くなりません。
      残りの２都市と結ぶとき、「Ｖ」や「Ｙ」の経路が考えられます。


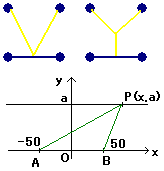
      ここで、線分ABに平行な直線上の点Pについて、PA+PBの最小値は、Pが線分ABの垂直二等分線上にあるときであることを示します。



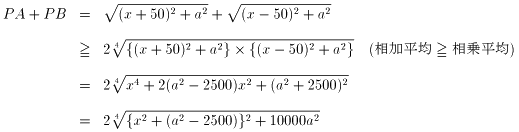
      より、x=0(PA=PB)のとき最小になるからです。
      そのとき、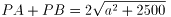　です。

      「Ｖ」の経路の場合、a=100とし、さらに100加えると、

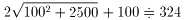      　となり、「Ｘ」計画より長くなります。

      「Ｙ」経路の場合
      　　　　

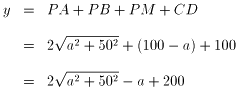
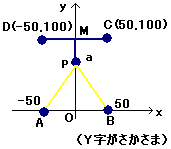
      を調べます。(0＜a＜100として)





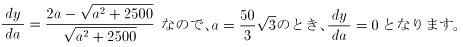
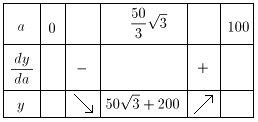
      この表より、「Ｙ」経路の最小値は、50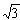+200≒287マイルとなり、「Ｘ」計画より長くなります。


    次に経路がすべて正方形の内部にある場合を考えます。 経由地の個数について注目します。

  2. ３つ以上の経路が集まるところを経由地と呼ぶことにします。
    1. 経由地を結ぶ経路は閉じない方が短くなります。
    2. 経由地は２つにまで減らすことができます。３角形の２辺の和は他の１辺より長いからです。


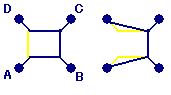
      すると、図のような経路が考えられます。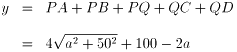

      　　　　

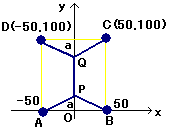
      を調べます。(0＜a＜50として)





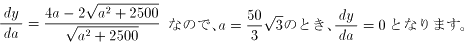
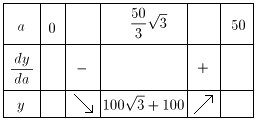
      この表より、この経路の最小値は、100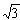+100≒273マイルとなり、「Ｘ」計画より短くなります。
      この経路を９０°回してみるとウエストのくびれた「Ｈ」計画です。






解答・その15

（ペンネ−ム：Toru）

後で使うのでまず補題から、



補題 　三角形ＡＢＣで角Ａ,角Ｂ,角Ｃ＜１２０度の時、ＡＰ＋ＢＰ＋ＣＰが最小にな るような三角形の内部の点Ｐは、角ＡＰＢ＝角ＢＰＣ＝角ＣＰＡ＝１２０度となる点 である。

略証 　三角形ＡＢＣの内部に任意の点ＰをとりＰおよびＣをＡを中心に反時計方向に ６０度回転移動し移動先をそれぞれＰ’、Ｃ’とするとＡＰ＝ＰＰ’、ＣＰ＝Ｃ’Ｐ’ だからＡＰ＋ＢＰ＋ＣＰ＝ＢＰ＋ＰＰ’＋Ｐ’Ｃ’この折れ線が直線になるときが最 小で、これから角ＡＰＢ＝角ＢＰＣ＝角ＣＰＡ＝１２０度が得られる。


さて本題へ、
４つの都市を左上から反時計回りにＡ、Ｂ、Ｃ、Ｄとする。
ハイウェイの一部が正方形ＡＢＣＤの外部にある場合は、この部分を正方形から出 る点と入る点をつないで正方形の辺上に移動することでより短いハイウェイになるの で、ハイウェイは全て正方形の辺上あるいは内部にあるとしてよい。
正方形の辺上あるいは内部に任意のハイウェイを作ったとして、このハイウェイで ＡとＣ、ＢとＤをそれぞれ結ぶルートを一つずつ選ぶ。これらは必ず存在し、この２ ルートは必ず１つ以上の共有点をもつので、これで４都市を結ぶことになって、それ 以外のルートは削除してよい。
ルートＡＣをＡからたどって最初のルートＢＤとの共有点をＰ、最後の共有点をＱ とすると、ＰＱ間のルートを直線ＰＱで置き換えてよい。（共有点が１個だけの時は Ｐ＝Ｑで点となる）
ルートＢＤはＢＰＱＤとなる場合とＢＱＰＤとなる場合があるが、対角線ＡＣを軸 に裏返してＤ→Ｂ、Ｂ→Ｄとすれば同じことであるから、ＢＰＱＤとなる場合を考え る。
するとさらにＡＰ、ＢＰ、ＱＣ、ＱＤを直線で置き換えてよく、ハイウェイの長さ Ｌは５つの直線距離の和、ＡＰ＋ＢＰ＋ＰＱ＋ＱＣ＋ＱＤで表わされ、これが最小と なるように、正方形の辺上あるいは内部の点Ｐ、Ｑを定めればよい。


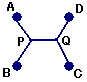
まずＡＰ＋ＢＰ、ＱＣ＋ＱＤを一定としたまま、Ｌが最小となるように、Ｐ、Ｑを 移動させる。Ｐ、Ｑはそれぞれ（Ａ，Ｂ）、（Ｃ，Ｄ）を焦点としただ円上を動く （Ｐが辺ＡＢ上あるいはＱが辺ＣＤにあるときは、それぞれ線分ＡＢあるいは線分Ｃ Ｄ上を動く）。２つのだ円が重なる時は、２つのだ円が接するようになるまでどちら かあるいは両方のだ円を焦点を変えずに小さくしてから、Ｐ、Ｑをだ円上で移動させ て、ＰＱ＝０とすればより短いハイウェイができるので、２つのだ円が（接する場合 を含め）重ならない時を考えればよい。この場合、ＡＰ＋ＢＰ、ＱＣ＋ＱＤを一定よ り、Ｌを最小にするためにはＰＱを最短にすればよいが、これは、Ｐ、Ｑがそれぞれ のだ円上で、ともにＡＢ（ＣＤ）の垂直二等分線上ある時である。
次にＡＢ（ＣＤ）の垂直二等分線上でＰ、Ｑを移動させる。ＰＱ上（Ｐ、Ｑを含む） に、点Ｒをとると角ＡＲＢ、角ＣＲＤのうち少なくとも一方は１２０度より小さいの で、たとえば角ＡＲＢ＜１２０度とすると三角形ＡＲＢに補題を適用して、ＡＰ＋Ｂ Ｐ＋ＰＲは角ＡＰＢ＝１２０度の時（この時、角ＲＰＢ＝角ＲＰＡ＝１２０度になる） に最小となる。よってＰをＡＢ（ＣＤ）の垂直二等分線上で角ＡＰＢ＝１２０度とな る点へ移動する。


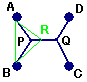
次に三角形ＤＰＣに同様に補題を適用するとＱＣ＋ＱＤ＋ＱＰは角ＤＱＣ＝１２０ 度の時、最小となるので、ＱをＡＢ（ＣＤ）の垂直二等分線上で角ＤＱＣ＝１２０度 となる点へ移動することでＰ、Ｑが定まった。


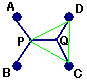
以上からＰ、ＱはＡＢ（ＣＤ）の垂直二等分線上で角ＡＰＢ＝角ＤＱＣ＝１２０度 となる正方形内部の点、この時ルートはＡＰ、ＢＰ、ＰＱ、ＱＣ、ＱＤ、あるいは対 角線ＡＣで折り返して、Ｐ、ＱがＡＤ（ＢＣ）の垂直二等分線上で、角ＡＰＤ＝角Ｂ ＱＣ＝１２０度となる正方形の内部の点、この時ルートはＡＰ、ＤＰ、ＰＱ、ＱＢ、 ＱＣのいずれかで、ハイウェイの長さはＡＰ＝Ｂ(D)Ｐ＝ＣＱ＝Ｄ(B)Ｑ＝100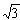／ , ＰＱ＝100−100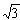／より100(1+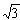) あるいは２７３マイル（小数点以下四捨五入）。




解答・その16

（ペンネ−ム：kirkland）

Ａ君「どう考えても、Ｘ計画が最短な気がするんですけどねぇ。あっ、分かりました！トンネルですよ！」
先生「はぁ？」
Ａ君「だって、地球は丸いから、地表面を道路で結ぶより、トンネルで地中を直線的に結んだ方が短いじゃないですか。【図１】」



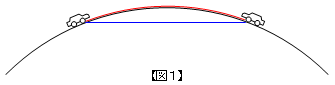
先生「トンネルを掘る方が費用がかかるに決まってるだろ！ さて、三角形ＯＡＢの内部および辺上に点ＰをとってＰＯ＋ＰＡ＋ＰＢを最小にしたい【図２】。」
Ａ君「またまた、突然ですね。」
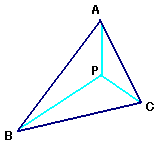
先生「ヒントをあげよう。まず、ＯＢを一辺とする正三角形ＯＢＱを外側に作る。そして、ＯＰを一辺とする正三角形ＯＰＲを図のように作ってＱＲを結ぶと……。【図３】」
Ａ君「う〜ん、△ＯＰＢと△ＯＲＱは合同ですね。というのは、Ｏを中心にＯＰ，ＯＢを60℃回転させたものがそれぞれＯＲ，ＯＱだからですね。」
先生「よろしいよろしい。もう少しだ。」
Ａ君「ということは、ＰＢ＝ＲＱです。また、△ＯＰＲは正三角形なのでＯＰ＝ＰＲです。ということは、ＯＰ＋ＡＰ＋ＢＰ＝ＡＰ＋ＰＲ＋ＲＱで、これが最小になるのは、４点Ａ，Ｐ，Ｒ，Ｑが一直線上にあるときです。このときのＰ，ＲをそれぞれＰ’，Ｒ’としましょう。【図４】」
先生「それで？」
Ａ君「△ＯＰ’Ｒ’は正三角形なので、∠ＡＰ’Ｏは120°ですね。」



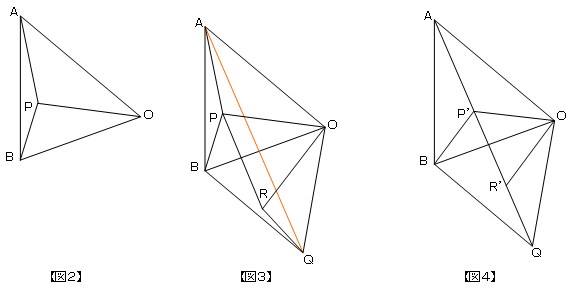
先生「いまは、辺ＢＣの外側に正三角形をつくって考えたけど、他の辺の外側につくって考えても同じ事だから、 ＯＰ＋ＡＰ＋ＢＰが最小になるのは、∠ＯＰＡ＝∠ＡＰＢ＝∠ＢＰＯ＝120°のときだね。少しごまかしたけど。」
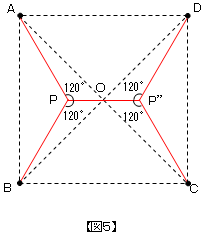
Ａ君「すると、【図５】の赤線のように道路をつくると、Ｘ計画よりも短くなりますよね。」
先生「その通り！実際の長さを求めるのは小学生には無理だからやめておこう。」
Ａ君「でも先生、この形でトンネルを掘ると、もっと短くなりますよね。」
先生「………」







これも解答でしょう

（ペンネ−ム：kunihiro）

幅１００マイルの道路なら距離も１００マイルです。
正方形の内側全部が「道路と言い張る。」これですね！



正解者

kiyo teki 巷の夢
バレー部 Toru kunihiro
ばんちゃん Y.M モルモット大臣
浜田　明巳 杖のおじさん Underbird
shock8 夜ふかしのつらいおじさん yokodon
kirkland mhayashi





まとめ

今回の問題は、「最短シュタイナー問題」と呼ばれるもので、ネットワークを組む際に経路を最短にするというきわめて現実的な問題ですね。
答えは「ウエストのくびれたＨ計画」になるわけですが、この形が最短になるということが前提になれば、変数を設定して距離を表す関数にすれば後は簡単ですが、問題はなぜこの形が最短になるかということだと思います。この説明はさほど簡単ではありません。
Toruさん、夜ふかしのつらいおじさん、kirklandさんが、その説明をしてくださっています。どうもありがとうございました。
また、 数学の部屋、 数の流れなどでも、取り上げられていますので、参考にしていただければと思います。







E-mail 戻る top