NO.1695 AP:PBは何 2007.11.26 水の流れ
皆さん、1980年の福井医科大学の入試問題です。大変興味を持ちましたから紹介します。
ただし、一部改題してあります。
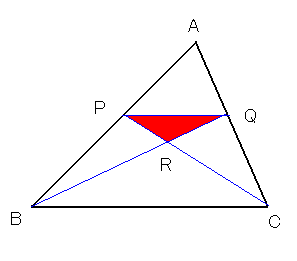
問題:⊿ABCにおいて、辺AB上の点Pを通り辺BCに平行な直線と辺ACと交点をQとする。
また、線分PCとQBとの交点をRとする。⊿PQRの面積を最大にするように
線分の比AP:PBを定めよ。
注:この記事に関する投稿の掲載は、2007年12月17日以降とします。
ColloquiumNO.225
|
皆さん、1980年の福井医科大学の入試問題です。大変興味を持ちましたから紹介します。
ただし、一部改題してあります。
問題:⊿ABCにおいて、辺AB上の点Pを通り辺BCに平行な直線と辺ACと交点をQとする。
また、線分PCとQBとの交点をRとする。⊿PQRの面積を最大にするように
線分の比AP:PBを定めよ。

注:この記事に関する投稿の掲載は、2007年12月17日以降とします。

旗の四隅に左の図のように名前をつけておきます。
・2色のときは、斜めに(あ)と(え)、(い)と(う)がそれぞれ同じ色です。
2色の入換えがあるだけなので、2通りです。
・3色全部を使って塗る場合は、ある1色を斜めに2ヶ所塗ります。
その色の選び方は、3通りです。
斜めは、(あ)と(え)の場合と、(い)と(え)の場合の2通りあります。
残った反対方向の斜めに2色を塗るやり方は、2通りあります。
だから、3×2×2=12通りです。
・4色全部使う場合は、単純な順列の4!=24通りです。
問題1
2通りです。
問題2
3色の場合は、そのうちの2色だけ使う場合と3色全部使う場合があるので
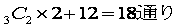
問題3
4色の場合は、そのうちの2色を使う場合、そのうちの3色使う場合、4色全部を使う場合があります。
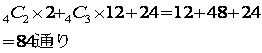
問題4
5色の場合は、そのうちの2色を使う場合、そのうちの3色使う場合、そのうちの4色を使う場合があります。
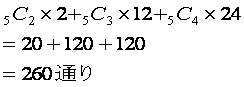
問題5
n色の場合も5色の場合と考え方は同じです。
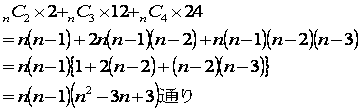
皆さん、次のような旗の4つの部分に、何色かのどれかを塗って、同じ色のものが隣り合わないようにする方法は何通りあるかを考えてください。
問題1:2種類の色で塗り分けるとき。
問題2:3種類以下の色で塗り分けるとき。
問題3:4種類以下の色で塗り分けるとき。
問題4:5種類以下の色で塗り分けるとき。
問題5:n種類以下の色で塗り分けるとき。ただし、n≧2の自然数とする。
注:この記事に関する投稿の掲載は、2007年11月26日以降とします。
今回のお題は、測定点数が非常に少ない場合の2~3次元の補間に関する事です。
これは実際に仕事で出会った問題ですが、とりあえずいつものように、まずは愚痴聞いて下さい。
以下の1.については、(独)北海道寒地土木研究所の公開データに一部基づいています。
1.背景
北海道での豊浜トンネル崩落事故以来、北海道開発局では、落石対策に関する新工法の開発が行われて来ました。
その一環として、札幌市 中の島にある (独)寒地土木研究所の構造研究室では、ここ10年ほど2層緩衝構造の実験を行っています。
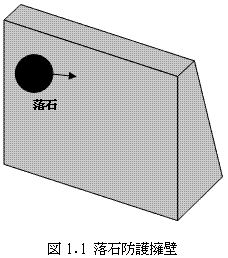
2層緩衝構造とは、落石防護擁壁に対するショックアブソーバーの事です。落石防護擁壁の概念図を図1.1に示します。
北海道の国道229号沿線には、右図のような形状をしたコンクリート壁が延々と道路沿いに続いていますが、
その多くは落石防護擁壁といわれる「待ち受け工」の一種で、図の直立した手前側の面が、落石を発生させる山側に向いています。
道路はその反対側にあります。
落石をこのコンクリート壁で受け、道路に落石を届かせないのが、その目的です。
 しかし岩の塊である落石がコンクリートを直撃すると、落石防護擁壁はたやすく破壊され、
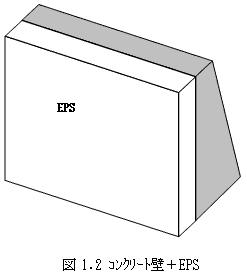
破片が道路に飛び散る事もあります。そこで考えられたのが、図1.2と図1.3に示す、2層緩衝構造です。
しかし岩の塊である落石がコンクリートを直撃すると、落石防護擁壁はたやすく破壊され、
破片が道路に飛び散る事もあります。そこで考えられたのが、図1.2と図1.3に示す、2層緩衝構造です。
2層緩衝構造はまず、コンクリート壁の前面にEPSを張ります。
EPSとは具体的に言えば、発泡スチロールです。
これによって、落石衝撃力の載荷時間を伸ばし、衝撃力の緩衝を図る事が目的です。
しかしEPSに落石を直撃させると、緩衝性能を発揮するより前にEPSがちぎれ飛び、
落石がコンクリート壁を直撃するのとほとんど変わらない状態になります(何せ、発泡スチロールですから)。
そこでEPSを保護するために、EPS材の前に、薄いRC版(鉄筋コンクリート版)を立てます。
こうして出来上がるのが、2層緩衝構造です。
 既往の実験結果によれば、落石がコンクリートを直撃した場合の載荷時間約1msecに対して、
2層構造を介した場合の載荷時間は約10倍の10msec程度に伸び、単純計算では、
この効果によって落石衝撃力は1/10に低減されて、落石防護擁壁の耐荷性能も、
相対的には10倍に上がる事が期待されます。
既往の実験結果によれば、落石がコンクリートを直撃した場合の載荷時間約1msecに対して、
2層構造を介した場合の載荷時間は約10倍の10msec程度に伸び、単純計算では、
この効果によって落石衝撃力は1/10に低減されて、落石防護擁壁の耐荷性能も、
相対的には10倍に上がる事が期待されます。
現在2層緩衝構造は、試験的に道内の数箇所で実施され、試験結果が思わしければ、
施工マニュアルの制定の後、北海道開発局の提唱する、正式な新工法として採用される見込みがあります。
以上が、2層緩衝構造の概略ですが、施工マニュアルを設計に供するためには、
落石衝撃力の定量的な把握を行う必要があります。
落石衝撃力の測定実験では、落石のかわりに所定の高さから落下させた重錘(鉄球)をRC版に衝突させます。
その際、RC版からEPS材への伝達衝撃圧力を測るために、図1.4のような形でロードセル(圧力計)が配置されます。
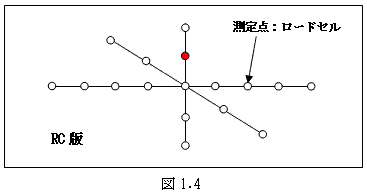 図1.4に示すように、RC版の全面を網羅するような形でロードセルを配置する事は不可能です。
これには調達できるロードセルの数の制約がまずあります。
図1.4に示すように、RC版の全面を網羅するような形でロードセルを配置する事は不可能です。
これには調達できるロードセルの数の制約がまずあります。
10m前後の高さから落下する重量数tの重錘の衝撃圧は、ふつうの水圧を測るような圧力計ではとても歯が立たず、
使用するロードセルは特注品でとても高価でした。要するに予算の問題です。
次に、その頑丈なロードセルは、大振りでした。両手の大きさに余るくらいの寸法があります。
そのために、あまり密に配置する事はできません。
最後に、その頑丈で大振りな圧力計は、言ってしまえば鉄の塊です。
RC版にそれらを余り沢山埋め込むと、鉄筋コンクリート版へのかっこうの補強材となってしまい、
本来の測定結果と違うものを測る事になります。
このような理由から、図1.4のような荒い測定点配置となり、しかもそれらの測定結果だけでもって、
RC版全面の圧力分布を予想するという、かなり無茶な問題にぶつかりました
(図中の赤点は、重錘の衝突点です)。
「どうして、こういつも測定条件が劣悪なんだ!」という気持ちはさておいて・・・。
まず考えた事は、例えば図1.4には、17個の測定点があるので、17個の係数を持つ、
2変数の多項式を用いるというものです。しかしこの方法は、以下の理由からやめました。
(1) 2変数の完全多項式を用いると、測定点数と多項式の係数の数が合致するとは限らない
(実際5次多項式が必要で、1+2+3+4+5+6=21個の係数になります)。
係数を減少させるために、不要な仮定が入る。
(2) 高次多項式の場合、過剰適合が発生する。
(3) 通常の倍精度計算では、5次以上の多項式は、桁落ち誤差の影響が大きい。
次に考えられることは、適当な低次多項式で、区分的に近似する事です。
しかしそうすると、次のような問題が発生します。
(1) 測定点に対する、区分領域の最適配置という問題が生じる。
少なくとも最初は何が正しい近似かもわからない状態で、最適化の判定基準は見当もつかない。
(2) 最適化の判定基準がわかったとしても、区分領域の配置の実行に、相当な手間がかかるのは、
目に見えている。
 結局、採用した方法は、嫌になるほど地道なものでした。
結局、採用した方法は、嫌になるほど地道なものでした。
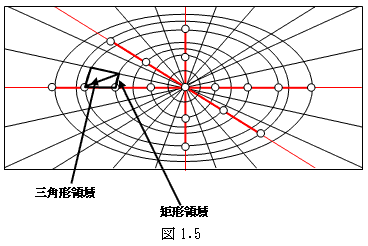
最初に、測定点を含む形で、RC版を蜘蛛の巣状にメッシュしました(図1.5)。
次に測定ライン(赤線)に沿って、2次近似を基本に測定値を補間し、
蜘蛛の巣の赤ライン上での値を埋めます。
さらにそれらの結果から横糸に沿って多項式補間し、縦糸と横糸の全ての交点での値を決めます。
それら交点で構成される矩形領域(ちょっと丸まってますが)については、
それをさらに三角形領域に分割し、三角形の3頂点の関数値を用いた線形近似により、
内部点の値を決めました。
最後に、以上のようにして決定した圧力分布を、メッシュ面積を考慮して積算して、
RC版からEPS材への伝達衝撃力を計算します。
このような計算を1回実行するだけでも、非常に難儀したおぼえがあります。
その上、衝撃圧力は時系列なので、このような計算を数千回繰り返す必要がありました。
このとき思ったのは、2次元における、メッシュフリー,多項式フリーな推定方法はないものか?、
という事でした。
2.1次元の場合
このとき念頭にあったのは、1次元時系列解析における、測定データの局所近似の考え方です。
時系列データを局所近似する場合、
大抵の関数は局所的には、多項式(w(x)=a0xn+a1xn-1+・・・+an)で近似できる. (1)
という数学的事実から、多項式近似がふつうに用いられます。
近似次数が低ければ、近似結果は角が立ちやすくなり(弱い仮定と呼びます)、
高い近似次数を採用すれば、それだけ滑らかな近似になりますが(強い仮定と呼びますが)、
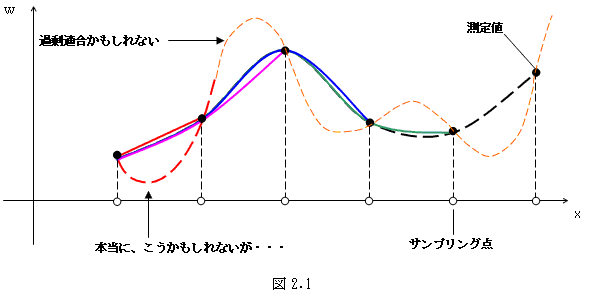
過剰適合が発生するかもしれません(図2.1)。図2.1において、緑は4次近似,青は3次近似,
ピンクは2次,赤は1次です。
ここで過剰適合について一言いうと、サンプリング点は測定状況に対して十分密に配置されているはずだ、
という前提で、ふつうは測定データを眺めます。なのでオレンジや赤点線のような近似結果だ出た場合、
離散的なデジタルデータをつなぐための仮定が強すぎたと判断します。
サンプリング間隔が適切だという前提のもとで期待するのは、黒点線にような近似です。
ですが本当は、赤点線が正しいのかもしれません。しかし測定をやり直すまで、それはわからないのです。
従って現実的に望まれるのは、できるだけ滑らかであっては欲しいが、
過剰適合にならない程度の適度な近似次数の決定です。
そこで「ベイズ-赤池の情報量最小基準」が登場します。
この基準に基づいて、弱すぎない、また強すぎない最適な局所近似の次数が決定されます。
このとき得られる結果は、付加した仮定の強さに応じて、必ず情報量が増えています。
何かを計測した時には、まず測定結果そのものを提示するのが、最低の基本です。
このときデジタルサンプリングの離散点だけでは見にくいので、とりあえず測定点間を直線で結んだりして、折れ線グラフをつくります。
原理的な話で言うと、これだけでもデータを加工している事になるのは、皆さんご存知でしょうか?。
デジタルサンプリングによって得られた原データは、図2.1の黒丸だけです。
それ以上の情報はありません。それらを赤ラインにような直線で結んでしまえば、
その中間の値を想像できるようになります(そのために、こそやってるんですが)。
原データの情報提示を越えて、こんな事が可能になるのは、事前情報(1)を受け入れるからです。
事前情報(1)を受け入れるとは、デジタルサンプリングに対して事前情報を持ち込む、
情報量の仮定の追加です。なので仮定が強すぎれば(高次な多項式を採用しすぎれば)、
異常な凹凸を発生する場合もありうるわけです。そこで原データに最も忠実であるように、
全体としての情報量を最小に抑えよというのが、
情報量最小基準と思えます。その情報量の計算を学習していないので、ここでは「思えます」にとどめます。
しかし、情報量最小基準から最後に到達する具体的な結論は、知っています。
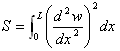 を最小化する. (2)
を最小化する. (2)
というものです。ここで積分区間0~LのLは、局所近似を行う範囲で、関数w(x)は、
その範囲内での、サンプリング点(選点)を考慮した近似曲線です。
(2)はどういう意味でしょうか?。二乗が出てきて、しかも最小化という時は、
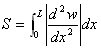 を最小化する. (3)
を最小化する. (3)
の言い換えではないかと、まずは疑ってみるべきです(最小二乗法の原理?)。
意味が同じで、||は計算しにくいので、二乗におきかえただけの場合は良くあります。
(2)を(3)の意味にとると、dw/dxは、曲線の勾配(傾き)を表し、d2w/dx2 はその変化を表すので、
(3)は、平均勾配変化が最も小さくなるように、近似曲線を選ぶべしという指示です。
もっと視覚的に言うと、できるだけ凸凹が少なくなるような曲線が最適という意味でもあります。
この意味で、図2.1のオレンジの点線は排除されます。
そして(2)または(3)は、「平均曲率最小」という事と同じです。
よって以後、「平均曲率最小」な補間方法を考察しますが、「平均曲率最小」というだけなら、
なにも1次元に限った話ではありません。
3.2次元の基本式
2次元に移り、w=w(x,y)を考えます。wの点(x,y)における全微分は、
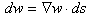 (4)
(4)
と書けます。ここで、
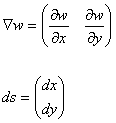
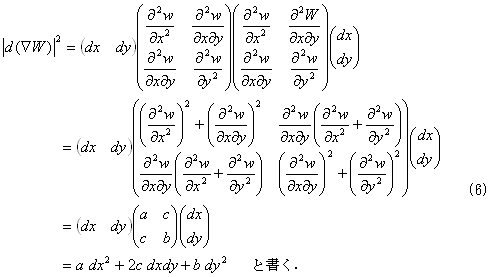
です。・は内積です。(4)から、曲率を表す(曲率情報を含む)、d(∇W)を求めます。
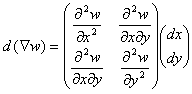 (5)
(5)
(5)の右辺第1項が小さければ小さいほど、曲面の勾配変化は小さいというのが、基本的なアイデアです。
4.勾配変化の最小化
|d(∇W)|の最小化を考えます。|d(∇W)|2は、次式です。
(6)を主方向に変換します。(dx dy)→(dx' dy')として、
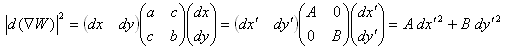 (7)
(7)
となります。(6)より a,b≧0であり、シルベスターの慣性則から A,B≧0なので、
(7)の最右辺は、次の不等式を満たします。
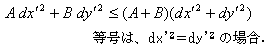 (8)
(8)
(8)の左辺において、任意の方向(dx' dy')に対して、
一つの関数w(x,y)で最小化する事は不可能なので、右辺の意味で、平均曲率の最小化を図ります。
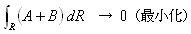 (9)
(9)
ここで A+Bは行列のtraceなので、基底変換で不変であり、A+B=a+bから、
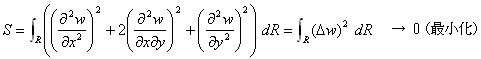 (10)
(10)
が結果として得られます。Δは、Raplasian、
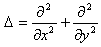
です。
5.重調和方程式の導出
積分量Sを最小化するために、(10)の変分をとり、0とおきます。Sの変分δSは次式です。
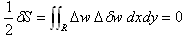 (11)
(11)
(11)に部分積分を適用すると・・・、というか、グリーンの公式の左半分を適用すると・・・、というか、
正確には、ガウスの発散公式を部分積分タイプとして繰り返し適用すると、以下が得られます。
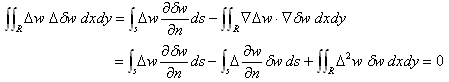 (12)
(12)
(12)において、sは領域Rの境界,∂/∂nはsの外法線方向微分,・は内積です。
(12)の2段目において、境界上の変分δwは全て0とおけるので、
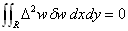
となります。さらに変分δwが、必要な回数微分可能な任意の連続関数と等価である事を使うと、
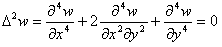 (13)
(13)
となって、重調和方程式を得ます。
図5.1にような状況に対して一般的に、(13)を満たすように推定曲面を定めれば良いのではないのか?、
というのが、ここまでの話です。
しかし偏微分方程式(13)を解くために、図1.5にようになるのは、絶対に御免です。
そこで次節では、(13)の領域R内メッシュフリーな解法の定式化を行います。
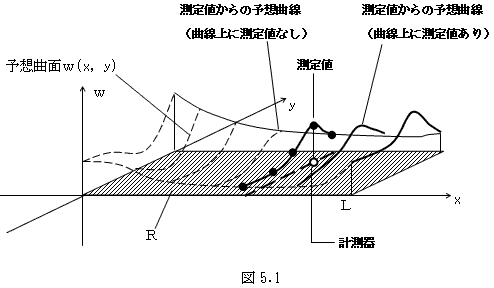
6.重調和方程式の内部メッシュフリーな定式化
重調和方程式、
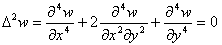 (14)
(14)
の解法を、領域内メッシュフリーな形で導きます。その準備として、グリーン関数法の弱定式化を行います。
まず、次の特殊な形の解がみつかったと仮定します。
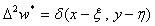 (15)
(15)
ここで δ(x-ξ,y-η)は、(x,y)=(ξ,η)に特異点を持つ、ディラックのデルタ関数です。
次に平均曲率最小の変分式の最終的な形は、次式です。
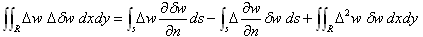 (16)
(16)
(16)において、変分δwは任意にとれる事に注意すると、δw=w* に出来ます。
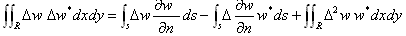 (17)
(17)
さらに(16)より、(15)のw* は次の変分式を満たす事が明らかです。
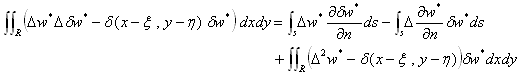 (18)
(18)
(18)においても、変分δw* は任意にとれる事に注意すると、δw*=w に出来ます。
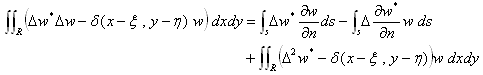 (19)
(19)
(17)と(19)の辺々引くと、次式が得られます。
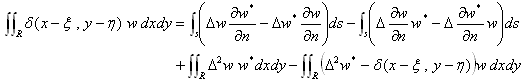 (20)
(20)
(20)に(14)と(15)を考慮すると、右辺の2重積分の項は消え、次の形になります。
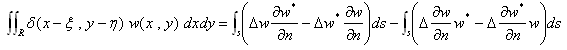 (21)
(21)
(21)において、(ξ,η)が領域Rの内点であると仮定します。このときデルタ関数の性質より、
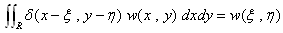
となって、(21)から、
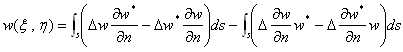 (22)
(22)
が得られます。これを内点方程式と呼びます。
ここで内点とは、測定対象である2次元領域Rの内部にある点の事です。
7.基本的な計算手順
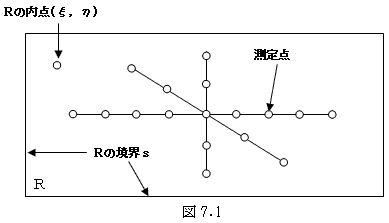 内点方程式(22)によれば、領域Rの境界s上のwの値がわかれば、
領域内の任意点(ξ,η)における、w(ξ,η)の値は計算できる事になります。
内点方程式(22)によれば、領域Rの境界s上のwの値がわかれば、
領域内の任意点(ξ,η)における、w(ξ,η)の値は計算できる事になります。
ただし(22)のw* に関しては、(15)が具体的に解けて、解が得られていると仮定しています。
ここで、2次元領域Rや、その内点(ξ,η)のイメージは、図7.1です。
基本的な計算手順は、以下となります。
最初は、測定点における測定値 w(ξ,η)の値しかありません。
そこで次の手順により、R内の任意点での値を予想します。
(1) (22)において(ξ,η)を測定点の座標に一致させ、w(ξ,η)をその点での測定値に等しいとおいて、
測定点数分の内点方程式(22)を立てる。
(2) それら内点の連立方程式から、与えられた測定値を満たすように、境界s上のwの値を逆算する。
(3) 逆算結果をもとに、領域R内の任意点での予想値を、(22)からあらためて求る。与えられた測定点では、
当然測定結果と一致します。
以上により、多項式フリー,内部メッシュフリーな形で、
測定結果に基づいた予想曲面w(x,y)を計算できると考えられます。
(22)の数値的離散化には、境界要素法(BEM)を利用できます。
境界要素法は、(22)のようなタイプの積分方程式のために開発された、数値的離散化手法です。
8.w* について
弱定式化6.と基本的な計算手順7.より、基本解 w* は、(15)さえ満たせば何でも良い事は明らかです。
できるだけシンプルな形を選びます。基本解の特異点(ξ,η) を中心とした極座標に移り、
等方的な解を求めれば容易に、
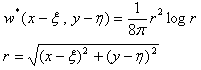 (23)
(23)
が得られます。
9.高次元へ
以上の話は、Rが2次元でなくたって可能です。
Rが3次元(x,y,z)∈Rなら、(x,y,z,w)で考えて、
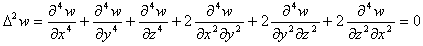 (24)
(24)
を利用できます。(22)は、
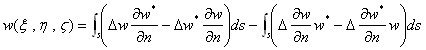 (25)
(25)
になるだけで、Rを3次元領域,sはその2次元境界です。
Rが4次元(x,y,z,p)∈Rなら、(x,y,z,p,w)で考えて、
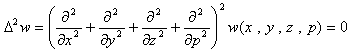 (26)
(26)
です(面倒なので展開しません)。
もちろん次元が上がれば、結果の表示には、それだけ工夫が必要になります。
例えば3次元であれば、陰線処理,シェーディング,レンダリング・・・、と問題は山積みですが、
でも例えば54次元の力学系(9質点分)の任意の4次元のポアンカレ断面の任意の3次元断面を、
自由自在に表示できるようになったら、なんて考えると、けっこう良くないですか?
(しかし・・・ポアンカレ断面にこの方法を使って、意味あるのかしら?)。
10.心配の種
ここまで安易に「平均曲率最小条件」などと言ってきましたが、重調和方程式と、
本当の平均曲率・ガウス曲率との関係はどうなってるんだろうか?。
これが心配の種なんですが、どなたかさっくり教えて頂けないでしょうか?。
微分形式と構造方程式のノートを読み返すのが面倒なんです。言い訳すると、私はプログラマーです・・・。
