
Weekend Mathematics/コロキウム室/テーマ別/44. Bezier曲線の問題
| NO.1200 | 2002.4.27. | 本多欣亮 | Bezier曲線の問題 |
Bezier曲線(ベジェ曲線)は、TrueTypeフォントやAdobe Illustrator等のソフト
で利用されている、コンピュータグラフィクスでお馴染みの曲線です。
平面上の3次Bezier曲線とは、以下の様に媒介変数表示できる有限長の曲線です:
任意の4点P1(x1,y1)、P2(x2,y2)、
P3(x3,y3)、P4(x4,y4)を与え、
x = t3 ・ x4 + t2 ・ (1-t) ・ x3 + t ・ (1-t)2 ・ x2 + (1-t)3 ・ x1
y = t3 ・ y4 + t2 ・ (1-t) ・ y3 + t ・ (1-t)2 ・ y2 + (1-t)3 ・ y1
0≦t≦1
そこで、問題です。
『互いに異なる任意の4点を与えた時、この4点で描いた3次Bezier曲線C までの距離が定数L>0である点が描く軌跡Fを求めて下さい』
『3次Bezier曲線CをL>0だけ太らせた図形Fを具体的に求めて下さい』
もちろんFをあらわす数式は1本でなく区分的で構いません。
あるいはFをあらわす近似式でも構いません。
難問だと思うので、部分的な解決でもあれば幸いです。
(補足)
Adobe Illustratorでは、F自身をBezier曲線であらわしています(「パスのオフ
セット」コマンド)。
が、これはたぶん近似でしょう。厳密にはF自身はBezier曲線ではあらわせない
と思います。

| NO.1201 | 2002.5.1. | yokodon | Bezier曲線の問題(2) |
Bezier 曲線C上の点を (x(t), y(t)) 、求める軌跡F上の点を (X,Y) とします。
「曲線と点の距離がLである」とは、「点から曲線上のある1点に下ろした垂線(線
分)の長さがLである」という意味であり、「曲線とある直線が直交する」とは、「
その直線と曲線の交点における曲線の接線を考えたとき、交点において接線と件の直
線が直交する」という意味であるとして考えます。
t を固定すると、C上の点 (x, y) における法線ベクトルは (-dy/dt, dx/dt) で
表せるので、(X, Y) としては以下のようにとればいいことになります。
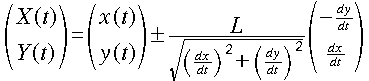
上式第2項が“太らせ”た部分になりましょうか。第2項が“±”になっているの
は、法線を伸ばす方向が平面上で2つあることによります(単位法線ベクトルの L
倍)。これを t の式に書き直しても、綺麗な形にはならなさそうですね。
想定している『距離』の取り方が違ってましたら、スミマセン。

| NO.1207 | 2002.5.2. | 本多欣亮 | Bezier曲線の問題(3) |
yokodonさん、一般型の提示ありがとうございます。
題意はその通りで間違いありません。
実際のソフトウエア(Illustrator)では、かなり高い精度で“太ら
せた”図形を、別の複数の3次Bezier曲線で“近似”している様です
(しかも計算時間はかからず、殆ど瞬時に)。
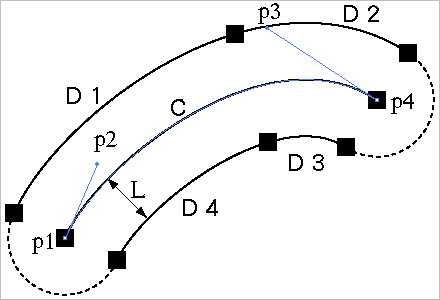
両端が半円弧(破線部)であることは題意から自明。
問題はそれ以外の部分で、この例ではIllustratorは4本の3次Bezier
曲線(D1〜D4)で“近似”している模様。
この近似曲線の構成法が具体的に判る方、いらっしゃいますか?
当方、Bezier曲線の形状を変えずに細分割する方法(こちらは厳密解)
などは、書籍を探し出して発見できたのですが、この問題のように
“(近似)オフセット”するアルゴリズムはいまだ観たことが
ありません。
もし、自由曲線や近似理論に詳しい方がおられましたら、引き続き
アイデアをお願いします。

| NO.1209 | 2002.5.5. | DDT | Bezier曲線の問題(4) |
No.1207でIllustratorが、4本の3次Bezier 曲線(D1〜D4)で、
"どのように"近似しているかの模様はわかりません。
もしIllustratorの正規ユーザーでいらっしゃるなら、
マニュアル付属の技術資料かオンラインのホワイトペーパーなどに書かれていないでしょうか?。
「自由曲線や近似理論に詳しい方がおられましたら、引き続きアイデアをお願いします(原文のまま)」
ですが、"詳しくない"のですが、じつは私はAutoCadユーザーです。
AutoCadは、いちおう世界一ユーザー数の多い製図道具と言われております。
拡張仕様を持たない素のAutoCadでは、自由曲線の拡幅(オフセット)を以下のように行います。
(1) まずAutoCadで自由曲線は、ポリラインから出発します(要するに折れ線です,図-1)。

(2)ポリラインを曲線化するには、ポリライン編集オプションのスプラインか、
フィットラインを用います。スプラインオプションはポリラインを、
図-1の折れ線の折れ点をコントロールポイントするスプラインに変えます。
このスプラインがBezier 曲線であったかどうかは自信ありません。
フィットラインも折れ点をコントロールポイントとして、最も滑らかにつながる円弧の集合にします。
図-2は、Wordのオートシェイプで書いた図なので、正確な再現ではありません。
(3)重要なのは素のAutoCadでは、図-2の自由曲線をオフセットしようとした場合、
そのままではできないという事実です。図-2の曲線をオフセットするには、
いったんスプラインまたはフィットラインオプションを解除して図-1のポリライン状態に戻し、
そこでオフセットします。オフセット後は図-3のようになり、
ポリラインを構成する直線セグメントのオフセットが交わらなければ延長して交点をつくり、
セグメントが交われば、そこでオフセットセグメントをトリムして、
図-4のオフセットポリラインをつくります。
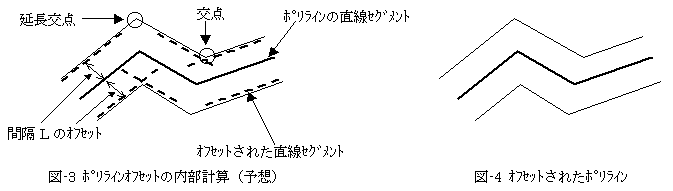
(4)結局、図-4の状態の3つのポリラインに曲線化オプションをかけて、
自由曲線の近似オフセットをつくります。

(5)いちおう世界一ユーザー数の多い製図道具と言われているAutoCadの虎の威を借りて言うと、
このような方法で得られた自由曲線の近似オフセットに不自由を感じたことはありませんし、
実用的だと思います。この方法は実質的に、
もとのBezier 曲線のコントロールポイントだけをオフセットして、
そこにBezier 曲線を引くだけですので、もしBezier 曲線を発生するアルゴリズムをお持ちなら、
そんなに難しい計算ではないと思います。もっとも研究目的などで高精度が必要なら、
明らかに精度不足です。

| NO.1210 | 2002.5.6. | 本多欣亮 | Bezier曲線の問題(5) |
DDTさん、回答ありがとうございます。
ちなみに私は正規ユーザーですが、Illustratorの場合、マニュアルには内部
処理までを詳しく述べた技術資料は付いていませんし、私が調べた範囲では
オフィシャルのプログラマ向けテックノートにもそのあたりのアルゴリズム
を解説したものは観たことがありません。

| NO.1225 | 2002.6.6. | prospero | Bezier曲線の問題 (6) |
かれこれ15年程前, この問題について考えたことがあります. といっても,
数学の問題としてに考えたのではなく, コンピュータプログラムでどう実
現するか, ということです. ですから, 証明もしていませんし, けっこう
いいかげんですが, 参考になるかと思いますので, 少し説明します.
当時, Adobe がその総力を結集して(?)世に送り出した PostScript を詳
しく調べれば分かるのですが, PostScript では Bezier 曲線を太らせた
曲線を作るために Bezier 曲線を細かな線分に分割し, それを太らせてい
ます.
なぜか?
PostScript では, Bezier 曲線を描画するのに, 本多様が示された, パラ
メータを使った式をそのまま用いるのでははく, 1 つの Bezier曲線を 2
つに分割する操作を, 分割された各部分が十分小さくなるまで繰り返すこ
とによって折れ線近似するという方法を取っています. 1 つの Bezier曲
線を 2 つに分割する操作は, 加減算と 2 で割るという作業だけでできま
すから, 当時の非力なコンピュータにとっては, この方法は極めて有効だっ
たわけです.
Bezier 曲線を太らせた曲線が高精度に Bezier 曲線で近似できる方法が
あれば, Bezier 曲線を細かな線分に分割してからそれを太らせる必要は
ありません. なぜなら, その方が塗り潰す領域を囲む線分の数が 1/3 ぐ
らいに減り, そうです!, 当時の非力なコンピュータにとっては一層有利
な方法であったはずだからです. しかし, Adobe の頭能を持ってしても線
分を太らせる方式を選ばざるを得なかった理由は, それができなかったか
らなのだと私は推測しています.
もし, 様々な PostScript をお使いになれる環境がおありでしたら, 以下
のプログラムを試してみて下さい. 多くの PostScript の実装で, 線分を
太らせる方式が用いられていることが確認できるはずです.
%!PS 0 0 moveto 72 0 0 72 72 72 curveto 10 setlinewidth strokepath 0 setlinewidth stroke showpage
なお, 線分を太らせる方式の場合, 凸の部分でも凹の部分でも太らせた端
の部分を隣の線分の太せた端の部分と繋ぐだけで良いので, アルゴリズム
は簡単です. ただし, 塗り潰す時に, non zero で fill するのは重要で
す. eo-fill すると線分の内側に塗り残しができます.

| NO.1226 | 2002.6.22. | 本多欣亮 | Bezier曲線の問題 (7) |
prosperoさん、興味深いお話と貴重なコードの提示ありがとうございまし
た。PostScriptのクローンインタプリタ(LEGATOSCRIPT)が使えるので、
参考にさせていただきます。

| NO.1357 | 2003.2.13. | 本多欣亮 | Bezier曲線の問題(8) |
昔投稿した
「Bezier曲線の問題(オフセットしたベジェ曲線の座標を求める計算方法)」ですが、今日すばらしい資料が見つかったよ:
私家版BEZIER講座(pdf)
未解決な部分もあるようだけど、かなり参考になります!

| NO.1423 | 2003.11.5. | 本多欣亮 | Bezier曲線の問題(9) |
Bezier曲線の問題(9) 【完結編】
与えられたBezier曲線のオフセット曲線を、精度良くかつ構成的に近似で求める
問題ですが、近似オフセット曲線自身をBezier型式で表現するアルゴリズムを解
説した論文が見つかりましたので、ご報告します。
Computer Aided Geometric Design Vol.5, No.1, June 1988, pp.33-40
"Spline Approximation of Offset Curves", J. Hoschek
コロキウム室NO.1200の記号を使ってアルゴリズムの粗筋を書いてみると:
【1】 P1、P4(端点もしくはアンカーポイントと呼ばれる)のオフセット点は
その点での法線方向にLだけ移動した点であり自明。
【2】 P1、P4以外で曲線 C上のいくつか(個数は論文中で明示)の点を選び、
上と同様にオフセット点を求める(当然厳密に求まる)。
【3】 ベクトルP1→P2、ベクトルP3→P4 の2つのベクトルは、それぞれが並
行で長さの異なるベクトルに移される(ベジェ曲線の定義より明らか)。これら
の2つのベクトルの比例定数をそれぞれλ1,λ2とする。
【4】 最小2乗法を使ってλ1,λ2の最適解を見つける(最適化する関数や制
約条件は論文に明記されている)。
【5】 最小2乗法では【2】の点を選んだときの tの組み合わせに依存するの
で、これを選び直すかどうか考慮する(※1)。その後で残差(定義は論文中に
明示)を計算。
【6】 予め定めた誤差範囲に残差が入れば完了。予め定めた反復限度回数に達
していなければ【4】に戻る、そうでない(反復回数を超えている)場合は、与
えられたBezier曲線を二分割(※2)して、分割したそれぞれの曲線で【2】か
らはじめる(つまり、再帰的に計算する)。
サブルーティンとして使われている※1は、J. Hoschek自身の他の論文で(上記
論文のpp.40 References に掲載)、※2は、書籍「CAGD のための曲線・曲面理
論」共立出版株式会社刊、もしくは、私の書いたサンプルコード(両者同内容)
http://www.hi-ho.ne.jp/kakky/c_tb/source/src01.html#AIPlug-in
で見ることができます。また、非線形関数の最小2乗法についてはいろんな教科
書に載っていますね。
Adobe Illustrator がこの論文の方法でBezier曲線のオフセットを計算している
かどうかはわかりませんが、オフセット後にコントロールポイントの個数がオリ
ジナルの曲線に比べ増加する現象があるあたり、いかにも上記【6】の再帰計算
でもしていそうな感じです。

 戻る
戻る