
Weekend Mathematics/コロキウム室/NO.160
| NO.1340 | 2003.1.1. | Junko |

|
2003年のお正月、あけましておめでとうございます。
昨年もたくさんの方々に励まされ、助けられた1年でした。
本当にどうもありがとうございました。
そのおかげで、楽しい時間を過ごすことができたと思います。
日頃「人生、年を追うごとにおもしろくなってくる」と突っ張って言っている手前、
今年も昨年以上に充実した年にしたいと思います。がんばりまーす!!
(画像提供 LITTLE HOUSE)

| NO.1341 | 2003.1.4. | 水の流れ | Tanのn倍角 |
太郎さんは、先日生徒から、「三角関数のsin3θをsinθ、 cos3θ をcosθ で表す3倍角の公式があるのに、tan3θをtanθで表す公式はないのですか。あれば、教えてください。」という質問を受けました。そのときは、私の見たことがないから、「必要なら、自分で作ったら。」。と言っておきました。このことを、問題にします。tanθ=t とおくとき、次の設問に答えてください。
(1)tan2θをtで表せ。(これは公式ですから、結果だけでいいです。)
(2)tan3θをtで表せ。
(3)tan4θをtで表せ。
(4)tan5θをtで表せ。
(5)今までの答えから、類推して、tannθをnとtで表せ。
(6)(5)の予想が正しいことを数学的帰納法で示してください。
追加(7)実はこの計算をしていたら、分母、分子の係数が有名な数列になっていることに気がつきました。必然性があるのでしょうか。疑問に思っています。どなたか 教えてください。

| NO.1342 | 2003.1.5. | DDT | ガウスの発散定理の応用(5) |
ガウスの発散定理の応用(2)は、全て理解もしていないくせに、けっこう知ったかぶりして書きました。「ガウスの驚異の定理」は、かつさんのおっしゃる通り、曲率についてのお話です。職業柄「測量」が身近にあるもので、直接測れない曲率を、直接測れる「距離の変化」におきかえてしましました(言われてみれば、曲率を距離の変化におきかえて良いんだろうか?)。いずれにしろ正確な姿を伝えて頂きありがとうございます。
「驚異の定理」に気づいたガウスが、図形は図形自身で形を決められる事にも気づいて、累次積分の発散形式への定式化に向かったのだとしたら・・・そんな事を考えていたら、なにかわくわくして知ったかぶりしてでも書きたくなった、というのが本音です。

| NO.1343 | 2003.1.5. | DDT | 単射と全射 |
こんな事を知っていても、僕自身の仕事には何の利用価値もないし、たぶん受験にも役立たないのだけれど(最近高校生のかたも読んでると知ったので)、大学時代に当時としては(今でも?)最先端の情報幾何学コースをとった友人が、いきなり圏論をやらされて、次のような問題をもってきました。
1.単射の定義
XとYとZを任意の集合,fとgとhは写像で、f:X→Y,gとh:Z→Xとする。
f ○ g=f ○ h
なら必ずg=hとなるとき、fを単射という。ここで ○ は、写像の合成を表わす。
2.全射の定義
XとYとZを任意の集合,fとgとhは写像で、f:X→Y,gとh:Y→Zとする。
=h ○ f
なら必ずg=hとなるとき、fを全射という。ここで ○ は、写像の合成を表わす。
ここであえて定義を問題と言ったのは、上の定義を読んだ瞬間、書かれた内容を証明するまで意味を理解できないと思ったからです。その友人は、数学の授業で決して手を抜かなかった人(むしろ数学好き)で、単射と全射のふつうの定義くらいご存知でしたが、線形代数の初歩と陰関数定理あたりでアップアップするのが学部生の現状です(私の出身大学では)。それをいきなり圏論とは、ゼミの先生もずいぶん無茶をなさるものだと思ったりしました。この時は、なんとか応えをひねり出せたのですが、いまいちしっくりした証明になりませんでした。そこでこの場をお借りして、皆さんの意見をきいてみたくなり、問題形式で提出しますので、よろしくお願いします。以下、1.と2.を証明するための誘導形式にしますが、もちろんこの路線に乗らなくても結構です。
まず念のため、単射と全射をふつうに定義します。
定義1.単射
f:X→Yとして、x1,x2∈Xとする。x1≠x2なら、
f(x1)≠f(x2)
であるとき、fを単射という。
定義2.全射
f:X→Yとして、任意のy∈Yについて、
y=f(x)
となるx∈Xがあるとき、fを全射という。
さらに像と逆像を定義します。
定義3.逆像
f:X→Yとして、一つのy∈Yをとり、y=f(x)を満たすx∈X全体の集合をf-1(y)で表わし、fによるyの逆像と呼ぶ。明らかにf-1(y)⊂Xであり、f-1(y)=φも許す。Y全体の逆像を考えたいときは、f-1(Y)と書き、A⊂Yの逆像を考えたいときも、f-1(A)と書く。
定義4.像
f:X→Yとして、一つのx∈Xをとり、y=f(x)を満たすy∈Y全体の集合をf(x)で表わし、fによるxの像と呼ぶ。明らかにf(x)={y}⊂Yである。X全体の像を考えたいときは、f(X)と書き、B⊂Xの像を考えたいときも同様。
問1.
定義3,4を用いて、定義1,2を書き直せ。
次に左逆写像(引き込み)と右逆写像(切口)を定義します。
定義5.左逆写像
f:X→Y,r:Y→Xとする。
r ○ f=IdX
となる写像rがあれば、すべて写像fについての左逆写像という。ここでIdXは、X上の恒等写像。
定義6.右逆写像
f:X→Y,s:Y→Xとする。
f ○ s=IdY
となる写像sがあれば、すべて写像fについての右逆写像という。ここでIdYは、Y上の恒等写像。
問2.
| 定理1. (1) fが単射 ⇔ 左逆写像がある。 (2) fが全射 ⇔ 右逆写像がある。 |
問3.
右逆写像を使って、双射を特徴づけよ。ここで双射とは、写像fが全単射であること。
問4.
定義1.と2.を示せ。定義なのに、「示せ」とは変ですけど。

| NO.1344 | 2003.1.9. | Hkeisuke | 最速降下問題(13) |
投稿を見ていて最速降下問題に関するものがありましたが、これは、mg(一定)という力場での最速降下線を見つける問題でした。
そこで他の力場でも同じような問題が考えられるのではないかと思い、万有引力
の場合ではどうなるかを考えていたのですが、どうもうまくいかないので、考え
てみてほしいです。問題を文にすると、
ということです。万有引力下で、ある点Aから点Bに移動するのに最短の時間で移動するような曲線 を求めよ。

| NO.1345 | 2003.1.12. | Junko | 単射と全射(2) |
問1
定義1
Xとf(X)がfにより1対1に対応しているということでしょうか?
もっときれいな表現があるのかな?
定義2
Xの像がYと一致するということですから、f(X)=Y
問2(定理1の証明)
(1)f(x1)=y1,f(x2)=y2とする。
○ fが単射であるとする。
x1≠x2ならば、y1≠y2であるから、
f(X)に属する任意のyについて、ただ1つのxが存在して、f(x)=y
従って、r(y)=x と定義すれば、 r○f(x)=r(y)=x となり、 r○f=IdX
rはfの左逆写像となる。
○ 逆に、fに左逆写像rが存在すれば、r○f=IdXだから、
x1、x2(x1≠x2)に対して、 r(y1)=x1、r(y2)=x2となる。
rは写像であるから、当然y1≠y2である。つまりfは単射である。
(2)
○ fが全射であるとする。
Yに属する任意のyについて、Xに属するxが存在して、f(x)=y
従って、s(y)=xと定義すれば、 f○s(y)=f(x)=y より、 f○s=IdY
○ 逆に、fに右逆写像sが存在すれば、 f○s=IdYだから、
Yに属する任意のyについて、s(y)=xに対して、f(x)=yとなる。
従ってfは全射である。
とりあえずここまでということで。

| NO.1346 | 2003.1.12. | WHORYU | 最小値が取り得る最大値(1) |
友達から質問されて長く考え中の問題があります。
皆様方からご教示いただければ幸甚です。
7*7mの正方形の的があり、これに50個の弾があたりました。
1.着弾点の2点間の距離の最小値はルート2m以下であることを示せ。
(ただし、ルート2mとなる場合があるかどうか、即ち「以下」か「未満」かは微妙です。)
2.任意の2点間の距離の最小値が取り得る最大値をもとめよ。
(上記1.でルート2mとなる場合が存在すれば、本問の答えはルート2m。しかし、もっと小さい値であると予想される)
3.上記問題で、49個当った時、任意の2点間の距離の最小値が
取り得る最大値をもとめよ。
さらに簡単な場合を考えれば、正方形の1辺の長さを1とし、
4.2個当たったときはどうか
(当然ルート2m)
5.3個の場合
(これは難しい。ルート(1+1/64)の場合がありますが、もっと大きい場合があるか不明です。)
6.4個の場合
(当然1)

| NO.1347 | 2003.1.13. | スモークマン | 最小値が取り得る最大値(2) |
1)は簡単。
鳩ノ巣の論理から、1m四方の区画が49個あると考えられるから、そこに50個入れると、どの区画かには2個の点が入ることになるから、その中では、√2以下しか離れられないことが分かる。
2)これは、最大に離れた2点を取ったとき、その他の点との距離がいずれもそれ以下にならないということだから、まず49個の点を、49区画の正方形のそれぞれの真ん中に配置する。この時、各点間は、当然1mが最小であり、ずれたら、それ以下になるから、最小値の最大でなくなる。この配置に、もう1点を加えるとき、一番近い同士の4点(返1mの正方形)の中心が、最大に離れたこととなる。つまり、√2/2
3)2)で考えた通りで、1
4)√2
5)正方形に内接する正三角形になる。
どれが最大になるか良く分からないですが、一つの頂点を含むものは、一辺が、2√(2-√3)≒ 1.0352 となりそうです。
6)1

| NO.1348 | 2003.1.18. | wasmath | 単射と全射(3) |
圏論における単射と全射について、整理してお話したいと思います。
先の記事では、誤解と混同があるようです。

以下、集合の圏(対象が集合、射が写像)の場合だけを考える。


この定理の結果、集合論においては1対1写像のことを単射、上への写像のことを全射と呼んで差し支えないことになります。しかし、より本質的なことは、「1対1写像」や「上への写像」
のように集合の要素に依存するかに思える概念が、「単射」や「全射」といった
集合(object)と写像(morphism)のみに依存する概念として規定できるということです。
これはごく一部ですが、本質を抽象して枠組みだけで論じられるところが圏論の威力と魅力だと言えます。

| NO.1349 | 2003.1.18. | 水の流れ | カバリエリの原理 |
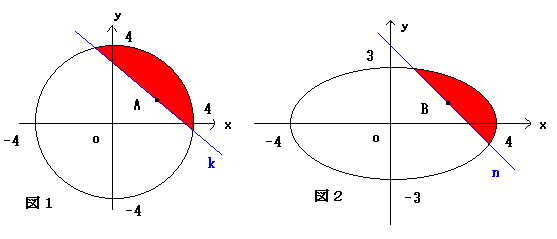
太郎さんは、先日生徒に、カバリエリの原理「2つの平行な面のあいだにはさまれた2つの図形であって、それに平行な平面で切った切り口の面積がいつでも等しければ、両方の体積は等しい」ことを説明し、「この考えは面積にも利用できるぞー」と話しました。ここで、次の問題を考えてください。

(修正 1/20 9:30)

 E-mail
E-mail
 戻る
戻る