
Weekend Mathematics/コロキウム室/NO.146
| NO.1244 | 2002.8.4. | kiyo | ぞろ目(2) |
十進ベーシック(1000桁モード)で探索しました。
REM ぞろ目 2桁-1000桁
FOR M=2 TO 1000
LET S1=2*(10^M-1)/9
FOR A=1 TO 9
LET S=S1*A
LET N=INT(SQR(S))
LET S2=N*(N+1)
IF S=S2 THEN
PRINT N;S/2
END IF
IF M=1000 AND A=9 THEN
PRINT N
PRINT LEN(STR$(N));"桁"
LET N1=N
END IF
NEXT A
NEXT M
PRINT N1*(N1+1)/2
END
N*(N+1)=2*A*(10^M-1)/9
0<A<10, 1<M
N=?
M=2 (10^2-1)/9=11
A=5 2*5=10, 10*11 (1)
A=6 2*6=12, 11*12 (2)
M=3 (10^3-1)/9=11=3*37
A=6 2*3*6=36, 36*37 (3)

| NO.1245 | 2002.8.5. | DDT | 空間上の円を動く2点(4) |
NO.1230のyokodonさんよりもっと今更ながらなのですが、
間違えました。題意の取り違えです。
この間違いパターンは、中学校で算数が数学に変わって以来、何度も失敗したパターンですが、
いまだに直ってないようです。
Junko先生は常々「答えに到達するまでの過程を書け」と言っておられるので、
ここではそれを悪用して、なぜ間違ったのかについて言い訳をした上に、最後に愚痴をこぼします。
(1)NO.1196 問題オリジナル
xyz 空間において、xy 平面上の円C:x2 + y2 = 1, z = 0 と、 yz 平面上の点P(0, u, v) (u > 1, v ≠ 0)を与える。更に、円Cの周上に点Qをとり、 直線PQと xz 平面の交点をRとする。
点Qが円Cの周上を動くとき、点Rの描く軌跡が xz 平面上の円になったという。 u, v の満たすべき関係式を求めよ。
(2)NO.1196 の間違えた読み方
xyz 空間において・・・中略・・・交点をRとする。
任意の(0, u, v)に対して、点Qが円Cの周上を動くとき、 点Rの描く軌跡が xz 平面上の円になった。u, v の満たすべき関係式を求めよ。
(3) (2)に対するふつうの表現
xyz 空間において・・・中略・・・交点をRとする。点Qが円Cの周上を動くとき、 点Rの描く軌跡が xz 平面上の円になった。u, v の領域を求めよ。
(5) 個人的に最もわかりやすいNO.1196の表現
xyz 空間において・・・中略・・・交点をRとする。
各(0, u, v)に対して、点Qが円Cの周上を動くとき、点Rの描く軌跡が xz 平面上の円になった。
u, v の満たすべき関係式を求めよ。
です。こっちの方が、可能な(0, u, v)のそれぞれに対して、
(x,z)の軌跡がそれぞれ円になることがよりわかるような気がしますが、
やはりこれは言い訳です。
(4)のような早とちりを回避する最も素直な方法は、
NO.1230のyokodonさんのやり方で正直に計算することです。
つまり、
鉄則1: 計算して片付くなら計算しろ!。 計算して片付くとわかるのは、とても幸せなことだ。 ショートカットはその後で。じつは自分の解答にちょっと腑に落ちないところがありました。 それは問題の付加条件(u > 1, v ≠ 0)が、解答の決定打にならなかったからです。 このような付加条件は、計算が余りにも煩雑になったりしないように配慮した、 試験官の良心のようなものだと思っています。そこで、
鉄則2: 問題の条件を使い切れなかった時は、間違えてると思え!。
寺田の鉄則ではありませんが(古いかな?)、鉄則1,2はやはり正しいとあらためて思いました。
では愚痴です。
高校では、(5)の各何々表現を何故使わないのだろう?(注:現在の高校のことは知りません)。
とっつきやすい表現ではありませんが、一度納得してしまえば意味は明瞭です。
(1)の言い方の中に、「(0, u, v)のそれぞれに対してそれぞれ円になるとは、
一言も書いてないじゃないか!。題意が不明確だ!」と言いたくなった受験生はきっと
いると思うのです。一理ありますが、厳しく言えば一理あるだけです。
「(0, u, v)が領域として変化しうると思ったのに(つまり題意よりも広い条件を仮定したのに)、
なぜ(x,z)の軌跡の条件だけを固定したのだ?。それは題意に含まれない条件だ」
と言われたら、それまでです。ですが、解の可能性をできるだけ広くとり、
変化しうる解候補に対して不変な制約条件を見抜いて、
系の構造を取り出すという感覚は推奨すべきだと思います。
こんなことを言うのは「題意が不明確だ!」と言える受験生は、
まだ救われるほうだと思えるからです。(1)に関して(2)と(5)の区別が最後までわからず、
結局そんなことが原因で数学を離れる人達は結構いるんじゃないでしょうか?。
ここで敢えて「そんなこと」と言ったのは、
日常的には(2)と(5)の違いなんて大したことじゃないからです。
任意であろうと各であろうと、それは変化する不定な解集合を想定させます。
日常的には、それがわかれば十分です。数学的には大したことですが、
日常的にはそうでないことが原因で×を食らった学生(高校生を想定します)
の反応は次の3つだと思います。
① 数学は難しい。頑張ろう!(素直な人で、(1)と(3)の表現に慣れていく)。
② (2)と(5)の区別をちゃんと言え!(教師に嫌われるタイプで、 (3)の表現に会うと、何故か正しく解答し、各と任意の違いを朧気に意識している)。
③ 日常言語感覚が優先して、いくら説明されてもわからない (そのために(3)の表現に会っても、自信がないのでチンプンカンプンの解答を書く。 やってらんないので、数学を諦める)。
④ 注: いずれもステレオタイプです。
③タイプの人を見るたびに、大きなお世話ですが、なんか腹がたちます。
「そんなことのために」と思ってしまいます。
①タイプの人は、高校時代は順調でしょうが、受験突破後に数学から落伍するかもしれません。
(1)=(5),(2)=(3)という図式が体に染み付いたために
(数学の日常言語感覚になってしまったために)、
(2)と(5)の区別が、やはりできないからです。
大学では、(5)の言い回しもけっこう多用されると思います。
②タイプについては、①に昇格する可能性もありますし、③に向かう可能性もあります。
厳密に言うと(2)と(5)の違いは、(∀x)(∃y)と(∃y)(∀x)の順序交換問題です。
こんな話を高校生にするのは論外ですし、大学生にやってみたところで恐らく無視されます。
だから高校時代に、各何々表現さえやってもらえていれば、
(2)と(5)の違いは日常言語レベルで解決できたのにと思えるのです
(もう一回言いますが、現在の高校は知りません)。
問題文のほうも、それに合わせて欲しい。・・・以上、盛大な愚痴でした。

| NO.1246 | 2002.8.6. | おいたん | ホモセティックな関数(1) |
経済学では、ある企業が資本Kと労働Lを使用して物を生産するとき、
その生産量YがKとLの関数FでY = F(K, L)と与えられます。
この時、ホモセティックな関数というのが出てくるのですが、
それはtY = F(tK, tL)を満たす、すなわち、投入量をt倍したとき、
生産量も比例的にt倍になるという性質をもっています。
たとえばF(K, L)=KαL1-α…(1)はひとつの例です。
さて、このホモセティックな関数について質問があるのですが、
一般的に∂f/∂K>1であるとき、∂f/∂L<0となるのでしょうか。
上記(1)ではそうなりますが、
その他すべてのホモセティックな関数でもそうなのでしょうか。
どなたか証明を教えていただけませんか。

| NO.1247 | 2002.8.7. | BossF | ホモセティックな関数(2) |
おいたんさんによれば、homotheticとは、線形性みたいですが、
Homogeneous and homothetic technologies
によるとちょっとちがうみたいですね。
又、例に挙がってる
F(K,L)は F(K,L)=L・(K/L)α ですから、F(tK.tL)=F(K,L) になってしまうとおも
います。

| NO.1248 | 2002.8.13. | yokodon | 定積分(3) |
NO.1233の問2に関して、絶対誰かが思いついていそうな別解を投稿させて下さい。
求める積分の値を J とします。
t = exp(x) とおくと、dt/t = dx なので、
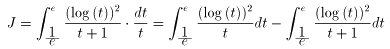
この右辺第2項で t = 1/s とおくと、dt = - ds/s2 であるから
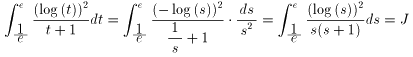
従って、
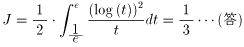

| NO.1249 | 2002.8.13. | yokodon | ホモセティックな関数(3) |
『ホモセティック(homothetic)』とは“相似の”“相似拡大的な”という意味で
、1次同次と事実上同じです。
例に挙がっていたような、F(x,y) = x1-a・ya は
F(tx,ty) = t・F(x,y) を
満たすので相似拡大的関数です。
他に、 F(tx,ty) = t・F(x,y) を満たす例として、
F(x,y) = px + qy (p, q は定数;これは1次関数ですね)
F(x,y) = f(x,y)/g(x,y) ;但し f(x,y) は n 次同次式に x または y をかけたも
の、g(x,y) は n 次同次式
…がありますね。
さて、問題の ∂F/∂x > 1 のとき ∂F/∂y < 0 が成り立つか否かですが、成り
立たない場合が存在します。
例えば、
F(x,y) = 2xy2/(x2 + y2)
を考えると(→上記第2例で、f = 2xy2 、g = x2 + y2 とおいた場合に相当)、
∂F/∂x = 2y2・(y2 - x2)/[(x2 + y2)2]
∂F/∂y = 4xy・(x2 - xy + y2)/[(x2 + y2)2]
で、例えば (x, y) = (1, 3) のとき、∂F/∂x =36/25 > 1 ですが ∂F/∂y > 0です。

| NO.1250 | 2002.8.13. | BossF | 断面が常に円である立体図形 |
みっちの隠れ家への投稿問題です。
立体図形の問題です。
ある閉曲面があり、その曲面が平面で切断されるときの断面が常に円であるとき、
この閉曲面は球であることを証明してください。

| NO.1250 | 2002.8.13. | 水の流れ | ネイピアの不等式 |
太郎さんは、数学Ⅲで、次のような不等式を扱ったことがあります。
先日、参考書を眺めていたら、この不等式が「ネイピアの不等式」
と呼ばれていることを知りました。
そこで、皆さんに、証明を次の3つの考え方で証明をしてください。
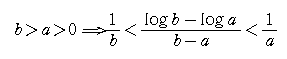
証明1:平均値の定理を用いて
証明2:微分を利用して
証明3:積分を利用して

 E-mail
E-mail
 戻る
戻る