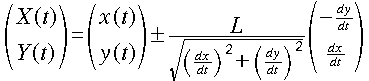
Weekend Mathematics/コロキウム室/NO.141
| NO.1201 | 2002.5.1. | yokodon | Bezier曲線の問題(2) |
Bezier 曲線C上の点を (x(t), y(t)) 、求める軌跡F上の点を (X,Y) とします。
「曲線と点の距離がLである」とは、「点から曲線上のある1点に下ろした垂線(線
分)の長さがLである」という意味であり、「曲線とある直線が直交する」とは、「
その直線と曲線の交点における曲線の接線を考えたとき、交点において接線と件の直
線が直交する」という意味であるとして考えます。
t を固定すると、C上の点 (x, y) における法線ベクトルは (-dy/dt, dx/dt) で
表せるので、(X, Y) としては以下のようにとればいいことになります。
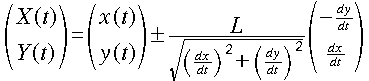
上式第2項が“太らせ”た部分になりましょうか。第2項が“±”になっているの
は、法線を伸ばす方向が平面上で2つあることによります(単位法線ベクトルの L
倍)。これを t の式に書き直しても、綺麗な形にはならなさそうですね。
想定している『距離』の取り方が違ってましたら、スミマセン。

| NO.1202 | 2002.5.1. | yokodon | 授業の担当クラス(2) |
まだ途中ですが、一応思いついた範囲で・・・。
問題1:n = 6 の場合
k = 1 のときは、{i} ;1 ≦ i ≦ 6 …の個数に等しく、F(6,1) = 6C1 = 6…(答)
k = 2 のときは、題意を満たすような {i,j};1 ≦ i < j ≦ 6 , j - i > 1
…の組の個数に等しく、
F(6,2) = 6C2 - 5 = 10 …(答)
k = 3 のときは、{1,3,5}、{1,3,6}、{1,4,6}、{2,4,6} しかなく、F(6,3) = 4…(答)
問題2:n = 7 の場合
k = 1,2 の場合は、それぞれ問題1と同様に考えて F(7,1) = 7、F(7,2) = 15…(答)
k = 3 の場合は、列挙すると
{1,3,5}、{1,3,6}、{1,3,7}、{1,4,6}、{1,4,7}、{1,5,7}、{2,4,6}、{2,4,7}、
{2,5,7}、{3,5,7}
で尽くされる。よって、F(7,3) = 10 …(答)
k = 4 の場合は、{1,3,5,7} しかなく、F(7,4) = 1 …(答)
問題3:n = 6, 7 の場合と同様に考えて、
F(n,1) = nC1 = n …(答)
F(n,2) = nC2 - (n -1) = 1/2・(n-1)(n-2) …(答)
きっと、ここまでは多くの方々がたどり着いておられるでしょう。
以下は、暫定の答で自信はないですが、とりあえず…。
問題5:n を1個増やしたときの F の増減を考える。
(i)1組から (n-1) 組までから k クラス選ぶ場合
このときの選び方の総数は、F(n-1, k) 通り。
(ii)1組から (n-1) 組までから (k-1) クラス選ぶ場合
このときの選び方の総数は、F(n-2, k-1) 通り。
なぜなら、n組と (n-1) 組とが隣り合う選び方は排除されるので、必然的に1組
から (n-2) 組までの中から (k-1) クラスを選ばなければならない。
上記の(i)(ii)は排反なので、F(n, k) で考えている場合はこの2つの場合の
和事象になる。
よって、以下が成り立つ。
F(n, k) = F(n-1, k) + F(n-2, k-1)
もうひとつ、つまんないかも知れませんが、以下も成り立ちますね。(^^;
F(n,2) = nC2 - F(n-1, 1)
いまのところ、ここまでです。(^^;

| NO.1203 | 2002.5.1. | 水の流れ | 正96角形(1) |
太郎さんが勤務している職場の先生から、
ある新聞の「余録」欄に掲載されて記事を紹介されました。引用します。
『「円周率は3.14でいいと思いますか、およそ3の方がいいと思いますか」
記者団に問われて、福田官房長官は「私だったらもっと言えますよ。3.14159265358とかね」
▲小数点以下11桁まですらすら言って 「早く計算するときもあるから考え方だと思います。 しかし、3は覚えられるけど、3.14は覚えられないというのはちょっとおかしいな」 と感想を付け加えた。
▲円周率は3.14を使うが、新指導要領に「目的に応じて3を用いてもよい」 とあるために混乱を招いた。円周率をπ(パイ)というのは周りや円周を意味するギリシャ語 ペリメトロンの最初の文字がπだからだ。 日本の教科書の円周率は普通まわりの3.14と大回りの3の二本立て
▲「アルキメデスの原理」で有名なアルキメデスは、円に内接する正6,12,24角形の周りを順々 に計算し、正48,96角形になったところで3.14163の円周率の近似値を出した。 紀元前3世紀で小数点以下3桁まで進んだのだから、 21世紀になってわざわざ3に退行することはない・・・』
この記事を読んで、アルキメデスが挑戦した正96角形の1辺を求めたくなりました。
勿論、三角関数の知識は未だ知りません。
だから、三平方の定理や無理数の存在は知っていたと思われます。
出来る限りアルキメデスが考えたと思う方法で考えてくだされば、幸いですが、
どんな考え方でも構いません。
ここでは、半径1の円に内接する正n角形の1辺の長さを求めることにします。
答えは無理数でお願いします。
問1.半径1の円に内接する正12角形の1辺の長さ
問2.半径1の円に内接する正24角形の1辺の長さ
問3.半径1の円に内接する正48角形の1辺の長さ
問4.半径1の円に内接する正96角形の1辺の長さ
さて、現在高校生は三角関数の極限lim(θ→0)sinθ/θ=1を習っています。
(ただし、θは弧度法)この定理を利用して、
問5.半径1の円に内接する正n角形の1辺の長さを三角関数を用いてnで表してください。
問6.半径1の円に内接する正n角形の周りを求めて、
半径1の円周をn→∞にしたときの極限として、求めてください。

| NO.1204 | 2002.5.1. | DDT | 空間上の円を動く2点 (2) |
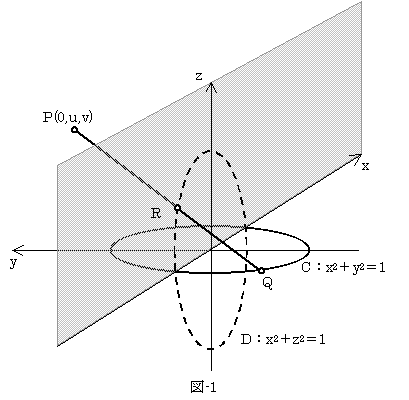
[状況調べ]
図-1に示すように、u>1>0より、Qが円C上の右側(y≦0)を動く時のみ、PQはxz平面とRで交わる。
またv>0では、PQとxz平面の交点Rは、xz平面の上半分のみに存在し、
v<0ではxz平面の下半分のみに存在する。
点Qが円Cの右側を動くとき、Qは必ずxz平面と(±1,0,0)でぶつかるので、Rの軌跡は必ず、
(±1,0,0)を通る。従って、点Rの描く軌跡が xz 平面上の円になるならば、
それは図-1にD:x2+z2=1として表した円Dの上半分(v>0の場合)か下半分(v<0の場合)となる。
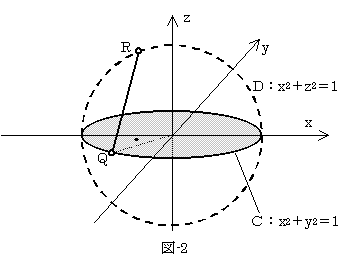
[Rを求める]
:角度パラメータα,方向はx軸から点線へ,0≦α≦π
Q=(-cosα,-sinα, 0 )
P=( 0 , u , v )
と書ける。QとPを通る直線の方程式は、
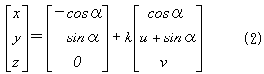
となるので(kは任意の実数)、PQとxz平面との交点Rは、(2)でy=0とおき、
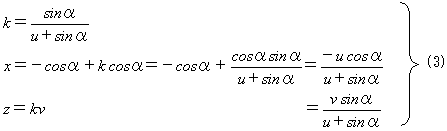
となる。図-1,2とu>1より、u+sinα≠0。(3)のR=(x,0,z)は、図-1,2の円D上にあるので、
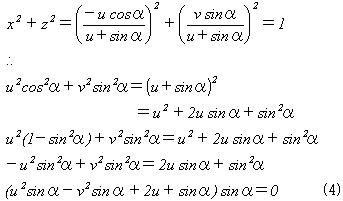
が得られる。
[(u,v)の条件を求める]
1.(4)でsinα≠0時
(4)でsinα≠0とすれば、
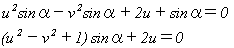 (5)
(5)
1−1.(5)でu2−v2+1≠0時
(5)でu2−v2+1≠0とすれば、
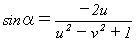 (6)
(6)
となる。(1)より0≦α≦πなので、0<sinα≦1とできる。従って(6)より、
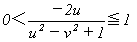 (7)
(7)
u2−v2+1>0とすれば、0<−2u≦u2−v2+1で、u<0が必要。u>1だったので不可。
u2−v2+1<0とすれば、u2−v2+1≦−2u<0で、u>0が必要かつ、
u2+2u+1−v2≦0
(u+1)2−v2≦0
(u+v+1)(u−v+1)≦0
で、u>1だったので(u>0を満たす)、

となる。
1−2.(5)でu2−v2+1=0の時
(5)でu2−v2+1=0とすれば、
2u=0でu=0
u>1だったので不可。
2.(4)でsinα=0時
(3)に戻れば、u≠0なのでx=±1,z=0となる。このとき(0,u,v)は明らかに任意。
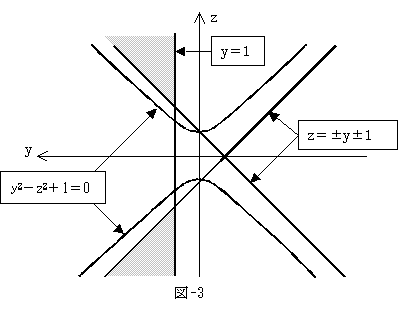 以上まとめれば、(u,v)の条件は、
以上まとめれば、(u,v)の条件は、

となるが、図-3より、
(u>1)かつ((v≧u+1)または(v≦−u−1)) (12)
でじゅうぶん。
No.1196は、特定のショートカットや、
ピンポイントのパターンや定理を知らなくても解けるという意味において、
非常に良問だと感じました。
ただ、ワードで絵を作ってたせいもありますが、
絵を仕上げて一応の解答にいたるまで4時間程かかりました。
模試や受験の数学の制限時間は2時間程度なので、実際には不合格です。
やはり受験は鍛えてないと駄目ですね。そういう意味で、
受験は訓練だという意見には賛成です。
ところでNo.1196のような難しい問題(と思いますが)さえ、
15分程度で解答を書き上げてしまうような努力の人は必ずいます。
しかしその人が、ショートカットやピンポイントのパターンも使わずにそんなことが
できるようになるまで鍛えているとすれば、恐らくその人は、数学(と物理)以外の
受験勉強は困難と思われます(個人的感想です)。
だからといって時間節約のために、ショートカットばかりを覚え込む受験訓練には賛成しかねます。
そんなことをすると、大学などに入ったのち、苦労します。
しかし、数学(と物理)しか鍛えていないと、他の語学などの科目で、その後やはり苦労します。
No.1196は恐らく、受験者100人の内60〜70人は正解にいたらない問題だと思います。
そこで、むかし看護予備校でバイトをしていたとき、「難しい問題には手をつけるな。
それより誰もが必ず解けるような問題を、必ず全問解け」とはっきり言ったことがあるのですが、
「生徒のやる気を殺ぐ」とお叱りを受け、そのまま首になりました。
受験は通ることが目的なのは否定できません。
また受験後苦労しないことも大事だと思います。
受験勉強には、上のような戦略的(?)配慮があっても良いような気がするのですが。
「生徒のやる気を殺ぐ」と言いながら、ピンポイントのショートカットばかりを
覚え込ませる看護予備校の体勢に納得できなかった、という愚痴でした。

| NO.1205 | 2002.5.1. | yokodon | 相加相乗平均不等式 |
一部修正 5/19 10:00
3月の問題で夜ふかしのつらいおじさんがお使いの“相加平均・相乗平均の不
等式”ですが(当時その解答を読んだときの驚きと言ったら!(^^; )、一般の場合
を示すことも割と簡単?に出来ます。僕が知っている方法は2つありますが、そのう
ちの一つをご紹介したいと思います。
まず、次の不等式を示します。
t > 0 に対して、tk - 1 ≧ k・(t - 1) ・・・[1]
(k:自然数)
[1] の証明ですが、
f(t) =([1] の左辺)-([1] の右辺)
とおいて微分を用いて示してもいいですし(t = 1 で極小値 0 をとり、且つこのと
き最小)、t と 1 の大小で場合分けして等比級数の公式を用いても可能です。
ここで、n 個の正の数 ai (i =1, 2, ..., n)に対して、以下のように置きます。
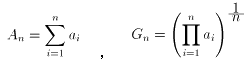
[1] 式で t = Gk/Gk-1 とおくと、
[Gk/Gk-1]k = ak/Gk-1 に注意して、
ak ≧ k・Gk - (k-1)・Gk-1 ・・・[2]
を得ます。等号は、Gk = Gk-1 のときのみ成り立ちます
(∵[1] の等号成立条件から)。
[2] に k = 2, 3, ..., n を代入して加えると、
a2 + a3 +...+ an = n・Gn - G1
ところで G1 = a1 ですから、あとは Gn と An の定義から、
1/n・An ≧ Gn
が成り立ちます。これが求める不等式です。
等号成立条件は、[2] で k = 2, 3, ..., n のときのそれであって、
Gn = Gn-1 = ... = G1
すなわち
an = an-1 = ... = a1
です。もう一つは、y = log(x) の凸性を用いるものですが、これはまた今度にさせて下さい。

| NO.1206 | 2002.5.1. | teki | できるだけ大きく! ・その後 |
1が4つの場合は1111、3が4つの場合は、
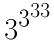 ですね。
ですね。
1の場合以外は、2つでの最大数をべき乗に使い、もう1つを底にして
超累乗を作ればいいわけですが、1の場合、話がややこしくなります。
結局、1111、1111の比較となりますが、後者の方がはるかに大き
いですね。

| NO.1207 | 2002.5.2. | 本多欣亮 | Bezier曲線の問題(3) |
yokodonさん、一般型の提示ありがとうございます。
題意はその通りで間違いありません。
実際のソフトウエア(Illustrator)では、かなり高い精度で“太ら
せた”図形を、別の複数の3次Bezier曲線で“近似”している様です
(しかも計算時間はかからず、殆ど瞬時に)。
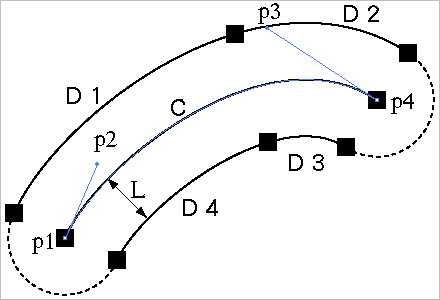
両端が半円弧(破線部)であることは題意から自明。
問題はそれ以外の部分で、この例ではIllustratorは4本の3次Bezier
曲線(D1〜D4)で“近似”している模様。
この近似曲線の構成法が具体的に判る方、いらっしゃいますか?
当方、Bezier曲線の形状を変えずに細分割する方法(こちらは厳密解)
などは、書籍を探し出して発見できたのですが、この問題のように
“(近似)オフセット”するアルゴリズムはいまだ観たことが
ありません。
もし、自由曲線や近似理論に詳しい方がおられましたら、引き続き
アイデアをお願いします。

| NO.1208 | 2002.5.4. | Junko | 正96角形(2) |
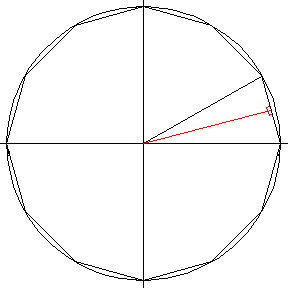
半径1の円に内接する正n角形の1辺の長さをL(n)とする。
問1
右の図より、半径1の円に内接する正12角形の1辺の長さL(12)は、
半角の公式 sin2(α/2)=(1−cosα)/2
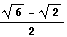
問2
同様に、L(24)=2sin(π/24)=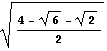
この値の概数をmathematicaで求め、πの近似値を出してみると、
π≒L(24)×12=3.13263
問3
同様に、L(48)=2sin(π/48)=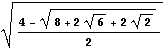
この値の概数をmathematicaで求め、πの近似値を出してみると、
π≒L(48)×24=3.13935
問4
同様に、L(96)=2sin(π/96)=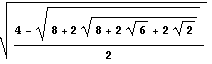
この値の概数をmathematicaで求め、πの近似値を出してみると、
π≒L(96)×48=3.14103
徐々にπの値に近づいていることがわかります。
問5
L(n)=2sin(π/n)
問6
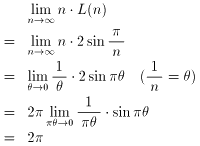
円周率πの値を内接多角形と外接多角形で近似シミュレーションできるサイトを紹介します。
THE UNIVERSITY OF UTAH の Archimedes and the Computation of Pi

| NO.1209 | 2002.5.5. | DDT | Bezier曲線の問題(4) |
No.1207でIllustratorが、4本の3次Bezier 曲線(D1〜D4)で、
"どのように"近似しているかの模様はわかりません。
もしIllustratorの正規ユーザーでいらっしゃるなら、
マニュアル付属の技術資料かオンラインのホワイトペーパーなどに書かれていないでしょうか?。
「自由曲線や近似理論に詳しい方がおられましたら、引き続きアイデアをお願いします(原文のまま)」
ですが、"詳しくない"のですが、じつは私はAutoCadユーザーです。
AutoCadは、いちおう世界一ユーザー数の多い製図道具と言われております。
拡張仕様を持たない素のAutoCadでは、自由曲線の拡幅(オフセット)を以下のように行います。
(1) まずAutoCadで自由曲線は、ポリラインから出発します(要するに折れ線です,図-1)。

(2)ポリラインを曲線化するには、ポリライン編集オプションのスプラインか、
フィットラインを用います。スプラインオプションはポリラインを、
図-1の折れ線の折れ点をコントロールポイントするスプラインに変えます。
このスプラインがBezier 曲線であったかどうかは自信ありません。
フィットラインも折れ点をコントロールポイントとして、最も滑らかにつながる円弧の集合にします。
図-2は、Wordのオートシェイプで書いた図なので、正確な再現ではありません。
(3)重要なのは素のAutoCadでは、図-2の自由曲線をオフセットしようとした場合、
そのままではできないという事実です。図-2の曲線をオフセットするには、
いったんスプラインまたはフィットラインオプションを解除して図-1のポリライン状態に戻し、
そこでオフセットします。オフセット後は図-3のようになり、
ポリラインを構成する直線セグメントのオフセットが交わらなければ延長して交点をつくり、
セグメントが交われば、そこでオフセットセグメントをトリムして、
図-4のオフセットポリラインをつくります。
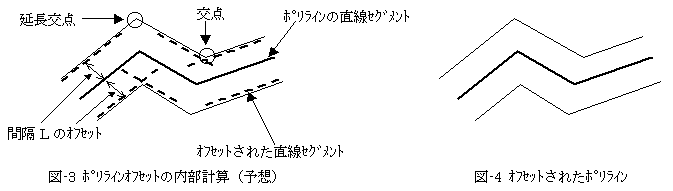
(4)結局、図-4の状態の3つのポリラインに曲線化オプションをかけて、
自由曲線の近似オフセットをつくります。

(5)いちおう世界一ユーザー数の多い製図道具と言われているAutoCadの虎の威を借りて言うと、
このような方法で得られた自由曲線の近似オフセットに不自由を感じたことはありませんし、
実用的だと思います。この方法は実質的に、
もとのBezier 曲線のコントロールポイントだけをオフセットして、
そこにBezier 曲線を引くだけですので、もしBezier 曲線を発生するアルゴリズムをお持ちなら、
そんなに難しい計算ではないと思います。もっとも研究目的などで高精度が必要なら、
明らかに精度不足です。

| NO.1210 | 2002.5.6. | 本多欣亮 | Bezier曲線の問題(5) |
DDTさん、回答ありがとうございます。
ちなみに私は正規ユーザーですが、Illustratorの場合、マニュアルには内部
処理までを詳しく述べた技術資料は付いていませんし、私が調べた範囲では
オフィシャルのプログラマ向けテックノートにもそのあたりのアルゴリズム
を解説したものは観たことがありません。

 E-mail
E-mail
 戻る
戻る