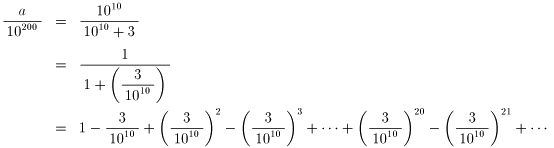
Weekend Mathematics/コロキウム室/NO.140
| NO.1193 | 2002.4.14. | Junko | 桁数は?(3) |
桁数がわかったところで後半、1の位の数を求めます。
a=10210/(1010 + 3)とします。
この数は200桁なので、10200でわれば、0.1以上1未満の数になります。
0.□□□・・・□・・・・・
その状態で小数第200位の数を求めればいいわけです。
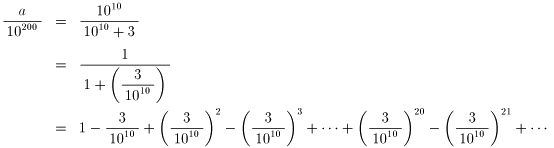
この変形は、
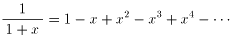 (|x|<1)
(|x|<1)
において、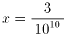 としたもにです。
としたもにです。
問題の小数第200位ですが、
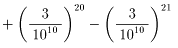 のあたりを見ていけばいいと思います。
のあたりを見ていけばいいと思います。
まず、(3/1010)20ですが、320の末尾は1になります。
従って、(3/1010)20だけを考えれば小数第200位の数は1です。
しかし、-(3/1010)21で若干引かれてしまうので、
小数第200位の数は「0」と結論しましたが・・・。

| NO.1194 | 2002.4.14. | yokodon | 桁数は?(4) |
321 の桁数(11桁)と1の位を用いて、 x21 と x20
のあたりから、ちょうどこの辺で1の位の評価が出来るというわけで、正解は9です
(∵ 321/1010 >1)。惜しい!ですね。

| NO.1195 | 2002.4.14. | Junko | 桁数は?(5) |
なるほど若干だと思ったらとんでもないのですね。
問題の仮定 321=10460353203 がここで生きてくるとは・・・!
小数第200位あたりの様子を書いてみました。
| 小数位 | ・・・ | 199 | 200 | 201 | 202 | ・・・ |
|---|---|---|---|---|---|---|
| (3/1010)20 | + | ・・・ | 1 | 0 | 0 | ・・・ |
| (3/1010)21 | - | 0 | 1 | 0 | 4 | ・・・ |
| a/10200 | + | ・・・ | 9 | ・・・ | ・・・ | ・・・ |

| NO.1196 | 2002.4.14. | yokodon | 空間上の円を動く2点 |
一部訂正 4/22、6:30
模試シリーズ10
xyz 空間において、xy 平面上の円C:x2 + y2 = 1, z = 0 と、
yz 平面上の点P(0, u, v) (u > 1, v ≠ 0)を与える。
更に、円Cの周上に点Qをとり、直線PQと xz 平面の交点をRとする。
点Qが円Cの周上を動くとき、点Rの描く軌跡が xz 平面上の円になったという。
u, v の満たすべき関係式を求めよ。

| NO.1197 | 2002.4.16. | yumi | 1周360度(1) |
なぜ,1周が360度なのか?
少しだけ書かれてあったのを見たのですが,
詳しく教えてくださいませんか?

| NO.1198 | 2002.4.16. | 授業の担当クラス |
太郎さんが勤務している高校のクラス数は、
1年生7クラス、2年生8クラス、3年生8クラスあります。
各クラスの授業時間割を編成するとき、なるべく
隣のクラスを同じ担当者が待たないほうが、経験上少し編成しやすいのです。
例えば、1学年5クラスのときを考えます。
太郎さんが1クラスだけ担当する場合は {1}、{2}、{3}、{4}、{5}
の5通りあります。
2クラス担当する場合は {1,3}、{1,4}、{1,5}、
{2,4}、{2,5}、{3,5}の6通り。
3クラス担当する場合は {1,3、5}の1通りしかありません。
ここで、問題です。
1学年1からnまでのクラスがあるとして、
この学年からk個のクラスを選んで授業担当をします。
ただし、時間割編成上隣り合わせのクラスは持たないとします。
そこで、このような持ち方の方法をF(n,k)通りとします。次の設問に答えてください。
問題1:n=6のとき、F(6,1)、F(6,2)、F(6,3)を求めよ。
問題2:n=7のとき、F(7,1)、F(7,2)、F(7,3)、F(7,4)を求めよ。
問題3:F(n,1)、F(n,2)をnで表せ。
問題4:F(n,k)をnとkで表せ。
問題5:何か漸化式みたいものが発見できたら、教えてください。

| NO.1199 | 2002.4.17. | Junko | 1周360度(2) |
蒸気機関車の問題のまとめで紹介しましたが、
暦と深い関係があるようです。
1周はなぜ360度なのか?
人類が農耕生活を始めた頃、自然の観察が必要であった。 季節があることに気づき、1年がほぼ360日であると考えるようになった。 この360日を円周上に配置したので、360度になったといわれている。
今日の度分秒の元祖はプトレマイオス(Ptolemaios)で、「アルマゲスト」は三角法の出発点である。
彼は円の半径を60にとり、これに等しい長さの弦のなす角を60度にした。
1年が360日であることと、プトレマイオスの考えがあいまって、1周が360度になったようである
(仙田章雄著、日本実業出版社、「数とグラフの雑学事典」より)

| NO.1200 | 2002.4.27. | 本多欣亮 | Bezier曲線の問題 |
Bezier曲線(ベジェ曲線)は、TrueTypeフォントやAdobe Illustrator等のソフト
で利用されている、コンピュータグラフィクスでお馴染みの曲線です。
平面上の3次Bezier曲線とは、以下の様に媒介変数表示できる有限長の曲線です:
任意の4点P1(x1,y1)、P2(x2,y2)、
P3(x3,y3)、P4(x4,y4)を与え、
x = t3 ・ x4 + 3・t2 ・ (1-t) ・ x3 + 3・t ・ (1-t)2 ・ x2 + (1-t)3 ・ x1
y = t3 ・ y4 + 3・t2 ・ (1-t) ・ y3 + 3・t ・ (1-t)2 ・ y2 + (1-t)3 ・ y1
(一部修正 03.11.5.)
0≦t≦1
そこで、問題です。
『互いに異なる任意の4点を与えた時、この4点で描いた3次Bezier曲線C までの距離が定数L>0である点が描く軌跡Fを求めて下さい』
『3次Bezier曲線CをL>0だけ太らせた図形Fを具体的に求めて下さい』
もちろんFをあらわす数式は1本でなく区分的で構いません。
あるいはFをあらわす近似式でも構いません。
難問だと思うので、部分的な解決でもあれば幸いです。
(補足)
Adobe Illustratorでは、F自身をBezier曲線であらわしています(「パスのオフ
セット」コマンド)。
が、これはたぶん近似でしょう。厳密にはF自身はBezier曲線ではあらわせない
と思います。

 E-mail
E-mail
 戻る
戻る