Weekend Mathematics乛栤戣乛栤戣63
俇俁丏懕丒偳偪傜偑戝偒偄丠
俆侽俋俋偲俋俋両偱偼偳偪傜偑戝偒偄偱偟傚偆偐丠
拲乯俋俋両偵偮偄偰
悢妛偺傂傠偽
僪儈僩儕丒僼僅儈乕儞丄僙儖僎僀丒僎儞僉儞丄僀儕儎丒僀僥儞儀儖僋挊
巙夑峗擇丄揷拞婭巕栿
娾攇彂揦
乮儁儞僱亅儉丗傗側偣乯
俋俋両傛傝俆俆偺俋俋忔偺曽偑偐側傝偱偐偄
懘張傑偱偺偐偰偄
傑偢丄僄僋僙儖傪棫偪忋偘傑偡乮傕偆偙傟偱丄偁偒傟偨偐側丠乯
揔摉側僙儖偵亖俥俙俠俿乮俋俋乯偲擖椡偟偰俤値倲倕倰
偡傞偲丂9.3326E+155偲偱傑偡丅
師偵堘偆僙儖偵亖俆侽俋俋偲擖椡偟偰俤値倲倕倰
偙傟傑偨丂1.5777E+168
偲弌偰偒傑偟偨丅
偙傟偼傕偆柧傜偐偵寘悢偑堘偆偺偱楌慠偱偡偹丅乮敋徫乯
擮偺偨傔偵丄僙儖偺彂幃傪悢抣偵愝掕偡傞偲惁偄偙偲偵側偭偰偟傑偄傑偟偨丅
偄傗偀乣懠偺奆偝傫傒偨偄偵丄偒偪傫偲弌棃傑偣傫偑
嵟嬤偼曋棙側暔偑偁傞偺偱偲偵偐偔摎偊偩偗偼弌傑偡偹丅

乮儁儞僱亅儉丗僗儌乕僋儅儞乯
| 99両 | =乮50+49乯乮50+48乯丒丒丒乮50-48乯乮50-49乯 |
| =乮502-492乯乮502-482乯丒丒 乮502-12乯50 | |
| =5099-5097乮12+22+丒丒丒+492乯 +5095乮12*22+丒丒丒+482*492乯 -5091乮12*22*32*+丒丒丒+472*482*492乯 | |
| 丂丂丂+丒丒丒-50*12*22*丒丒丒*492 |

乮儁儞僱亅儉丗QPer乯
掙50乮亜1) 偺懳悢傪偲傞丅偙偙偱偼掙偼徣棯偟傑偡丅
log5099=99
| log99! | =log99+log98+乧+log1 |
| =log99*1+log98*2+乧+log51*49+log50 |
| log99! | 亙log502+log502+乧+log502+log50 |
| =2+2+乧+2+1 | |
| =2*49+1 | |
| =99 |

乮儁儞僱亅儉丗僗僠儏乕僨儞僩乯
| 俋俋両 | |
| 亖 | 俋俋丒俋俉丒俋俈丒丒丒俆侾丒俆侽丒係俋丒丒丒俁丒俀丒侾 |
| 亖 | 乷乮俋俋丒侾乯乧嘆乸亊乷乮俋俉丒俀乯乧嘇乸亊乷乮俋俈丒俁乯乧嘊乸亊丒丒丒乷俆侾丒係俋乧係俋崁栚乸丒俆侽 |
| 俆侽俋俋 | |
| 亖 | 乮俆侽丒俆侽乯丒乮俆侽丒俆侽乯丒乮俆侽丒俆侽乯丒丒丒乮俆侽丒俆侽乯 |
| 亖 | 乮俆侽丒俆侽乧嘆乫乯丒乮俆侽丒俆侽乧嘇乫乯丒乮俆侽丒俆侽乧嘊乫乯丒丒丒乮俆侽丒俆侽乧係俋崁栚乫乯丒俆侽 |
嘆偲嘆乫丄嘇偲嘇乫丄嘊偲嘊乫丄丒丒丒係俋崁栚偲係俋崁栚乫傪偦傟偧傟斾妑偡傞偲丄
丂俋俋丒侾亙俆侽俀
丂俋俉丒俀亙俆侽俀
丂俋俈丒俁亙俆侽俀
丂丂丂丂丂丒
丂丂丂丂丂丒
丂俆侾丒係俋亙俆侽俀
傑偨丄俆侽崁栚偼
丂俆侽亖俆侽
奺崁偼慡偰亄偱偁傞偺偱丄俆侽俋俋偺曽偑戝偒偄丅

乮儁儞僱亅儉丗偙偞偭傁乯
| 99! | = 99*98*97*96*丒丒丒丒4*3*2*1 | 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
| = 50*(51*49)*(52*48)*(53*47)*丒丒丒丒(96*4)*(97*3)*(98*2)*(99*1) | <- 50傪偼偝傫偱嵍塃偺悢帤偑慻偵側傞傛偆偵暲傃懼偊偨 | |
| = 50{(50+1)(50-1)}{(50+2)(50-2)}{(50+3)(50-3)}丒丒丒丒{(50+48)(50-48)}{(50+49)(50-49)} | <-奺悢帤傪50偲悢抣偺壛尭嶼偱昞尰偱偒傞傛偆偵偟偨 | |
| = 50{502-12}{502-22}{502-32}{502-42}丒丒丒丒}{502-482}{502-492} | <- (X+C)(X-C)=X2-C2傪棙梡偟偰幃傪曄宍 |
堦曽丄5099偼丄
5099= 50*(50*50)(50*50)(50*50)*丒丒丒丒(50*50)(50*50)
偲側傝丄50偑1屄偲丄502偑49屄偺忔嶼偲峫偊傜傟傞丅 丂丂丂丂丂丂丂丂丂丂丂丂 丒丒丒丒嘇
嘆偲嘇傪斾妑偡傞丅 偄偢傟傕50屄偺悢帤偺忔嶼偱丄偦偺偆偪1屄偼50偱摨偠偩偑丄偦傟埲奜偺懠偺49屄偺悢帤偼偡傋偰 k2偺暘偩偗99!偺曽偑彮側偄丅乮k偼1乣49乯 偐偗傞悢帤偺屄悢偑摨偠偱丄偦偺悢帤偑侾屄(50)傪彍偒丄偡傋偰彫偝偄偺偩偐傜丂5099丂>丂99!偲側傝傑偡丅
Ans丂5099偺曽偑戝偒偄丅

乮儁儞僱亅儉丗偲偟乯
俆侽俋俋偑戝偒偄丅
乮侾侽侽亅N乯N亖亅乮N亅俆侽乯俀亄俆侽俀

乮儁儞僱亅儉丗kiyo乯
俀*俋俋亙俆侽*俆侽
俁*俋俉亙俆侽*俆侽
.....................................
係俉*俆侾亙俆侽*俆侽
係俋*俆侽亙俆侽*俆侽
偱偁傞偐傜丄
俋俋両亙乮俆侽*俆侽乯係俋亖俆侽俋俉亙俆侽俋俋
俆侽俋俋偺曽偑戝偒偄丅

乮儁儞僱亅儉丗俶偲乣乯
俆侽俋俋亜俋俋両
| 俋俋両 | 亖俋俋丒俋俉丒俋俈丒丒丒丒丒俆俀丒俆侾丒俆侽丒係俋丒係俉丒丒丒丒丒俁丒俀丒侾 |
| 亖乮俋俋丒侾乯丒乮俋俉丒俀乯丒乮俋俈丒俁乯丒丒丒丒丒乮俆俀丒係俉乯丒乮俆侾丒係俋乯丒俆侽 |
| 俋俋丒侾 | 亙俆侽丒俆侽 |
| 俋俉丒俀 | 亙俆侽丒俆侽 |
| 俋俈丒俁 | 亙俆侽丒俆侽 |
| 丒丒丒丒丒丒 | |
| 俆俀丒係俉 | 亙俆侽丒俆侽 |
| 俆侾丒係俋 | 亙俆侽丒俆侽 |
| 俆侽 | 亖俆侽 |

乮儁儞僱亅儉丗奰杮丂峗乯
| 俋俋両 | 亖侾亊俀亊丒丒丒亊係俋亊俆侽亊俆侾亊丒丒丒亊俋俉亊俋俋 |
| 亖乮俆侽亅係俋乯亊乮俆侽亅係俉乯亊丒丒丒亊乮俆侽亅侾乯亊俆侽亊乮俆侽亄 侾乯亊丒丒丒亊乮俆侽亄係俉乯亊乮俆侽亄係俋乯 |
| 俋俋両 | 亖俆侽亊乷乮俆侽亅侾乯亊乮俆侽亄侾乯乸亊乷乮俆侽亅俀乯亊乮俆侽亄俀乯乸 |
| 丂丂丂亊丒丒丒乷乮俆侽亅係俉乯亊乮俆侽亄係俉乯乸亊乷乮俆侽亅係俋乯亊乮俆侽亄係俋乯乸丂丗幃侾 |
乮俆侽亅侾乯亊乮俆侽亄侾乯亖俆侽俀亅侾俀
乮俆侽亅俀乯亊乮俆侽亄俀乯亖俆侽俀亅俀俀
丂丂丂丒
丂丂丂丒
丂丂丂丒
乮俆侽亅係俉乯亊乮俆侽亄係俉乯亖俆侽俀亅係俉俀
乮俆侽亅係俋乯亊乮俆侽亄係俋乯亖俆侽俀亅係俋俀
偱偁傝丄幃侾偺乷丂乸偱妵傜傟偨拞偺愊偼丄慡偰俆侽俀傛傝彫偝偄帠偑暘偐傞丅
俆侽俀傛傝彫偝偄帺慠悢傪係俋屄忔嶼偟偨愊傛傝傕
俆侽俀傪係俋屄忔嶼偟偨愊丄偡側傢偪俆侽俋俉偺曽偑戝偒偄帠偼柧敀偱偁傝
乮俆侽俀亅侾俀乯亊乮俆侽俀亅俀俀乯亊丒丒丒亊乮俆侽俀亅係俉俀乯亊
乮俆侽俀亅係俋俀乯亙俆侽俋俉
椉曈偵俆侽傪偐偗偰
俆侽亊乮俆侽俀亅侾俀乯亊乮俆侽俀亅俀俀乯亊丒丒丒亊乮俆侽俀亅係俉俀乯
亊乮俆侽俀亅係俋俀乯亙俆侽亊俆侽俋俉
丂丂丂丂丂丂丂丂伀
俆侽亊乮俆侽亅侾乯亊乮俆侽亄侾乯亊乮俆侽亅俀乯亊乮俆侽亄俀乯亊丒丒丒乮俆侽亅
係俉乯亊乮俆侽亄係俉乯亊乮俆侽亅係俋乯亊乮俆侽亄係俋乯亙俆侽俋俋
丂丂亪俋俋両亙俆侽俋俋

乮儁儞僱亅儉丗儌儖儌僢僩戝恇乯
戣堄傛傝99!/5099傪媮傔偰偙傟偑1傛傝戝偒偄偐偳偆偐偱戝彫偺敾掕傪偟傑偡丅
丂丂99!/5099=(99亊98亊97 亊丒丒丒3亊2亊1)/(50亊50 亊丒丒丒50亊50)
暘巕暘曣偲傕偦傟偧傟99崁偱偡丅(崁偲偄偆偺偼壗偐曄偱偡偑偍嫋偟傪)
偝傜偵偙偺幃傪曄宍偟偰
丂丂99!/5099=99/50亊98/50亊丒丒52/50亊51/50亊50/50亊49/50亊48/50丒丒2/50亊1/50
慡晹偱99崁
偙偙偱50/50偺嵍塃偺49崁偢偮傪傛偔尒偰傒傞偲
丂丂丒丒52/50亊51/50亊50/50亊49/50亊48/50丒丒偱偁傝(50亇1,2,3丒丒49)/50
偺娭學偲側偭偰偄傞丅偦偙偱偙偺 亇偺屻偺悢帤偑摍偟偄崁偺愊傪峫偊傞丅傛偭偰
丂丂99!/5099=50/50亊(502-12)/502 亊(502-22)/502 亊(502-32)/502
丒丒丒丒(502-482)/502 亊(502-492)/502丂
丂丂丂丂乮慡晹偱49+1崁乯
偙偙偱偦傟偧傟偺崁偼 (502-N2)/502 (N偼1乣49傑偱偺惍悢)偱偁傝
(502-N2)/502 =1-(N/50)2亙1偱偁傞偨傔丄
99!/5099=1亊[1-(1/50)2]亊[1-(2/50)2]亊[1-(3/50)2]丒丒[1-(48/50)2]亊[1-
(49/50)2]偺愊偼慡偰1埲壓偺49崁偺愊偲側傞偐傜1埲壓偱偁傞丅
偟偨偑偭偰 99!/5099亙1偩偐傜 99!亙5099偲側傝徹柧廔傢傝丅

乮儁儞僱亅儉丗teki乯
摎偊丂丂俆侽99亜俋俋両
亙夝朄亜
乽僈僂僗偺懌偟嶼乿側傜偸乽僈僂僗偺偐偗嶼乿偱峫偊傑偟偨丅
偮傑傝丄
| 俋俋両 | 亖乮1亊99乯亊乮2亊98乯亊丒丒丒丒丒亊乮49亊51乯亊50 |
| 俆侽99 | 亖乮50亊50乯亊乮50亊50乯亊丒丒丒丒丒亊乮50亊50乯亊50 |

乮儁儞僱亅儉丗崅嫶 摴峀乯
摎偊5099偺曽偑戝偒偄
崱夞偺栤戣偼慜夞偲摨偠傛偆偵偲偒傑偟偨丅(偳偙偑摨偠偐偼晄柧)
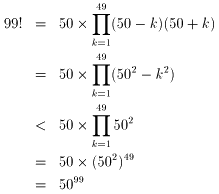
傛偭偰5099偺曽偑戝偒偄

乮儁儞僱亅儉丗俛倧倱倱俥乯
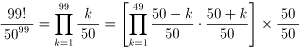
偲偙傠偑丄侾亝k亝49偱
(50-k)/50丒(50+k)/50=(502-k2)/502亙1
偩偐傜
99!/5099亙1丂i.e. 99!亙5099
傁偭偲尒偨帪偺梊憐偲媡偵側偭偰價僢僋儕偟傑偟偨丅

乮儁儞僱亅儉丗Wasmath乯
偝偰丆栤戣俇俁偱偡偑丆堦斒壔偟偰
n偑俀埲忋偺帺慠悢偺偲偒 n2n-1亜(2n-1) !
丂丂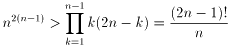
亪 n2n-1亜(2n-1) !

乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
夝摎侾
侾偐傜俋俋傑偱偺帺慠悢偵偮偄偰憡壛暯嬒偲憡忔暯嬒偺娭學傪梡偄傞偲丄
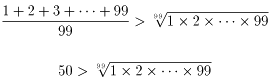
椉曈傪俋俋忔偟偰丄
丂丂俆侽俋俋亜侾亊俀亊丒丒丒亊俋俋
傛偭偰丄俆侽俋俋亜俋俋両
夝摎俀
| 俋俋両 | 亖俋俋亊俋俉亊丒丒丒亊俆侾亊俆侽亊係俋亊丒丒丒亊俀亊侾 |
| 亖乮俋俋亊侾乯亊乮俋俉亊俀乯亊丒丒丒亊乮俆侾亊係俋乯亊俆侽 | |
| 亖乮俆侽亄係俋乯亊乮俆侽亅係俋乯亊乮俆侽亄係俉乯亊乮俆侽亅係俉乯亊丒丒丒亊乮俆侽亄侾乯亊乮俆侽亅侾乯亊俆侽 | |
| 亖乮俆侽俀乕係俋俀乯亊乮俆侽俀乕係俉俀乯亊丒丒丒亊乮俆侽俀乕侾俀乯亊俆侽 | |
| 亙俆侽俀亊俆侽俀亊丒丒丒亊俆侽俀亊俆侽 | |
| 亖俆侽俋俋 |
夝摎俁
| log10俆侽俋俋 | 亖俋俋log10(俆亊侾侽) |
| 亖俋俋(log10俆亄log10侾侽) | |
| 佮俋俋(侽丏俇俋俋亄侾) | |
| 亖俋俋亊侾丏俇俋俋 | |
| 亖侾俇俉丏俀侽侾 |
| log10(俋俋両) | 亖log10(侾亊俀亊丒丒丒亊俋俋) |
| 亖log10侾亄log10俀亄丒丒丒亄log10俋俋 |
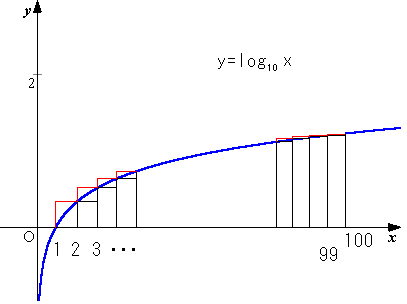
塃恾傛傝丄愒偄挿曽宍偲僌儔僼傛傝
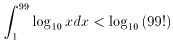
崟偄挿曽宍偲僌儔僼傛傝
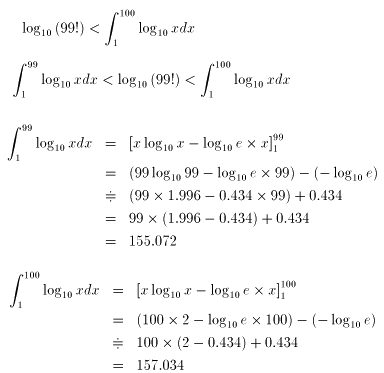
廬偭偰丄俋俋両偼侾俆俇寘偐傜侾俆俉寘偺悢
傛偭偰丄俆侽俋俋亜俋俋両

乮儁儞僱亅儉丗俰倳値倐倧倳乯


乮儁儞僱亅儉丗yokodon乯
寁嶼婡偱傗傟偽傾僢偲偄偆娫偱偡偑丄偦傟偱偼僫儞側偺偱丄悢妛偺栤戣傜偟偄媍榑
傪偟偰傒偨偄偲巚偄傑偡丅偨偩丄埲壓傪婛抦偵偟偨偄偲巚偄傑偡丅側偍丄 log(x) 偼
忢梡懳悢傪丄ln(x) 偼帺慠懳悢傪昞偡偙偲偵偟傑偡丅
log1.25 佮 0.097 偍傛傃 e 亜 2.5
y 亖 ln(x) 偺僌儔僼傪峫偊傞偲丄埲壓偺晄摍幃傪梕堈偵帵偡偙偲偑弌棃傑偡丅
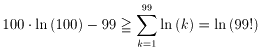
偙偺椉曈傪 ln10 偱妱傞偲丄埲壓偺傛偆偵側傝傑偡丅
200 - 99丒log(e) 亞 log(99!)丂丒丒丒[1]
偝偰丄log(5099) 亖 198 - 99丒log2 偱偡偐傜丄
| (198 - 99丒log2) - (200 - 99丒log(e)) | |
| 亖 | 99丒log(e/2) - 2 |
| 亜 | 99丒log(2.5/2) - 2 |
| 亜 | 99丒0.095 - 2 |
| 亖 | 7.405 亜 0丂丒丒丒[2] |
場傒偵丄寁嶼婡偱傗偭偰傒傞偲丄
丂丂log(5099) 佮 168.198...
丂丂log(99!) 佮 155.970...
側偺偱丄捈偪偵尵偊傑偡丅
#懳悢偺抣傪慜採偵偟側偄忋庤偄夞摎傪丄扤偐偒偭偲偟偰偄傞傫偩傠偆側偀丅
##懳悢傪巊傢側偄媍榑傕丄扤偐偟偰偄偦偆偩側偀丅

乮儁儞僱亅儉丗寧偺岝乯
[妱傞曽朄]
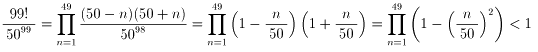
傛偭偰99!<5099
[僗僞乕儕儞僌偺岞幃]
99!佮(99/e)99<5099偱偡丅
n!佮(n/e)n偑僗僞乕儕儞僌偺岞幃偐傜暘偐傝傑偡丅乮n偑戝偒偄偲偒乯

| kiyo | teki | 崅嫶 摴峀 |
| 儌儖儌僢僩戝恇 | 僗僠儏乕僨儞僩 | 偙偞偭傁 |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | 偲偟 | 俰倳値倐倧倳 |
| Wasmath | 俛倧倱倱俥 | 傗側偣 |
| yokodon | QPer | 僗儌乕僋儅儞 |
| 俶偲乣 | 奰杮丂峗 | 寧偺岝 |

傗側偣偝傫偐傜夝摎傪偄偨偩偒丄偝偭偦偔巹傕Excel偱傗偭偰傒傑偟偨丅 偄傗偁丄偡偛偄丅偙傫側偵寘悢偺戝偒偄寁嶼傪傗偭偰偔傟傞偲偼巚偭偰傕傒傑偣傫偱偟偨丅 巹偼偙偺栤戣丄専徹偼偱偒側偄偩傠偆偲巚偭偰偄傑偟偨偑丄偱偒傑偡偹丅
崱夞婑偣傜傟偨夝摎偼丄teki偝傫偺僱乕儈儞僌偵傛傞乽僈僂僗偺偐偗嶼乿晽曄宍傪梡偄偨夝摎偲丄 寘悢偱斾妑偡傞夝朄偵戝偒偔暘偗傜傟傞偐側偲巚偄傑偡丅
巹帺恎偼丄慜幰偺僷僞乕儞偱乽憡壛丒憡忔暯嬒乿偺娭學傪巚偄晜偐傋傑偟偨丅
偮傑傝丄
丂丂丂丂乽憡壛丒憡忔暯嬒乿偺娭學
倎丆倐亜侽偱偁傞偲偒丄師偺晄摍幃偑惉傝棫偮丅
丂丂丂丂丂丂
偨偩偟丄摍崋偑惉棫偡傞偺偼丄倎亖倐偺帪偵尷傞丅
俋俋両 亖乮1亊99乯亊乮2亊98乯亊丒丒丒丒丒亊乮49亊51乯亊50 俆侽99 亖乮50亊50乯亊乮50亊50乯亊丒丒丒丒丒亊乮50亊50乯亊50
偵偍偄偰丄乽憡壛丒憡忔暯嬒乿偺娭學傪梡偄傞偲
偮傑傝丄teki偝傫棳偵尵偆偲丄堦掕偺挿偝偺傂傕偱挿曽宍傪嶌傞偲偒丄偦偺柺愊偑 嵟戝偵側傞偺偼惓曽宍偺応崌偱偁傞偲偄偆偙偲偱偡丅
偱偡偐傜丄屻幰俆侽99偺曽偑戝偒偄偲偄偆傢偗偱偡丅
尩枾偵尵偊偽丄俋俋屄偺惓悢偵懳偡傞乽憡壛丒憡忔暯嬒乿偺娭學傪 徹柧偟側偗傟偽側傜側偄偲偼巚偄傑偡偑丄 栭傆偐偟偺偮傜偄偍偠偝傫 偺夝摎侾傕偍傒偛偲偱偡偹丅
偝偰丄偙偺栤戣偵娭楢偟偰丄
Wasmath偝傫(NO.1183丂懕乆丒偳偪傜偑戝偒偄丠)偲
yokodon偝傫(NO.1184丂寘悢偼丠)偐傜敪揥揑側栤戣傪偄偨偩偒傑偟偨丅
僐儘僉僂儉幒偺曽偵嵹偣偰偍偒傑偟偨丅 偙傟偵偮偄偰偺搳峞傕偍懸偪偟偰偄傑偡丅
栠傞
top