同じ数字を３個使って、できるだけ大きい数を表すにはどうしたらいいか。
９が３個の場合は、
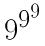
という具合に配置し、いわば９の「超累乗」をつくればよい。
この数はとてつもなく大きくて説明しようにも比べるものがないほどである。
さて問題、
計算記号を使わないで数字の２だけを３つ使って、できるだけ大きい数を表すにはどうしたらよいか。
Weekend Mathematics／問題／問題64
６４．できるだけ大きく！
同じ数字を３個使って、できるだけ大きい数を表すにはどうしたらいいか。 ９が３個の場合は、
という具合に配置し、いわば９の「超累乗」をつくればよい。 この数はとてつもなく大きくて説明しようにも比べるものがないほどである。 さて問題、
計算記号を使わないで数字の２だけを３つ使って、できるだけ大きい数を表すにはどうしたらよいか。
おもしろい数学教室
ペレリマン著
山崎昇訳
東京図書
（ペンネ−ム：ガリ勉）
考えたんですが、またまた直感です（？？）
２２２
なんてどうでしょうか？
今のところ一番大きい数です。
（ペンネ−ム：ドラ）
２２２＝２・２・２・・・・・・２・２・２＝４１９４３０４
（ペンネ−ム：QPer）
２２２と２２２と２２２と２の超累乗くらいしか思いつかないんですよね。
２２２＝４８４
２２２＝４１９４３０４
２の超累乗は１６だから 答えは ２２２でしょうか？
（ペンネ−ム：スチューデント）
考えられる数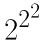
、２２２、２２２、２２２を比べて、
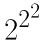＝２４であるので、
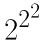＜２２２
２２２＝２５×２５×２１２＝３２２×２１２であるので、２２２＞
２２２ （３２２＞２２２）
２２２＝２８×２１４＝２５６×２１４であるので、 ２２２＞２２２
｛２５６×ｎ＞２２２（ｎは１以上）｝
以上の結果から、２２２が一番大きい。よって、２の２２乗。
（ペンネ−ム：こざっぱ）
「計算記号」とはどの範囲まで入っているのでしょうか。
三角関数や対数、極限、Σ、積分などはすべて計算記号に入ると思ってよいですか。
と、いうことは、数字以外はなーんにも使ってはいけないのでしょうか。。。
累乗だけで考えてみますと、感覚的に思ったのとは違って、
２２２＝４１９４３０４
が一番大きいと思います。
（ペンネ−ム：kiyo）
解答は、
２２２＝４１９４３０４
（ペンネ−ム：モルモット大臣）
数学記号を使わず、2を3個使用して最大数を作るには数学パズルの問題的発想ではこ
れしか思いつきません。
答えは222が最大です。
（ペンネ−ム：高橋 道広）
答え ２22
この問題の理論はありません。勘です。
（ペンネ−ム：ＢｏｓｓＦ）
計算記号を使わないで…となると
222、 222、 222、
（ペンネ−ム：yokodon）
かっこや小数点、分数表記や階乗なども全く使わないとすると、数字の２を３個だ
け使って表せる数字は、以下の４つくらいしか思いつかないです。
222
222（＝ 484）
222（＝ 4194304）
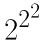（＝ 16）
このうち、最大なのは 222 です。…(答)
（ペンネ−ム：夜ふかしのつらいおじさん）
計算記号を使わないで数字の２だけを３つ使って数をつくる。
このとき、もともとある２に対して次の２は、下のどちらかの方法で付け加える。
ａ）小さくして右上につなげる（べき乗）
ｂ）同じ大きさで右につなげる（１桁増）
（１）
＝２４＝１６
（２）２２２＝２（１０＋１０＋２）＝２１０×２１０×２２＝１０２４×１０２４×４＝４１９４３０４
（３）２２２＝４８４
（４）２２２
（ペンネ−ム：月の光）
222=4194304が考えた数の中で今の所もっとも大きな数です。
大きな数といえばスキューズ数やギネスブックにも載っているグラハム数というのがあるそうで
す。
スキューズ数はコロキウム室NO.519
「D(n)＝π(n)− ｌｉ(n)は常に増加するように見えますが、１９１４年、ジョン・リトルウッ ドは D(n)は十分大きなｎに対して減少するだけでなく、負になり、正と負の間の符号を無限回 変えることを証明しました。」
（ペンネ−ム：スモークマン）
2の22乗。
3までは、3の3乗＜33だけれど、4以上は明らかに、4の4乗＞44
となる。
（ペンネ−ム：teki）
答え ２22（４１９４３０４）
この問題、私も考えたことがあります。
１が３つの場合は、１１１、２及び３が３つの場合は、２22及び３33、
４以上は、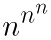
となります。
考え方としては、まず２つで最大となるものを考え、これをべき乗に
使うのですが、１の場合は、元が１ですので、１１１が最大となります。
| kiyo | teki | スモークマン |
| QPer | ＢｏｓｓＦ | 夜ふかしのつらいおじさん |
| こざっぱ | スチューデント | 高橋 道広 |
| ガリ勉 | ドラ | yokodon |
| モルモット大臣 | 月の光 |
『「計算記号」とはどの範囲まで入っているのでしょうか。 三角関数や対数、極限、Σ、積分などはすべて計算記号に入ると思ってよいですか。 と、いうことは、数字以外はなーんにも使ってはいけないのでしょうか。。。』
というような質問をいくつか受けました。 数学ですからことばの定義は重要ですよね、反省。 私自身は上記のような解釈をしました。 数字３つをただ単に配置しただけで、どれだけ大きい数を表現できるか？ という問題のつもりです。
例に示したように、「超累乗」が一番大きいと思いがちですが、「２」の場合は違います。
たかだか
それに比べて、２２２＝４，１９４，３０４ですからね。
思いこみは危険で、きちんと検証しなければならないという例だと思います。
tekiさんがまとめをしてくださいましたが、 １の場合は「１１１」がもっとも大きい数、２〜３については、「ｎｎｎ」がもっとも大きく、 ４以上については、超累乗ｎｎｎ、つまりｎ１１ｎと
ｎｎ−１１ｎ＝ｎ(ｎｎ−１−１１)
となります。４以上のｎについて、ｎｎ−１−１１＞０となりますから、 上記の結果になることがわかります。
さて、この問題を発展させて数字の数を４つとしたらどうでしょう？
夜ふかしのつらいおじさんの解答にもありますが、この場合は８通りが考えられます。
２２２２、２２２２、２２２２、２２２２
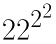
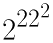
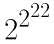
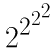
底で分類してみます。
- ２２２２
- ２２２２＝４９，２８４
従って候補となるのは、２２２２と、
となり、圧倒的な差があることがわかります。
従って、４つの２を配置してできる最大の数は、
４つの１、４つの３・・・と考えてみてください。 案外、予想に反した結果がでると思います。
関連して → コロキウム室NO.1206
E-mail
戻る
top