Weekend Mathematics/コロキウム室/NO.128
| NO.1089 | 2001.11.10. | 水の流れ | あみだくじ(4) |
|
|
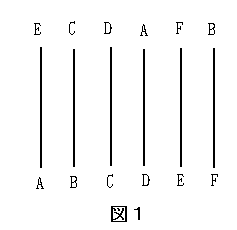
図のような あみだくじを作りました。
AがAに、BがBに、CがCに、DがDに、EがEに、FがFにいくように
横線を最低何本引いたらいいでしょう。実際に引いてください。
(横線の引き方の順序はいろいろあると思われます)
最低、何本必要かその考え方を教えてください。

| NO.1090 | 2001.11.13. | yokodon | 動く楕円(1) |
模試シリーズ7
xyz 空間に、直線 l :y = 0 , z = 2 と、平面π:z = 1 がある。
3点P、Q、Rはそれぞれ直線 l 、平面π、xy 平面上にあり、またこの3点は同
一直線上にあるものとする。
更に線分PRの長さは 2√2 で、点Qの x 座標 q は、
-1 ≦ q ≦ 1 を満たすものとする。
点Rの存在しうる範囲を、xy 平面上に図示せよ。

| NO.1091 | 2001.11.16. | 水の流れ | 正(2n+1)角形(1) |
今、太郎さんは学校で理系の生徒に積分法を、
文系の生徒には複素数平面を教えようとしています。
過去の大学入試問題を眺めていたら、弘前大学で次のような問題がありました。
興味深い事実に感嘆しながらご紹介します。
問題1:
複素数平面上の原点Oを中心とする半径1の円周上に、
複素数 α,β,γ,δがこの順に並んでいる。
α,β,γ,δでできている四角形の対角線が直交する条件は、
αγ+βδ=0 であることを証明せよ。
問題2:
原点を中心とし、半径1の円周上に頂点をもつ正(2n+1)角形(nは自然数)の対角線は、
どれも直交しないことを証明せよ。

| NO.1092 | 2001.11.16. | truth | 三角形可能な確率(3) |
「Introduction-to-Probability」という本にNO.450(99年4月25日出
題)三角形可能な確率(1)と同じ問題がのっていまして、検索でこのページを
見つけて拝見させていただきました。
実は同本の演習問題にはNO.450とよく似た問題もあり、こちらの方は答えに
対数が出てくるようなのですが、この本には解答がついていません。よろしけれ
ば解き方を教えていただけませんか?
2章 連続確率密度 より
問13
単位長の棒を2本に折り、そのうち長い方を再び2本に折る。(ただし折る箇所
はランダムに選ぶ)このとき出来た3本で三角形が作れる確率を求めよ。
(拙訳をお許しください。原文ものせます。)
(原文)
Take a stick of unit length and break it into two pieces. Choosing the
break point at random. Now break the longer of the two pieces at a
random point. What is the probability that the three pieces can be used
to form a triangle?

| NO.1093 | 2001.11.17. | あみだくじ(5) |
「あみだくじ」の言い出しっぺとしては、
No.1089の水の流れさんの問題に答えないわけにはまいりますまい。
一言でいえば、私がNO.1083で言及した
「バブルソート」をやればよいのです。
|
|
まず、左図1のように、「仮の横線」をひきます。
最初は左端の縦線から始まって、右下がりの階段状に、
右端に達するまで5本の横線をひきます。
その次は、左端から始めてやはり右下がりの階段状に4本、
以下同じ要領で3本、2本、1本とひきます。
こうしてひいた「仮の横線」を上から順に見ていって、
その場所に横線をひくかひかないかを、次のように決定します。
「注目している仮の横線のすぐ上で、
左右の縦線に入ってくる2つの要素の順序(左右)関係が、
くじの下に書かれている要素の順序と逆のときは、その場所に横線をひく。
そうでなければ、その場所には横線をひかない。」
こうすると、上の5本の横線を判定し終えた段階で、
要素 F は必ず右端の縦線にたどり着きます。
右端の縦線には、そこから下に仮の横線は接していないので、
F については目的の位置に到達することが保証されます。
そして、次の4本の横線で E が右から2番目の縦線に送り込まれ、
以下同様に、D, C, B, A もしかるべき位置にたどり着きます。
|
|
これを実際にやってみると、左図2のように、
9本の横線をひくことで、目的のあみだくじができあがります。
この方法による並べ替えの途中経過を観察すると、最も右に来るべき要素が、
「あぶく」のように浮かび上がってくるように見えます。
それゆえ、このアルゴリズムは「バブルソート」と呼ばれています。
ところで、これだけではNo.1089の問題に対する完全な解答にはなっていません。
次のような問題が残っています。
(1) この解は最適解(すなわち、横線の本数が最小の解)であるか?
(2) ((1)が真ならば、さらに)バブルソートは常に最適解を与えるか?
すなわち、任意の要素の並びについて、バブルソートによって得られる解は、
その並べ替えを実現する最適解になっているか?
実は、上の(1)(2)ともに真です。ぜひ証明を考えてください。

| NO.1094 | 2001.11.18. | yokodon | 正(2n+1)角形(2) |
ここでは、複素数 z の共役を z^* で表すことにさせて下さい。
問1:円周上の4点が作る四角形の対角線が直交する条件
4点α、β、γ、δが作る四角形の対角線が直交することは、
arg((α-γ)/(β-δ)) = π/2 …[1]
で表せます。但し、偏角の正方向を反時計回りに取りました。これは、
Re((α-γ)/(β-δ)) = 0 …[2]
と同値です。なぜなら、[1] よりある実数 r が存在して、
(α-γ)/(β-δ) = r・exp(iπ/2)
と表せるため、(α-γ)/(β-δ) は純虚数となるからです。
[2] より、
-(α-γ)/(β-δ) = {(α-γ)/(β-δ)}^*
が成り立ちます。これを変形して、結局以下を得ます。
(α-γ)・(β^*-δ^*) + (α^*-γ^*)・(β-δ) = 0 …[3]
ところで、4点α、β、γ、δは単位円上にあるので、
z^* = 1/z(z = α、β、γ、δ)
が成り立ちます。これを [3] に代入して、
(α-γ)・(1/β-1/δ) + (1/α-1/γ)・(β-δ) = 0
これを整理して、
(α-γ)・(β-δ) ・(αγ+βδ) = 0
を得ます。従って、α、β、γ、δが単位円上の相異4点であることから、目的の式
αγ+βδ = 0 …[4]
を得ます。
問2:正(2n+1)角形の任意の2本の対角線が直交しないこと
件の正多角形の中心を複素平面の原点に取り、正多角形の4頂点を任意に取ってこ
れに反時計回りにα、β、γ、δと名付けたとき、[4] 式が成り立たないことを示せ
ば主張は成立します。なお、回転移動により、α = 1 にすることが出来ます。
このとき、β、γ、δは、以下のように表せます。
β = exp(iu1)、γ = exp(iu2)、δ = exp(iu3)
uk = 2π・jk/(2n+1) 、k = 1,2,3
1 ≦ j1 < j2 < j3 ≦ 2n(各々の jk は整数)
[4] 式に上記を代入して、
exp(iu2) + exp(i[u1 + u3]) = 0
これより、各 uk の値域に注意して以下が成り立つことが分かります。
u1 + u3 = π - u2
これを jk の式に直すと、以下です。
j1 + j2 + j3 = n+1/2
上式を満たす整数の組(j1 , j2 , j3)は明らかに存在しません。
よって、主張は成立です。

| NO.1095 | 2001.11.18. | BossF | 正(2n+1)角形(3) |
問題1
[解](Aと共役なものは~Aと表してます。)
α,β,γ,δは異なる0でない点であるから…(*)
| αγ⊥βδ | |
| ⇔ | (α-γ)/(β-δ)+(~α-~γ)/(~β-~δ)=0 |
| ⇔ | (α-γ)(~β-~δ)+(~α-~γ)(β-δ)=0…① |
| ① | ⇔(α-γ)(1/β-1/δ)+(1/α-1/γ)(β-δ)=0 |
| ⇔(α-γ)(δ-β)/βδ+{(γ-α)/γα}(β-δ)=0 | |
| ⇔(α-γ)(δ-β)(1/βδ+1/γα)=0…② |
問題2
[解]一つの頂点が1であるとしても一般性は失わない
このとき、各頂点は1から左回りにz、z2,z3,…z2nと置ける。
(z2n+1=1である…①ことに注意する)
対角線zp:zqとzr:zs
(p,q,r,sは互いに異なる0以上2n以下の整数)が直交する条件は問題1より
| zp・zq+zr・zs=0 | |
| ⇔ | zp・zq=-zr・zs |
| ⇔ | zp+q-r-s=-1…② |

| NO.1096 | 2001.11.18. | fermeil | 連続の証明(11) |
NO.524 連続の証明(6)連続の証明(6)の記事の下から3行目の f(x)<1/n
はなぜいえるのでしょうか?

| NO.1097 | 2001.11.18. | BossF | 動く楕円(2) |
題意より P(p,0,2) R(x,y,0) と置ける
PR=2√2より
PR2=(p-x)2+y2+22=(2√2)2
i.e.(p-x)2+y2=4…①
ここで、P、Q、Rのz座標より
QがP、Rの中点であることに注意すると
q=(p+x)/2⇔p=2q-x…②
②を①に代入して整理し
(x-q)2+(y2)/4=1…③
③はqが-1≦q≦1の範囲で動くとき
x2+(y2)/4=1
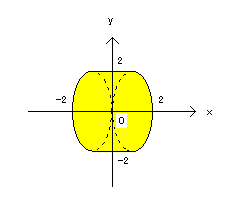
がx軸方向に l1l の範囲で平行移動することを示すから
求める図は下図

| NO.1098 | 2001.11.18. | 水の流れ | 三角形可能な確率(4) |
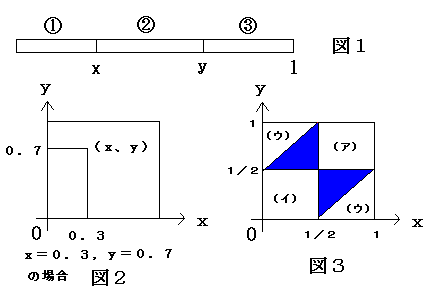
棒の長さを1とする。棒を左右に置いて、左端を0,右端の点を1とする。そして、
2カ所の切断点の、0(左端)からの距離を、x、yとし(ただし、x、yの大小の
区別をつけない)、出来た3本の辺を、(x、yの大小に関わらず)左から①、②、
③とする。(図1参照)
そして、さっきと同様、2数x、yを点(x、y)で表し、0≦x≦1,0≦y≦
1の座標を考える。(図2参照)
三角形ができるためには、「どの1辺も他の2辺の和より短い。」
今、3辺の和が1だから、このことを言い換えると、
「どの辺も1/2より短くなければならない。」
ここでは、逆に、三角形が出来ない場合を考える。
まず、①が1/2より大きくなる場合。
このとき、x、yはともに1/2より大きいから、1/2≦x≦1、1/2≦y≦1。
これは図3の(ア)の部分になる。
次に、③が1/2より大きくなる場合も同様で、x、yはともに1/2より小さくな
るから、0≦x≦1/2,0≦y≦1/2。これは図3の(イ)の部分になる。
最後に、②が1/2より大きくなるのは、x、yの差が1/2より大きくなるとき
がから、|x-y|≧1/2。これは図3の(ウ)の部分になる。
したがって、三角形が作れるのは、(ア)、(イ)、(ウ)を除いた青い部分で、
その面積は、正方形全体の1/4になる。
よって、求める面積は、1/4である。
<解答の出典:算数はアタマのよくなるパズルだ:みくに出版>:(コメント:一
部、記号を変更し、詳しくしてある。)

 E-mail
E-mail
 戻る
戻る