
Weekend Mathematics/コロキウム室/NO.124
| NO.1055 | 2001.10.7. | BossF | できるでしょうか? つづき(2) |
何か条件が抜けてませんか?
7cm×7cmの正方形の内部に直径1.5cmの円を描きその内部に50個の点を適当にとれ
ば、どの2点の距離も1.5cmより短くなってしまいます…
そんな問題ではないと思うのですが?

| NO.1056 | 2001.10.7. | やなせ | 魔法陣(1) |
簡単に誰でも出来る奇数の魔法陣(幾つになってもね)の解き方を紹介します。
魔法陣の外に架空の升目を想定します。
その上で表のように数字を書き込んで架空の升目に入った数字を移動します。
(わかりにくいかな?)
同じように1.2.3はそのまま下の方の連続斜め3マスの所に
5.6.7.は横に8.9も下の方の連続斜め2マスに…
こんなふうにすれば奇数については魔法陣を解くことが出来ます。
7でやってみました
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
偶数の場合は4でいきますが
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
一応このように入れます、次に4隅と対角の数字は固定します。
つまり1.4.6.7.10.11.13.16です。
残った数字を升目の中心を芯として(苦しい表現)入れ替えます。
| 1 | 15 | 14 | 4 |
| 12 | 6 | 7 | 9 |
| 8 | 10 | 11 | 5 |
| 13 | 3 | 2 | 16 |

| NO.1057 | 2001.10.7. | yokodon | 素因数分解を一部用いて定義される数列 |
模試シリーズ5
自然数 n の素因数分解を行って、n = 2a・b(a 、b はある整数)
と表せるとき、b = f(n) とおく。
また、m を自然数として、
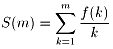
とする。

| NO.1058 | 2001.10.8. | BossF | 素数の問題・その2おまけの問題 |
素数の問題・その2より、
「自然数aとbをとるとき、a3+b3+4はある自然数の3乗とはならないことを
示しなさい。」
[解]
任意の整数 n は,n≡0,±1(mod3)のいずれかを満たす。
ここで、
n≡0(mod3) ⇒n3≡0(mod9)
n≡±1(mod3)⇒n3≡±1(mod9)だから、
任意の整数 n について n3≡0,±1(mod9)…①
さて①より、任意の整数 a , b について
a3+b3≡0,±1,±2(mod9)
すなわち、a3+b3+4≡2,±3,±4(mod9)…②
①②より題意は示された■
丁寧にやるなら次の補題を示すのでしょうね。
[補題]
n≡0(mod3) ⇒n3≡0(mod9)
n≡±1(mod3)⇒n3≡±1(mod9)
<補題の証明>
n=3k ⇒n3=27k3=9・3k3≡0(mod9)
n=3k±1⇒n3=(3k±1)3
=27k3±27k2+9k±1
=9(3k3±3k2+k)±1≡±1(mod9)

| NO.1059 | 2001.10.8. | DDT | 微分(5) |
NO.1011 微分(4) yokodonさん の真意を理解するのに、しばらくかかりました。
あくまで私なりの理解ですけど・・・。とりあえず、わかったことを・・・。
関数f:R → Rが一点xで、収束半径ρのもとに展開半径|h0|<ρでテーラー展開可能とします。
それをf(j)(x)=ajと書くことにして、
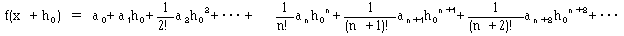
(1)
とします。いっぽう式(1)のn次までのテーラー近似は、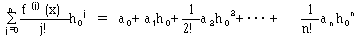
(2)
です。よって、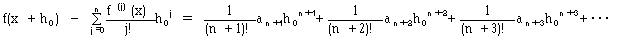
(3)
です。式(3)にコーシーの平均値定理を使います。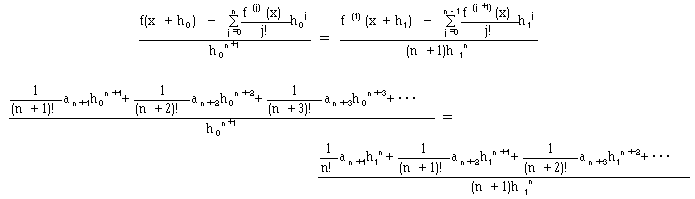
となる0<|h1|<|h0|が存在する.
(4)
ここで0<|h1|<|h0|<1とします。 すると、次数の少ない項ほど効いてくるので式(4)は、高次の項を無視して、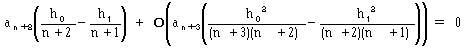
(5)
と整理できます。ここでOは、ランダウ記号(ちょっと使い方が違いますか?)。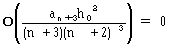
(6)
しか残らず、じゅうぶん小さなh0とじゅうぶん大きなnに対して、h1=h0・(n+1)/(n+2)は非常に 良いh1の近近似を与えることがわかります。式(4)にコーシーの平均値定理を使いつづけ、最終的に、
(7)
の形を得た場合、同じことをn回繰返すので、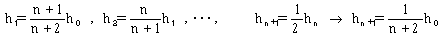
(8)
となります。従って、f(x+h0)にふつうの平均値定理を繰り返し用いて得た結果、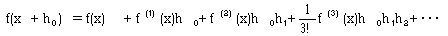
にh1=h0/2,h2=h0/3,・・・を使い、
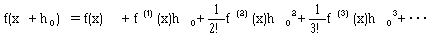
とすることは、f(x+h0)に対するかなり良い近似値を与えることになります
(それはそうですね)。
ところで式(7)の最左辺と最右辺を直接等置した式を、式(1)でベキの形に書き変えれば、
hn+1とh0の関係を直接導けるはずです。実際にやってみると、
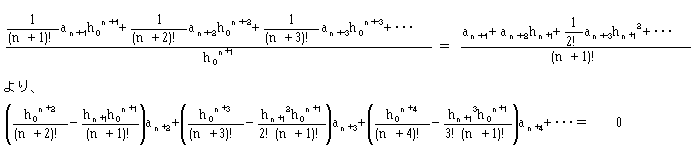
(9)
が得られます。ここでhn+1のh0/(n+2)からのずれを計算するために、 hn+1=h0(1+ε)/(n+2)とおき、式(9)に代入してみます。 εはいわゆる誤差です。結果として、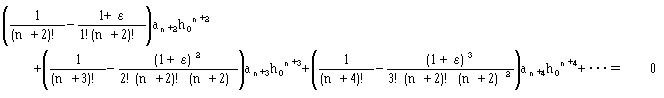
(10)
が得られます。式(10)の左辺全体をRn(ε)とおきます。
(11)
次にRn(ε)の有限部分和をRn,mとし、 ρn,m-1=Max({|an+j+2/(n+j+2)!|1/(n+j+2)} j=0~m)と定義します。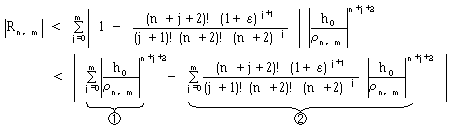
(12)
となります。ただし式(12)では、(13)
を仮定しています。式(12)の項①と②を別々に評価します。(14)
とすると、(15)
でもあるので、収束半径ρに関して、(16)
です。よって、じゅうぶん大きなnに対してρn,mは、いくらでもρに近づけます。(17)
も成り立ちます。従って、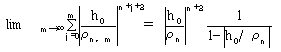
(18)
②: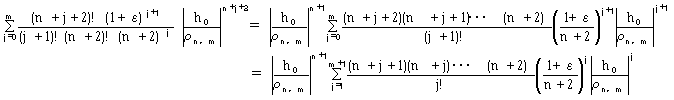
(19)
と変形できます。 式(19)の下段のΣ内は、ちょうど(1-x)-n-2のマクローリン展開 (から初項を落としたもの)の形をしています。その収束半径は、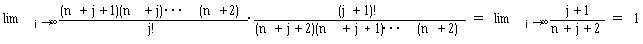
(20)
hn+1=h0(1+ε)/(n+2)の定義から0<h0(1+ε)/(n+2) <h0で、0<(1+ε)/(n+2)<1。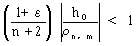
(21)
となり、式(19)のΣでm→∞としたものは、じゅうぶん大きなnについてベキ級数として収束します。 従って、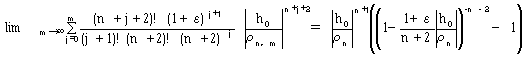
(22)
です。式(11),(12),(18),(22)より、じゅうぶん大きなnに対して、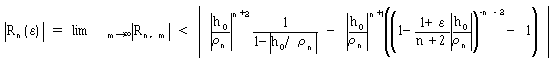
(23)
が得られます。以上の結果より、次の定理(?)となります。 定理(?)
関数f:R → Rが一点xで、収束半径ρのもとに展開半径|h0|<ρで
テーラー展開可能とする。このとき、

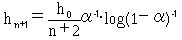
(24)
を満たす。ただしα=|h0/ρ|で、上式はα→0で、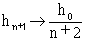
(25)
の極限を持つ。特に収束半径ρ=∞のときは、じゅうぶん大きなnについて常に、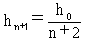
(26)
として良い。α=|h0/ρ|が1に近づくに従い、 式(24)の収束性は悪い(式(24)より明らか)。[証明]
テーラー展開可能な関数のテーラー級数をベキ級数と考えた場合、
項別の微分と項別の演算が可能で、微分した結果はもとと同じ収束半径を持つので、
式(9)より式(11)が得られる。
Rn(ε)=0とすれば、
hn+1=h0(1+ε)/(n+2)のh0/(n+2)からのずれである
εを求められる。式(23)より、じゅうぶん大きなnに対して、
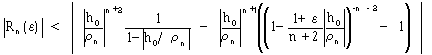
(27)
が成り立つ。式(27)の右辺が0であれば、Rn(ε)=0は明らかだから、 式(27)の右辺を0とするεを求める。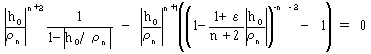
(28)
より、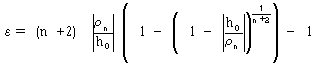
(29)
式(29)のn→∞での極限値はロピタルの定理より、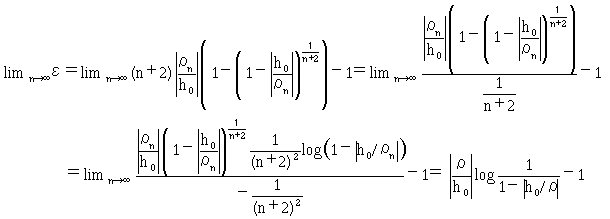
(30)
となる。式(30)の末項に注意し、α=|h0/ρ|として、 ε=ε(α)とおけば、ε(α)はじゅうぶん大きなnとα→0に対して次の極限値を持つ。 再びロピタルの定理から、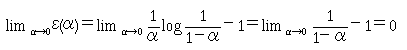
(31)
[証明終わり] ところでyokodonさんは次のように仰いました。
① f(x+h0) の展開式で、
数列{hn}を以下を満たすようにとります。
hn=h0/(n+1) n=1,2,...
このとき、
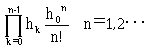


| NO.1060 | 2001.10.9. | やなせ | 魔法陣(2) |
魔法陣8です。
なにせ古い記憶を頼りですので(笑)
解答はこちら
| 1 | 56 | 43 | 25 | 33 | 24 | 16 | 57 |
| 63 | 10 | 18 | 39 | 31 | 42 | 50 | 7 |
| 62 | 11 | 19 | 38 | 30 | 43 | 51 | 6 |
| 4 | 53 | 45 | 28 | 36 | 21 | 13 | 60 |
| 5 | 52 | 44 | 29 | 37 | 20 | 12 | 61 |
| 59 | 14 | 22 | 35 | 27 | 46 | 54 | 3 |
| 58 | 15 | 23 | 34 | 26 | 47 | 55 | 2 |
| 8 | 49 | 41 | 32 | 40 | 17 | 9 | 64 |
4の時と同じ法則で移動するのですが
残す数値は下記のようになります
○はそのまんま、×は移動
| ○ | × | × | ○ | ○ | × | × | ○ |
| × | ○ | ○ | × | × | ○ | ○ | × |
| × | ○ | ○ | × | × | ○ | ○ | × |
| ○ | × | × | ○ | ○ | × | × | ○ |
| ○ | × | × | ○ | ○ | × | × | ○ |
| × | ○ | ○ | × | × | ○ | ○ | × |
| × | ○ | ○ | × | × | ○ | ○ | × |
| ○ | × | × | ○ | ○ | × | × | ○ |

| NO.1061 | 2001.10.9. | Hakuchonn | 最近考えていた問題 |
最近考えていた問題を何題か紹介したいと思います。
①有名題です。三角形ABCが与えられていて、ABCの内接円の半径をr,外接円
の半径をRとする。
このとき、R≧2r となることを示せ。
②a,b,c>0のとき、
(1/a)+(1/b)+(1/c)≦1/(a+b-c)+1/(c+a-b)+1/(b+c-a)
となることを示せ。
③三角形ABCの内部の点Pで、
PA+PB+PC が最大となるようなものを見つけよ。
④ABCDは∠A=60°であるような菱形である。
点E,Fをそれぞれ辺AB,AD上の点とし、CE,CFはBDとそれぞれP,Qで交わる。
また、(BE)2+(DF)2=(EF)2 が成り立っているとき、
(BP)2+(DQ)2=(PQ)2 を証明せよ。
⑤(代数を2つ)
(1) pを素数とする。2/a+3/b=5/p の正整数解を全て見つけよ。
(2) 任意のXについて、
(x-1)2{P(x)}=(x-3)3{P(x+2)}
を満たす実係数多項式P(x)を全て求めよ。
問題の出典を書いておきます。
②:ポーランド数オリ、1次
④:清宮俊雄氏による問題です
③、⑤は人から聞いた問題ですが、カナダの雑誌に載っていたそうです。

| NO.1062 | 2001.10.9. | Hakuchonn | できるでしょうか? つづき(3) |
コロキウム室 NO.1050 「できるでしょうか? つづき」
、正しくは、
「問題:
7×7のボードに50個の点を打つとき、どのように打っても必ず距離が1.5未満であ る2点が存在することを示せ。」
上のような問題を紹介しておきます。
①A君は55冊の漫画を1日1冊、合計31日で読みました。このとき、ある連続し
た何日かで丁度25冊を読んでいることを示して下さい。
②長さ1の線分上にあるいくつかの小区間を赤色で塗る。どの赤色の2点間の距離も
0.1ではないとする。このとき赤い区間の長さの総和は0.5以下であることを証明せよ。

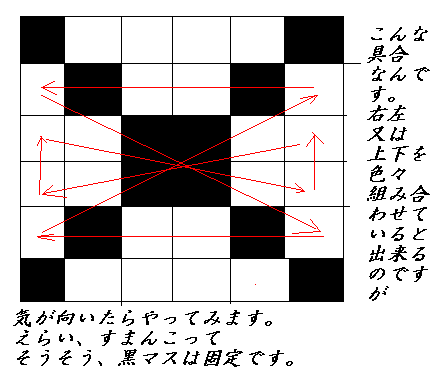
| NO.1063 | 2001.10.10. | やなせ | 魔法陣(3) |
6の魔法陣も考えようと思っているのですが
何せ、水平移動と、対角移動、垂直移動と対角移動が関係していたように
思うので、なかなかですハイ!
固定するところは、対角の11個の数字なのは、解っているのですが・・
BMPでヒントだけ(儂にもこたえおしえてぇ~~)を
送っておきます。

 E-mail
E-mail
 戻る
戻る